
Джон Мичелл
(1863–1940)
Ада Шоломовна Готман,
д.т.н., профессор кафедры теории и устройства корабля
Новосибирской государственной академии водного транспорта
Очарование,
которым обладает наука,
позволяет нам преодолеть естественное отвращение ко всякому напряжению ума.
Гаспар Монж
Определение сопротивления воды движению судна - одна из самых удивительных по простоте постановки и трудности решения проблем. Её изучение потребовало огромного напряжения ума многих учёных в течение последних столетий. История этой проблемы украшена замечательными именами и замечательными идеями.
Полное сопротивление воды движению судна - это сумма гидродинамических сил, действующих со стороны жидкости на смоченную поверхность корпуса. Часть этих сил зависит от вязких свойств жидкости, создавая сопротивление трения и турбулентный попутный поток. Часть сил связана с гравитацией и даёт волновую составляющую сопротивления, создавая вокруг судна две системы волн, каждая из которых заключена в своём полубесконечном клине. Вершина одного клина находится в носу судна, а вершина второго - в корме; и обе волновые системы, как приклеенные, движутся вместе с судном.
При проектировании корпуса судна необходимо решить два вопроса. Первый связан с возможно более точной оценкой полного сопротивления судна с заданной формой корпуса. Для этого используются расчётные методы и модельные испытания в опытовом бассейне. Второй вопрос – это поиск формы обводов с наименьшим сопротивлением воды. Для решения этой задачи проводятся испытания серии моделей судов с разными обводами корпуса. Расчетные методы в этом случае дают только направление, в котором нужно менять форму корпуса, чтобы получить наименьшее сопротивление.
Одним из самых поразительных исторических событий была организация в середине двадцатого века – века холодных и мировых войн международного сообщества учёных для решения проблемы определения сопротивления воды движению судна.
Несмотря на то, что люди строят суда тысячи лет, вопрос о расчёте сопротивления корпуса при его движении практически возник только тогда, когда вместо парусов и рабов на судно поставили двигатель. Для того чтобы посчитать скорость, которую может обеспечить данный двигатель, нужно посчитать сопротивление воды. Но ещё до появления двигателей делались попытки научно подойти к изучению движения судов. Первый пароход Фултон построил в 1807 году, а самый первый труд, посвященный описанию движения тел в воде, был написан ещё Леонардо да Винчи (1458-1519) и назывался«О движении и измерении воды», но опубликовали его только через 300 лет.
Интересно проследить за развитием идей, связанных с определением сопротивления воды движению судна.
1687 год – Исаак Ньютон(Англия) впервые попытался создать теорию сопротивления воды движению тел в жидкой среде, которую опубликовал в труде«Математические начала натуральной философии». Его формула квадратичного закона зависимости сопротивления от скорости явилась большим научным открытием того времени. И совершенно замечательной оказалась формула Ньютона о связи касательных напряжений в жидкости с динамическим коэффициентом её вязкости и градиентом скорости. Эта формула Ньютона используется в гидродинамике не меньше, чем его законы в механике.
1746 год – П. Буге (Париж) написал «Трактат о корабле, о его конструкции и его движении».
1749 год – Леонард Эйлер (Россия) написал монографию «Корабельная наука», а в 1778 году – «Полное умозрение строения и вождения кораблей». Взамен теории ударов Ньютона Эйлер разработал теорию обтекания и даже получил формулу зависимости сопротивления воды от площади миделя, удлинения корпуса судна, плотности жидкости и квадрата скорости его движения.
1756 год – Бэрд (Англия) впервые провёл испытания моделей судов в опытовом бассейне длиной10 метров.
1775 год – Ж.Л. Д’Аламбер, Э. Боссю, М.Ж.А. Кондорсе(Франция) провели первые систематические сравнительные испытания моделей судов в бассейне гравитационного типа с определением сопротивления воды.
1871 год – Вильям Фруд (Торквей, Англия) построил первый бассейн с тележкой, а в 1873 году он разработал метод пересчёта сопротивления с модели на натуру, пользуясь законом гравитационного подобия, идея которого принадлежит Реху (1844).
Фруд впервые предложил научный метод пересчёта на натуру результатов измерений, полученных на моделях в бассейне. Метод Фруда является одним из самых замечательных по своей практичности. Для выделения сопротивления трения Фруд высказал замечательную идею об эквивалентных досках. Проводятся буксировочные испытания тонких досок, площадь которых равна площади смоченной поверхности корпуса судна, а потом их сопротивление вычитается из полного сопротивления судна. Таким путём получается остаточное сопротивление, которое пересчитывается на натуру по закону подобия Фруда. Кроме того, Фруд получил критерий подобия гравитационных сил модели и судна, который называется числом Фруда. Экспериментальная теория Фруда до сих пор сохраняет своё преимущественное значение, потому что приближения теории всё ещё менее точны, чем эксперименты.
1880 год – Д.И. Менделеев(Россия) опубликовал работу «О сопротивлении жидкостей и о воздухоплавании». Он изложил основы учения того времени о сопротивлении трения и указал на необходимость связи теории и опыта. По его инициативе и поддержке в Петербурге был построен первый в России опытовый бассейн, носящий его имя и действующий поныне. Первыми научными руководителями этого бассейна были А.Н.Крылов и И.Г. Бубнов, которые старались применять теорию одновременно с экспериментальными исследованиями. Под руководством акад. А.Н. Крылова сформировалась школа русских учёных-кораблестроителей, отличительной чертой которой является доведение теоретических выводов до практических средств инженерного расчёта. Эта тенденция является традиционной в отечественной науке. После смерти А.Н. Крылова почти ежегодно проводятся Крыловские чтения, на которых обсуждаются последние теоретические и экспериментальные достижения.
1883 год – Осборн Рейнольдс (Англия) получил безразмерный критерий подобия потоков вязкой жидкости, который называется числом Рейнольдса. При пересчёте результатов модельных испытаний на натуру число Рейнольдса необходимо так же, как и число Фруда. Число Рейнольдса – это тоже замечательная практическая идея в области определения сопротивления воды движению судов. Александр Гюстав Эйфель(Франция) нашёл критическое число Рейнольдса, при котором происходит переход ламинарного режима течения к турбулентному.
1887 год – Лорд Кельвин – Томсон (Англия) теоретически решил задачу о корабельных волнах от движущегося импульса давления, используя теорию бесконечно малых волн. Он впервые получил значение 38°56′ – угла клина, внутри которого наблюдаются корабельные волны, знакомые любому, кто видел движение какой-нибудь лодки или судна.
1898 год – Джон Генри Мичелл впервые разработал линейную теорию волнового сопротивления судна и получил формулу для волнового сопротивления узкого судна при движении по поверхности идеальной жидкости бесконечной глубины. Мичелл установил зависимость волнового сопротивления судна от уравнения поверхности корпуса, выразив её в виде интеграла, который носит его имя. Эта фундаментальная работа оказалась незамеченной в течение почти тридцати лет. Объяснить это можно только тем, что Мичелл не привёл результатов расчётов, хотя он, по свидетельству его брата (также почётного члена английского Королевского Научного общества), выполнил их для большого количества реальных судов.
Эта замечательная работа Мичелла в области определения сопротивления воды движению судна не потеряла своего значения и по сей день. Интеграл Мичелла играет не меньшую практическую роль, чем метод Фруда и труды Рейнольдса.
Итак, девятнадцатый век закончился получением теоретического решения задачи о волновом сопротивлении судна в точной линейной постановке.
Двадцатый век начался с попыток решать задачи с учётом вязкости жидкости.
1904 год – Людвиг Прандтль(Германия) разработал теорию пограничного слоя, которая оказалась исключительно плодотворной как с практической, так и теоретической точки зрения.
 Джон Мичелл (1863–1940) |
В середине двадцатых годов В. Виглей в Англии и Г. Вейнблюм в Германии обратили внимание на работу Мичелла. Они разработали большие серии моделей с аналитически заданными обводами, что позволило достаточно точно считать интеграл Мичелла и сравнивать результаты расчётов с данными экспериментов. Выяснилось, что интеграл Мичелла даёт хороший качественный результат, особенно, когда модели отвечают условиям Мичелла. Условия были следующие: во-первых, отношение ширины корпуса к его длине должно быть малым; во-вторых, осадка должна быть большой. Серийные испытания Виглея и Вейнблюма позволили достаточно полно изучить интеграл Мичелла и использовать его для разных форм корпуса. Типичные результаты расчётов показаны на рис. 1, откуда видно, что интеграл Мичелла даёт хороший качественный результат, но расчётная кривая имеет горбы и впадины, которых никогда не бывает на экспериментальных кривых.
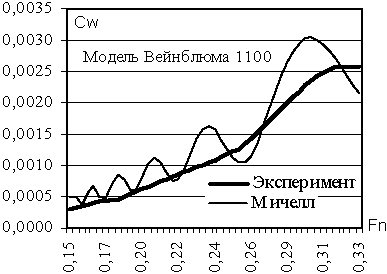
Рис. 1. Типичное соотношение между расчетной кривой Мичелла и экспериментальной кривой остаточного сопротивления.
 В. Виглей (1890-1970) |
Виглей и Вейнблюм объясняли наличие отражения. Для того, чтобы исключить влияние горбов и впадин на расчётной кривой волнового свободной поверхности и корабельных волн, сопротивления тем, что интеграл Мичелла получен без учёта вязкости жидкости. Для определения области применимости интеграла Мичелла Вейнблюм и др. провели испытания модели, которую они назвали «шероховатой пластиной» с отношением длины к ширине 37,67. Оказалось, что при числе Фруда больше 0,2 расчётные горбы и впадины совпадают с полученными в эксперименте. В 1969 году С. Шарма провёл в Гамбурге подобные испытания модели с относительным удлинением, равным 20. Экспериментальная кривая совпала с расчётной кривой Мичелла при числах Фруда больше 0,3. Т. Хавелок (1935) и В. Виглей(1937–38) пытались привести в соответствие расчётные и экспериментальные кривые волнового сопротивления для моделей судов разной формы с помощью введения в формулу Мичелла поправочных коэффициентов. Для того, чтобы разработать практически полезную теорию определения волнового сопротивления, необходимо было не только понять причины расхождений между теорией и экспериментом, но и найти способы экспериментального выделения волнового сопротивления из полного.
1924 год – Г. Фёттингер реализовал высказанную им ещё в1903 году идею использования дублированной модели для разделения вязкостного и волнового сопротивления. Дублированная модель – это соединённые по плоскости действующей ватерлинии поверхности подводной части корпуса судна и её зеркального дублированную модель испытывают либо глубоко под поверхностью жидкости в опытовом бассейне, либо в аэродинамической трубе. Таким путём получают сопротивление трения плюс сопротивление формы. При движении модели по поверхности жидкости получают полное сопротивление в виде суммы составляющих трения, формы и волнового. Г. Фёттингер не только предложил эту замечательную идею, но разработал метод пересчёта на натуру результатов испытаний модели в аэродинамической трубе, используя число Рейнольдса в качестве критерия подобия.
Использование дублированной модели - это второй шаг после Фруда в развитии экспериментальных способов определения составляющих полного сопротивления.
Т. Хавелок выполнил ряд теоретических работ, в которых дублированная модель используется в теории волнового сопротивления и волнообразования для описания поверхности корпуса с помощью гидродинамических особенностей. И если дублированная модель для экспериментов – это реальное физическое тело, то в расчётах – это воображаемая замкнутая поверхность, по которой распределены гидродинамические особенности в виде источников, диполей или вихрей. Моделирование поверхности судна с помощью дублированной модели широко используется в современных численных методах определения сопротивления движению судна.
 Т. Инуи |
1960 год – впервые в работе бассейнов начинают использовать методы, который называют – «анализом волнообразования», «волновым анализом» и «обследованием попутного потока». Если Фруд и его последователи занимались, в основном, замерами сил, то в Японии начались интенсивные наблюдения за волновой картиной. Количественное измерение параметров волн для определения волнового сопротивления – замечательная идея. Конечно, наблюдения за волнообразованием велись всегда, но использовали картину волнообразования для количественной, а не качественной, оценки сопротивления только в шестидесятые годы прошлого столетия. Для этого пришлось использовать компьютерную технику и стерео – фотографирование. Кроме волн замеряется потеря количества движения для оценки вязкостного сопротивления судна.
 Л. Докторс |
С 1908 Т. Хавелок (Англия) опубликовал около 40 статей по волнам и волновому сопротивлению, которые стали базой для дальнейшей работы в этой области.
 Е. Так |
В тридцатые годы прошлого столетия русские учёные Л.Н. Сретенский, Н.Е. Кочин, И.Г. Ханович и Л.И. Седов интенсивно изучали решение Мичелла. Тогда же Н.Е. Кочин получил решение, подобное интегралу Мичелла. Для упрощения расчётов Кочин протабулировал функцию, которая носит его имя и широко используется во всём мире. Во второй половине двадцатого века линейной теорией волнового сопротивления занимались крупные учёные разных стран: Дж. Лунде (Норвегия), Дж. Ньюман (США), Б. Андерссон (Швеция), Т. Инуи, Е. Баба, Х. Маруо и М. Бесшо (Япония), Е. Так и Л. Докторс (Австралия), К. Эггерс (Германия) и др.
В начале шестидесятых годов Г. Воссерс и Е. Так попытались применить модель, так называемого, удлинённого тела для судов. В этом случае у судна не только ширина, но и осадка принимается малой. Эта идея казалась привлекательной с точки зрения упрощения теоретического решения задачи.
 Ф. Ноблесс |
Среди перечисленных замечательных имён Е. Так занимает достойное место, решив к настоящему времени сотни задач из области корабельной гидродинамики. Не менее плодотворно работают сейчас Дж. Ньюман (США), Ф. Ноблесс (Франция) и Л. Докторс (Австралия). Список научных публикаций, каждого из них длиннее этой статьи.
 Дж. Ньюман |
Внимание учёных к линейным теориям вполне понятно. Обычно в любых инженерных расчетах ограничиваются решением первого порядка, потому что при этом получают главную часть искомой величины. Линейная теория Мичелла подтверждает это положение. И всё было бы хорошо, если бы интеграл Мичелла можно было использовать для вычисления волнового сопротивления реальных судов. Дело не только в горбах и впадинах, отражающих взаимодействие кормовой и носовой волновых систем судна в идеальной жидкости. Эти линейные теории нельзя использовать для широких судов типа речных, судов прибрежного плавания, рыболовных и т.п., так как одним из допущений, позволивших Мичеллу получить решение задачи, было условие малого отношения ширины корпуса к его длине.
 Г. Вейнблюм (1897–1974) |
Упорные исследования продолжались во многих опытовых бассейнах СССР, Франции, Швеции, Германии, Англии, США, Японии. В 1956 году в Вашингтоне состоялся первый Международный Симпозиум по гидродинамике морских судов (Symposium on Naval Hydrodynamics). С тех пор каждые два года вновь собираются на этот симпозиум специалисты всех континентов. Результаты исследований публикуются не только в трудах симпозиума, но и в научных журналах. Надо отметить большую роль издающегося с1957 года американского журнала Journal of Ship Research, а также журнала по механике жидкости Fluid Mechanics. До начала шестидесятых годов, в основном, в них публиковались результаты систематических серийных испытаний моделей судов разного типа. Причем, при проведении этих испытаний теория использовалась очень мало. Научная мысль получила сильный толчок в1963 году. К этому времени резко повысились мировые цены на топливо, и судовладельцы и судостроители заинтересовались возможностью повысить ходовые качества судов за счёт улучшения форм корпуса судна. Снизить сопротивление морских судов стало насущной необходимостью. Большую роль в организации работы по расчётам волнового сопротивления и по выбору обводов с наименьшим сопротивлением сыграл замечательный учёный Георг Вейнблюм. Именно по его инициативе возникло то мировое сообщество, которое все усилия направило к решению упомянутых выше задач. Это сообщество состоит из крупных учёных, и стоит того, чтобы войти в историю мировой науки, как замечательное явление. Эта статья стимулирована успехами работы именно этого международного сообщества.
Г. Вейнблюм, работая в Опытовом Бассейне Давида Тейлора в Вашингтоне, содействовал созданию Американской школы корабельной гидродинамики, в которую привлёк математиков Л. Ландвебера, Ф. Михельсена, М. Тулина, Дж. Вехаузена, Ф Урселла, К. Эггерса, Ф. Ноблесса, Г. Дагана и др. Вейнблюм говорил, что для решения задачи о сопротивлении воды движению судов необходимы«не судостроители, физики, гидромеханики, а математики», потому что, по его словам, «теория судна слишком трудна для инженеров». В 1952 году Вейнблюм стал директором вновь основанного Института Кораблестроения в Гамбургском Университете. Этот институт и по сей день привлекает к научной работе талантливых учёных.
 В.Г. Сизов |
В то же самое время, а именно в1959 году, в Японии был организован «домашний симпозиум», для сотрудников научно-исследовательских институтов, профессоров университетов, судостроительных институтов и аспирантов. Время показало, что эти объединенные усилия дают хорошие результаты.
1961 год - В.Г. Сизов (Одесса) впервые решил задачу определения волнового сопротивления судна с учётом нелинейных эффектов. Это первенство и по сей день отмечается во всех работах, посвящённых волновому сопротивлению судна.
1962 год – Дж. Хесс и А. Смит разработали численный метод определения поля скоростей и давлений вокруг полностью погруженного тела произвольной формы. Это был важный шаг в истории развития численных методов в гидродинамике судна.
 А.А. Костюков (1909-1976) |
Г. Вейнблюм совместно с Р. Кохом решили организовать Международный Семинар по теоретическому и экспериментальному определению волнового сопротивлению, который и состоялся в Анн Арборе при Мичиганском Университете в августе в1963 года. На семинар было представлено 39 работ (на 1352 стр.). От СССР лично никто не присутствовал, но обсуждалась вышедшая в 1959 году книга А.А. Костюкова «Теория корабельных волн и волнового сопротивления».
 Джон Вехаузен |
На Анн Арборском семинаре дебютировала группа учёных из Японии Т. Инуи (Токио), М. Бесшо (Иокогама), Х. Маруо (Иокогама) и Х. Кайитани (Токио), которым была для этого оказана финансовая поддержка, и которые в дальнейшем стали замечательными участниками работы этого сообщества.
Большую роль в организации Анн Арборского семинара играл профессор Дж. Вехаузен. Блестящий математик, знающий почти все европейские языки, а также русский и турецкий, он смог быстро составить большую библиографию работ по поверхностным волнам, по волновому и вязкостному сопротивлению судов на глубокой и мелкой воде и в двухслойной жидкости. Эта библиография помогала и сейчас помогает ученым знакомиться с работами, выполненными в разных странах. Вехаузен (совместно с Лайтоне) написал в 1960 году энциклопедический труд по поверхностным волнам, до сих пор не потерявший своей актуальности, и в настоящее время заботами его коллег записанный на сайте в Интернете. Но Вехаузен занимался не только составлением аналитических обзоров и библиографий. Он получил фундаментальные решения задачи о волновом сопротивлении в нелинейной постановке по методу Эйлера и Лагранжа. Великолепный педагог – он воспитал прекрасных учёных. Говоря о Вехаузене, невозможно не сказать о его личной скромности и обаянии, которые отмечаются всеми, кто имел счастье общаться с этим замечательным человеком.

Участники семинара в Анн Арборе в августе 1963 года
Сидят (справа налево) К. Эггерс, С. Шор, Т. Инуи, Дж. Вехаузен, Л. Ландвебер, Г. Вейнблюм, Р. Кох, Ф. Урселл (третий слева), Р. Тимман
Вейнблюм, Вехаузен, Брар, Эггерс, Бесшо, Маруо, Инуи не только определили высокий математический уровень теоретических работ в области волнового сопротивления, но создали доброжелательную атмосферу взаимопомощи и поддержки в процессе работы. Сложилась прекрасная традиция обмена(до опубликования) полученными результатами и практика проверки теоретических работ. Установление дружеских отношений внутри этого мирового сообщества стало непременным условием совместной работы.

К. Эггерс, А.Гамст, Т. Инуи, Дж.Вехаузен, Х Кайитани (сидит), К.Накатаке, Т.Милох, С. Шарма
 Роже Брар (1907-1977) |
На семинаре в Анн Арборе был выбран Международный Комитет опытовых бассейнов во главе с академиком, вице-адмиралом Роже Браром. На семинаре, в основном, обсуждались расхождения между теорией и экспериментом. В результате работы семинара были определены следующие задачи: 1) найти пути улучшения линейной теории Мичелла, которая позволяет искать формы корпуса судна с наименьшим волновым сопротивлением; 2) найти пути решения задачи в нелинейной постановке, то есть, точной задачи движения судна с постоянной скоростью по поверхности идеальной жидкости; 3) найти пути экспериментального определения волнового сопротивления вместо остаточного, которое определяется по закону Фруда; 4) выявить причины слишком резко выраженных горбов и впадин на теоретической кривой волнового сопротивления; 5) найти теоретические возможности определения волнового сопротивления при движении судна в вязкой жидкости.
 Клаус Эггерс |
В Анн Арборе обсуждались методы определения волнового сопротивления по замерам волн. Были предложены несколько методов для таких измерений. Благодаря хорошим контактам с Американским Бюро Военно-морских исследований и большому личному обаянию, Вейнблюм дал начало многим международным встречам, симпозиумам и семинарам. Клаус Эггерс, один из ведущих учёных Германии в области гидромеханики судов, выполнил ряд экспериментальных и теоретических исследований волнового сопротивления. Нужно отметить личное обаяние Клауса Эггерса, благодаря которому Вейнблюм поручил ему поддерживать связь с учёными Востока. В частности, он постарался облегчить японским учёным участие в Анн Арборском семинаре. В то время японские ученые плохо владели английским языком.
Если до этого знаменитого семинара публиковалось всего несколько работ о волновом сопротивлении в год, то после него решения появлялись десятками и сотнями.
Научные статьи, и отчёты начали появляться сотнями. Казалось, что ознакомиться со всеми работами совершенно невозможно. Особенно трудно было учёным в СССР из-за отсутствия необходимых журналов и материалов симпозиумов. Но время от времени появлялись хорошие обзоры. Здесь следует выделить книжку Дж. Вехаузена (1973) по волновому сопротивлению судов. Эта обзорная работа по сопротивлению в силу своей глубины не теряет актуальности и поныне. Кроме того, ситуация несколько облегчалась тем, что в то время требовалось каждую статью начинать с краткого обзора и анализа предшествующих работ.
 М. Бесшо |
М. Бесшо (период 1960–76, Иокогама) сделал ряд важных теоретических работ. После Анн Арборского семинара были осуществлены теоретические работы по нелинейным теориям волнового сопротивления. М. Икехата (1965, Кавасаки), К. Эггерс (1966, Гамбург), Х. Маруо (1966, Иокогама), Б. Йим (1968, США) и Дж. Вехаузен (1969, Беркли) сделали фундаментальные работы по теории волнового сопротивления второго порядка с разными граничными условиями.
1969 год – Е. Баба обнаружил в процессе теоретического и экспериментального изучения полного сопротивления судна новую вязкостную составляющую. При определении потери общего напора, появилась дополнительная потеря количества движения вне попутного потока. Предварительные теоретические исследования этой составляющие показали, что она подчиняется закону подобия Фруда, несмотря на то, что обнаруживается при изучении попутного потока. Эта составляющая позволила объяснить, почему волновое сопротивление, полученное с помощью техники волнового анализа, оказалось слишком маленьким по сравнению с разностью полного и вязкостного сопротивления.
 Е. Баба |
1975 год – Е. Баба и К. Такекума разработали новую нелинейную теорию, так называемую, теорию малой скорости, которая явилась большим шагом вперёд после долгого периода мучительных поисков.
Скорости коммерческих судов малы с точки зрения изучаемого диапазона относительных скоростей. Баба и Такекума исходили из того, что все основные процессы, которые вносят нелинейные эффекты и влияют на образование поверхностных волн, происходят в тонком слое под свободной поверхностью жидкости. Исходя из этих соображений, они разделили поток вокруг судна на подповерхностный пограничный слой и поток вокруг дублированной модели. Это я идея является замечательной в истории теоретического изучения и расчёта волнового сопротивления судов.
После 13 лет активной работы всех членов мирового сообщества в Токио в 1976 году состоялся новый международный семинар по волновому сопротивлению. Этот семинар имел три основные цели: 1) проследить развитие теории волнового сопротивления по результатам исследований за прошлую декаду и определить будущие направления исследований; 2) рассмотреть тему«как использовать теорию волнового сопротивления для проектирования судов»; 3) предусмотреть благоприятные условия для быстрых обменов неопубликованной информацией, которая полезна для теории волнового сопротивления и проектирования формы корпуса (на этом симпозиуме было высказано пожелание, чтобы японские работы по обсуждаемой проблеме публиковались на английском языке).
 Х. Маруо |
Подготовкой этого семинара в Японии занимался профессор Токийского университета Т. Инуи. Г. Вейнблюм не дожил до этого семинара, но большую организационную помощь оказывали М. Бесшо, Х. Маруо, Х. Кайитани.
На семинаре большое внимание уделялось изучению влияния вязкости, происходящее через ударные и разрушающиеся волны, через пограничный слой и попутный поток. Х. Адачи (Япония) рассмотрел вопрос о деформации носовых волн при прохождении их вдоль корпуса (шелтерный эффект). К. Мори(Япония) предложил метод расчёта поля скоростей в попутном потоке судна.
Несмотря на всю эту огромную работу, пригодный для инженерной практики метод расчёта волнового сопротивления так и не был получен. Оказалось, что горбы и впадины остались на расчётных кривых, полученных даже по теориям второго порядка.
Во вступительной речи Р. Брар сказал, что он не допускал мысли о таком сильном сопротивлении, какое оказывает эта проблема столь мощным усилиям.
1979 год – в опытовом бассейне Токийского университета Инуи и Мията обнаружили волны, которые они назвали FSSW (free surface shock waves) ударными волнами на свободной поверхности. Эти волны дают вклад в виде потери количества движения. Практически они родственны обнаруженной Е. Баба в1969 году вязкостной составляющей сопротивления
 Х. Мията |
При изучении ударных волн была выявлена нелинейная зависимость волнового сопротивления от размерений корпуса судна, от осадки и ширины. Это обстоятельство особенно важно при выборе критериев оптимизации формы корпуса. 80-е годы исследователи Токийского опытового бассейна посвятили двум проблемам: изучению особенностей влияния носового бульба на линейные и нелинейные корабельные волны, и разработке численных методов для расчётов сопротивления движению корпуса судна.
В это время впервые была поставлена и решена задача проектирования корпуса судна, не создающего при движении обычной картины корабельных волн. Несмотря на то, что теоретическому поиску безволновых форм корпуса посвящено много работ, всё-таки отработка таких обводов в опытовом бассейне оказалась более продуктивной. Открытие ударных волн оказалось важным моментом в этой отработке.
Совершенствование вычислительной техники стимулировало разработку численных методов. Начиная с1975 года, проводятся Международные конференции по численным методам в гидродинамике судов (International Conference on Numerical Ship Hydrodynamics). После десятилетий проведения многочисленных расчётов волнового сопротивления судов выяснилось, что для решения волновых задач необходимы вычислительные машины с большим быстродействием и с существенно большей памятью.
Вплоть до 1975 года для расчётов сопротивления воды движению судна использовалась, в основном, теория Мичелла. С появлением более мощных компьютеров численные методы стали главным инструментом.
1976 год – Г.Е. Гэдд использовал замечательную идею: для удовлетворения нелинейных граничных условий на свободной поверхности он использовал такой же способ, как и для моделирования корпуса судна, то есть, с помощью гидродинамических особенностей. Таким образом, Гэдд учёл нелинейные эффекты свободной поверхности и точные условия на поверхности тела. В качестве примера он посчитал волны и волновое сопротивление для судна с тупым носом и с бульбом в носовой оконечности.
1977 год – С. Даусон разработал программу для расчёта волн и волнового сопротивления. Ценность работы Даусона заключается в исследовании и учёте условий рассеяния волн перед и за движущимся судном. Работа Даусона стала базовой почти для всех современных вычислений волнового сопротивления.
Практически во всех опытовых бассейнах мира разработаны комплексы программ для выполнения различных расчётов, в которые обязательно входит определение сопротивления судна. Перечислить и описать все используемые ныне программы невозможно, но есть такие, которые широко известны и используются судостроительными кампаниями. Это программа MICHLET и FLOTSM (Австралия, руководитель Лео Лазаускас), программа KELVIN (Германия, руководитель Генрих Сёдинг), программы RANS и CHAPMAN (Руководитель Л. Ларссон, Чалмерский Университет в Гётеборге); программа CHAPMAN разработана в рамках Европейского проекта CALYPSO, главная работа которого курировалась международной кампанией FLOWTECH, программы ICARE и ISIS (Руководитель Ж. Деламю в Нанте) разработаны для учёта вязкости жидкости в расчётах сопротивления воды движению судна. Программы TUMMAC (Tokyo University Modified Marker-And-Cell) разрабатывались Инуи, Мията и Кайитани в течение20 лет в бассейне Токийского университета одновременно с совершенствованием техники измерений волн. В 1985 автором был депонирован в ВИНИТИ большой обзор около 450 работ по этой проблеме. Сейчас этот список на порядок больше.
История определения сопротивления воды движению судна не закончена. Связано ли это с состоянием компьютерной техники или с недостатком информации о гидродинамических процессах сказать трудно. Сейчас кажется, что решение задачи почти получено. Причём, есть методы расчётов, в которых даже не нужно делить сопротивление на составляющие. Но пока самый мощный на сегодняшний день компьютер считает одну точку на кривой сопротивления один день. Для расчёта всей кривой сопротивления необходимо получить, как минимум, полторы сотни точек. Что покажет такой расчёт, когда он станет возможным, сказать трудно, потому что задача о сопротивлении воды движению судна до сих пор на каждом этапе преподносила и может преподнести новые сюрпризы. В заключение хочется процитировать тезисы Архимеда: «Чем дольше смотришь в воду, тем больше видишь в ней мути» и «имея дело с водой, обратись к опыту».