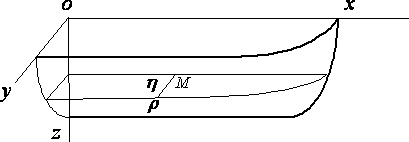
XI. Волновое сопротивление корабля.
Дж. Мичелл. [*] (English)
Объектом настоящего исследования является общее решение проблемы корабельного волнообразования, производимого обводами судна, движущегося с постоянной скоростью в невязкой жидкости, приводящей к последовательному построению кривой волнового сопротивления. Сделано единственное допущение о том, что наклон касательной плоскости в любой точке его поверхности к диаметральной плоскости мал. Это условие не удовлетворяется возле днища на миделе судна у современных судов, но кажется, что это не сильно влияет на вызванные волны или сопротивление, потому что волны возникают скорее возле носа и кормы, где касательная плоскость к поверхности наклонена в направлении движения судна, чем в скругленной средней части корпуса. Пренебрежение вязкостью имеет мало последствий. Завихрение жидкости возле бортов судна, без сомнения, слегка изменяет виртуальную форму корпуса, но это влияет на угол наклона виртуальной касательной плоскости, от которого зависит волновое сопротивление, очень мало. Далее, влияние вязкости на разрушение волн, производимых носом, будет влиять на взаимодействие носовой и кормовой систем волн; но, это волны, длина которых соизмерима с длиной судна, дают основной вклад в волновое сопротивление, влияние вязкости должно быть мало. Отсюда делается заключение, что можно, следуя В. Фруду, разделить сопротивление на сопротивление трения и волновое, и это будет близко к истине.
Обзор экспериментальных работ по этому вопросу, как и краткое изложение теоретических работ Рассела, Рэнкина, двух Фрудов дано в интересной работе Вайта «Manual of Naval Architecture» (1894), часть. xi («Справочник по корабельной архитектуре»). Математика последнего времени по этому вопросу обращена, главным образом, к объяснению интересных наблюдений волновой картины, за исключением статьи сэра Томсона – Кельвина (W. Thomson (Lord Kelvin), Phil. Mag. (1886–7)), в которой критическая скорость в канале, полученная экспериментально задолго до этого Расселом, была описана математически. Можно обратиться к «Гидродинамике» Лэмба (1895) и к «Популярным лекциям» сэра В. Томсона (to Sir W. Thomson's «Popular Lectures on Navigation» (1891), p. 450) для обсуждения волновой картины.
Ни один из этих авторов, однако, не рассмотрел волны, производимые движущимся реальным судном, и настоящая статья предназначена, чтобы выполнить необходимое исследование. Полученная для распределения волн формула довольно сложная, но формула для сопротивления значительно проще, потому что самый сложный член не даёт вклада в волновое сопротивление в идеальной жидкости. Так что будет нетрудно тому, кто захочет сравнить результат с экспериментом. В качестве общего результата для глубокой воды теория приводит к сопротивлению, которое возрастает с увеличением скорости в осциллирующей манере, достигает максимума и затем убывает до нуля, когда скорость растёт до бесконечности. Итак, сопротивление есть осциллирующая функция скорости, что было экспериментально найдено В. Фрудом и его сыном [†] , которому мы обязаны объяснением зависимости интерференции от носовых и кормовых волн. Но безусловное исчезновение сопротивления не ожидается, насколько я знаю. Из общего рассмотрения ясно, что насколько это касается волн, влияние возрастания скорости такое же, как и убывание ускорения силы гравитации, и если гравитация исчезает, то нет перемещения волн, но это не такая теорема, которая может быть получена
Fig. 1
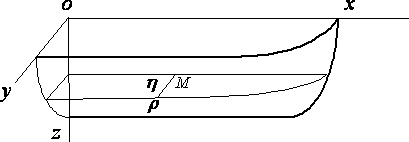
Возьмем вертикальную диаметральную плоскость судна у=0, и поверхность невозмущённой жидкости z=0, ось Ох направлена по направлению движения судна и ось Oz вертикально вниз. Мы можем предположить, что судно находится в покое, а жидкость движется назад с постоянной скоростью v на расстоянии от вызванных волн. Движение предполагается установившимся, и потенциал скорости записывается в виде –vx + f. Поскольку наклон поверхности корпуса к плоскости у=0 везде мал, f мал тоже, и мы можем пренебречь квадратами вызванных скоростей по сравнению с первым порядком f. На поверхности воды пусть высота волы z будет направлена ниже главного уровня ( х,у ). Тогда
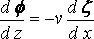 (1)
(1)
является кинематическим условием на свободной поверхности, и
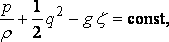
уравнение давления, которое, поскольку
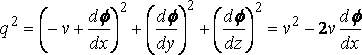 , .... (q.p.)
, .... (q.p.)
дает
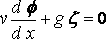
и, следовательно, вместе с (1)
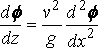 .... (2)
.... (2)
Учитывая симметрию судна относительно диаметральной плоскости у = 0, мы имеем df/dy=0, когда у = 0, за исключением той части судна, где h является полушириной на (x,z),
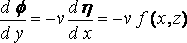 (скажем), ... (3)
(скажем), ... (3)
и это условие принимается на плоскости у=0 вместо поверхности судна, подтверждая то же, что и в уравнении (1). Окончательно, df/dz=0 на дне воды z = h.
Теперь рассмотрим решение для f в той части жидкости, где у положительно, с данными граничными условиями на z = 0, z = h, y = 0.
Типичный член в решении
a cos n ( z–h ) cos ( mx+ a ) cos ( py+ b ),
где: m2+n2+p2=0. Здесь mдолжно быть взято действительным, когда вода простирается от x = –¥ to x = +¥; n и p могут быть либо действительными, либо мнимыми, но если p мнимо [=ip'] последний множитель должен быть взят в форме e–p'y.
Этот член удовлетворяет df/dz=0 на z=h и также удовлетворяет уравнению (2), если:
n tan nh = –v 2m 2/g ..... (4)
Это уравнение имеет бесконечное число действительных корней и один чисто мнимый, который даётся
n' tanh n'h = v 2m 2/g , [n = in'].
Мы видим, что мнимый корень один представляет волновое сопротивление. Так как p всегда мнимое при действительном корне n, то также он мнимый корень, если m>n’.
Условие (3) теперь потребует выражение данной функции f (x, z) в форме
åå amn cos n( z – h ) cos ( mx + a ),
где суммирование по m будет взято в форме интеграла.
Сначала предположим функцию периодической по х так, что
f ( x +l, z ) = f ( x – l, z ),
и положим
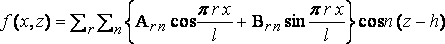 ,
,
где r положительное целое число.
По методу Фурье
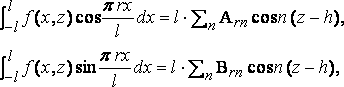
где A0n принимается, как обычно.
Поскольку функции cos n( z – h ) все сопряжённые, то легко показать, что из этого мы получим
и 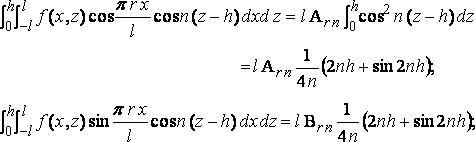
где: A00 должно быть разделено пополам; и коэффициенты членов, данных мнимыми корнями, здесь, как всюду ниже, получены, если положить n=in'; так что

и также для Brn'.
Отсюда следует теорема:
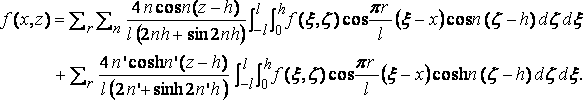
Теперь пусть l станет бесконечным, и положив:
p r / l = m
p / l = dm,
мы получим:
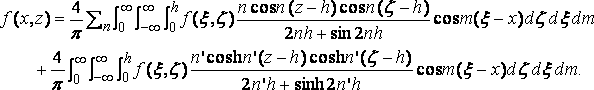
В частности, предполагая глубину жидкости бесконечной, мы имеем тогда:
n h = r p + e ,
h dn = p ,
tan nh = tane,
cos n( z – h )= (–)rcos ( nz– e
),
2n + (sin 2n h ) / h = 2n,
n tan e = – km 2................... [k=v2/g],
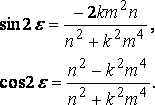
а также:
tanh n'h = 1,
n = k m2,
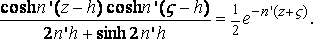
Этот результат получает некоторое подтверждение из того, что было замечено для торпедного катера большой скорости. Было найдено, что полное сопротивление изменяется как некоторая степень скорости, которая сначала равна примерно двум, но потом возрастает до максимума, а затем становится меньше второй. [‡] Очень простое исследование, которое приводится ниже, показывает, что на мелководье, если мы пренебрегаем всеми, за исключением длинных волн, волновое сопротивление меняется, в конечном счёте, как первая степень скорости.
Я могу отметить, что работа, подобная настоящей, даёт теорию подавления осцилляций, благодаря волнообразованию. Это я надеюсь дать в следующей статье.
Подставляя, мы получим выражение
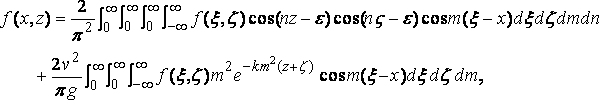
что является теоремой, на которой построена остальная часть настоящей статьи. Доказательство теоремы легко дать априори. Используя величину e , данную выше, мы находим:

Интегрирование последних двух членов по n, viz.
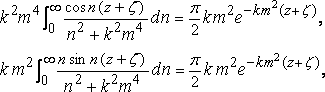
и двойной интеграл становится:
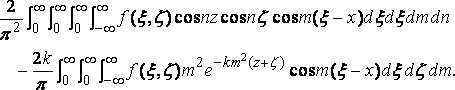
Вышеупомянутый интеграл есть: f( x,z ), и затем исчезает с тройным интегралом в данной формуле.
Рассматривая теперь для простоты воду бесконечной глубины, получаем сразу требуемое решение для f как
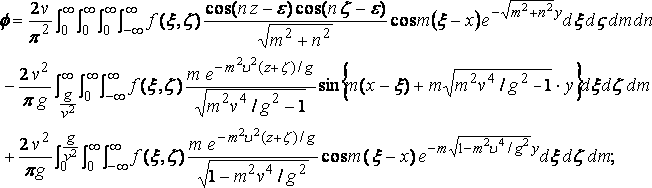 .... (5)
.... (5)
что дает:
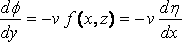 , when y = 0.
, when y = 0.
В этом выражении внимание должно быть обращено на множитель:
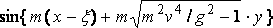
во втором интеграле. Эта форма не требуется для удовлетворения граничных условий, формулированных выше, и очевидно, решение относится к некоторому диапазону, неопределённому для этих условий, так что мы можем наложить любую систему свободных волн, симметричную относительно y = 0, на частное решение, удовлетворяющее их. Вопрос состоит в выборе множителя для того, чтобы сделать элементарные расходящиеся волны следующими за кормой, другими словами, удовлетворить условие, что судно входит в тихую воду.
Оставляя преобразование интегралов с одной стороны, мы переходим к расчёту волнового сопротивления (R).
Пусть dp представляет собой возрастающее давление из-за волнового возмущения. Тогда:
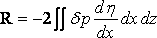 ,
,
двойной интеграл берётся по диаметральной плоскости судна. Теперь, отмеряя от невозмущённой поверхности:
p = p + g r z – ½ r q 2 + ½ r v 2,
и отсюда:
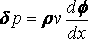 ... (q.p.)
... (q.p.)
та, что:
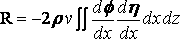 .
.
Подставляя величину df / dx, мы видим, что первый и третий интегралы в выражении для f ничего не добавляют к сопротивлению, потому что:
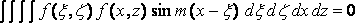 ,
,
из-за нечётного множителя sin ( x - x ), и отсюда:
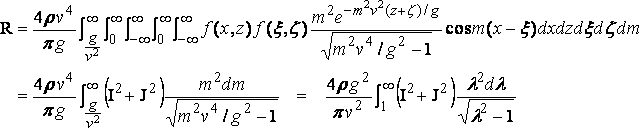 (6)
(6)
где: l = mv2/g, и:
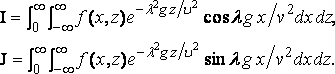
Если судно одинаково в носу и в корме, то I = 0, а начало координат берётся на миделе.
Мы можем теперь доказать, что сопротивление исчезает, когда скорость стремится к бесконечности.
Видим, что:
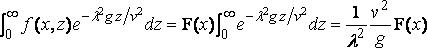 .... (7)
.... (7)
где F( x ) меньше, чем наибольшее значение функции f(x, z) для данной величины х, и отсюда, если мы подставим большое число t, вместо ∞, как верхний предел λ, частью R пренебрежём, потому что её порядок не больше, чем:
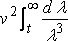 или v 2/t
2,
или v 2/t
2,
и это исчезает, когда v = ∞ если мы возьмём:
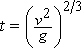 .
.
В части R сохранённая l g/v2 всюду мала, так что мы можем применить круговую функцию и написать:
и 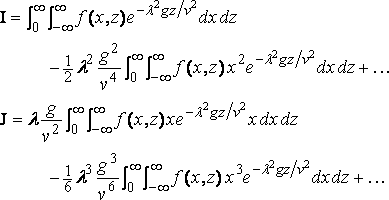
Теперь:
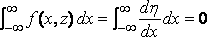 ,
,
судно имеет конечную длину и h = 0 в обеих оконечностях. Тогда, используя формулу (7):
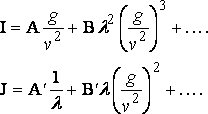
и
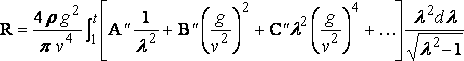
Значимый член имеет порядок:
v–2 log v 2 , v –10/3 , …
и все исчезают, когда v = ∞. Следовательно, сопротивление, в конечном счёте, исчезает. Конечно, этот результат доказан только для очень коротких по сравнению с [§] глубиной воды судов.
Мы теперь приступим к преобразованию интеграла, который даёт сопротивление, с помощью двух элементов поверхности.
Рассмотрим две элементарных площадки s, s' в ( x,z ), ( x',z' ) на борту судна, и пусть θ, θ ' будут наклонами горизонтальных линий в этих элементах к оси x. Сопротивление, благодаря этим двум элементам, равно
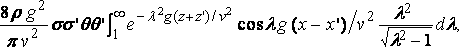
или, скажем:
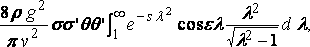
Теперь, приняв на момент z = x + iy, и взяв интеграл
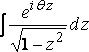
по ограниченной круговой области, где x и y положительны, мы получим:
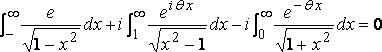 ,
,
и, следовательно [§] , используем
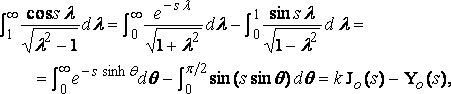 (8)
(8)
где: k = log 2 – g = .11593 … .
Из которого:
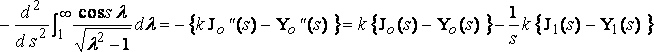 ,
,
поскольку:
J0"(s) + J0'(s)/s + J0(s) = 0
J0'(s) = J1'(s)
[**]и также для Yo(s).
Теперь взяв:
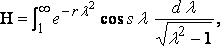
и положив:
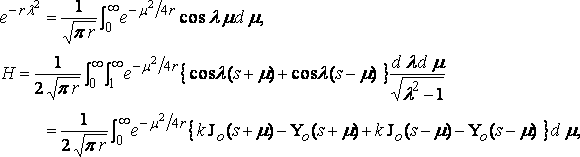 (9)
(9)
из уравнения (8).
H может быть легко посчитано с помощью механического интегратора в случае, когда 4r небольшое, и этот случай является обычным судном. Сложные таблицы J0 и J1 теперь используемые, и таблицы
[**] Y0 и Y1 были посчитаны мистером Б. A. Смитом, который любезно подготовил таблицы kJ0 – Y0 и kJ1 – Y1, и приводятся в этой статье
Теперь мы имеем:
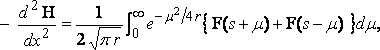
где:
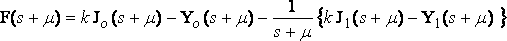 ,
,
и выражение для взаимного воздействия:
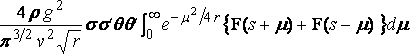 ,
,
где:
r = g ( z + z' ) / v2,
s = g ( x – x' ) / v2.
Элементы на противоположных концах судна s будут в общем большие по сравнению с единицей и с
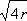 ; и в этом случае мы можем положить:
; и в этом случае мы можем положить:
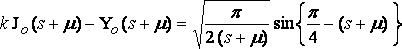 ... q.p.
... q.p.
и также для ( s – m ) и тогда приблизительно:
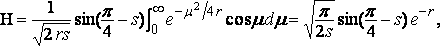
и сопротивление равно:
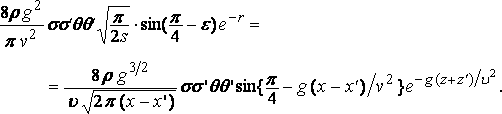
Теперь, если l длина свободной волны, которая перемещается со скоростью судна, и равна:
v2 = g l / 2 p ,
и эта формула может быть написана в виде:
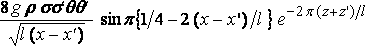 .
.
Это даёт максимум сопротивления, приблизительно, когда
x – x' = ( n+7/8 )·l .......... [n - целое]
и максимум, связанный с
x – x' = ( n+3/8 )·l.
Эта формула соответствует интерференции носовой и кормовой волн, которая была так подробно рассмотрена Р.Е. Фрудом. Когда два элемента находятся на одном и том же вертикальном сечении судна, может быть дана другая форма описания. Положив x – x' = 0, интеграл может быть рассмотрен как:
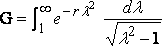 .
.
Положим:
l2 = ½ ( 1+ m),
что дает:
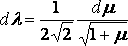 ,
,
и
l2 = ½ (m – 1 );
следовательно:
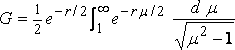
или, если m = cosh f ,
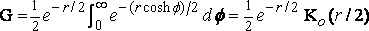 ,
,
где: K0 – Бесселя функция, введённая таким образом Греем и Матье (pp. 67, 90).
Отсюда:
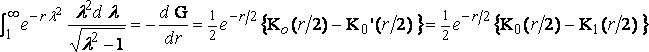 ,
,
поскольку K0' = K1 и соответствующий член в сопротивлении:
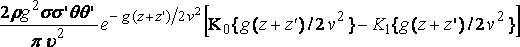
Функции K не были посчитаны, но их общий курс известен. Будет достаточно в настоящий момент следовать Грею и Матье, часть vii.
Как видно из процесса расчёта сопротивления данного судна на любой скорости, мы можем рассмотреть одну простую заданную форму, которая описывает хорошие судовые обводы и легко реализуется. Экспериментальное подтверждение результата не было реализовано, это должно быть оставлено в руках тех, кто имеет необходимый комплект аппаратуры.
Пусть поверхность судна задана в виде:
y = ±c ( 1 + cos ax )( 1 + cos bz ),
между:
x=± p /a,
z = 0 and p /b;
Fig. 2.

так что для положительных значений:
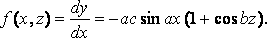
Здесь I = 0, и
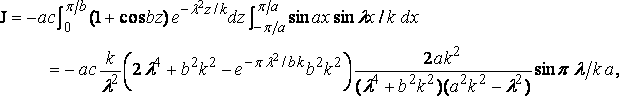
где k = v2/g; и отсюда:
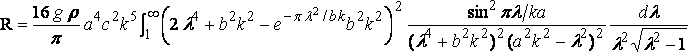
который лучше рассчитывать с помощью механического интегратора.
Предположим, для примера, в квадратных футах:
v = 20 (скорость судна),
2 p /a = 200 (длина судна),
p /b = 20 (осадка ниже ватерлинии),
8c = 32 (наибольшая ширина),
тогда интеграл найден и равен - 620, и сопротивление около: R=940 lbs. wt.
Мне кажется, что-то можно было бы ждать от доступных экспериментальных результатов, но я не знаю никакой формулы, чтобы сравнить это, а эксперимент - это единственное, что может решить, даёт ли теория численное значение. Конечно, метод последовательных приближений может применяться в случае необходимости.
Чтобы проверить случай судна на мелководье, в котором всеми, кроме длинных волн, пренебрегается, мы можем предложить следующее: -
Мы, как прежде, берём установившееся движение и используем такую же систему осей. Уравнение давлений даёт на поверхности:
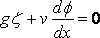 , как и раньше;
, как и раньше;
в то время как уравнение неразрывности для длинных волн даёт:

где h глубина воды, и это даёт:
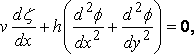 ... (q.p.)
... (q.p.)
Дифференцируя по х и подставляя для f из уравнения давления, мы получаем:
или 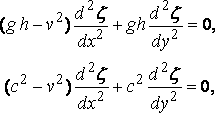
где с скорость свободных длинных волн.
Судно прямостенное и тянется до дна воды, кинематическое уравнение для судна имеет вид:
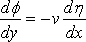 ,
,
которое при дифференцировании по х и использовании уравнения давления даёт
и, конечно же, 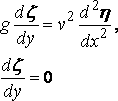
по остальной плоскости y = 0.
Теперь, если v > c, т.е. если скорость судна больше, чем свободных волн, уравнение
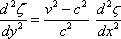
решается в форме:
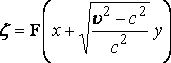 ........
(10)
........
(10)
где граничное условие даёт
 ,
,
или
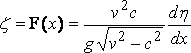 ....... (11)
....... (11)
Форма решения (10) выбрана такого порядка, чтобы расходящиеся волны были за кормой.
Возмущение, следовательно, состоит из двух полос под углом 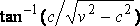 с такой линией движения судна, при которой фронт каждой полосы является горбом над главным уровнем, а его задняя часть является впадиной, которая подобна горбу, если судно имеет одинаковые обводы в носу и в корме.
с такой линией движения судна, при которой фронт каждой полосы является горбом над главным уровнем, а его задняя часть является впадиной, которая подобна горбу, если судно имеет одинаковые обводы в носу и в корме.
Сопротивление (R) даётся в виде:
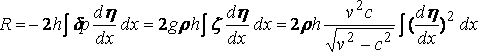 ,
,
так что оно бесконечно, когда скорость судна равна скорости свободных волн, и в конце концов изменяется по скорости.
Если v < c, берутся разные уравнения для потенциальной формы z :
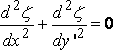 ,
,
при принятом
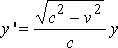 .
.
Теперь решение:
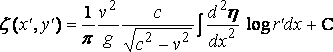 ,
,
где: r' 2 = ( x' – x )2 + y' 2, и здесь нет волнового сопротивления.
Если мы прибавим решения бесконечного числа кораблей, перемещающихся бок о бок на равном расстоянии, мы получим случай судна в середине канала.
В таблице, приведенной здесь, может быть ошибка порядка 1 на последнем месте или, возможно, 2 в величинах x > 3 или 4.
Мельбурнский Университет, 9 августа 1897 г.
Таблица для
k Jo – Y o и k J1 – Y1
Составлена мистером Б.А. Смитом. M.C.E.
| x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) | x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) |
| .00 | ∞ | ∞ | .41 | .9243 | 2.7384 |
| .01 | 4.7200 | 100.0261 | .42 | .8972 | 2.6822 |
| .02 | 4.0274 | 50.0453 | .43 | .8706 | 2.6286 |
| .03 | 3.6215 | 33.3951 | .44 | .8446 | 2.5773 |
| .04 | 3.3331 | 25.0767 | .45 | .8190 | 2.5282 |
| .05 | 3.1091 | 20.0903 | .46 | .7940 | 2.4813 |
| .06 | 2.9258 | 16.7695 | .47 | .7694 | 2.4362 |
| .07 | 2.7705 | 14.4002 | .48 | .7453 | 2.3929 |
| .08 | 2.6359 | 12 6255 | .49 | .7216 | 2.3514 |
| .09 | 2.5168 | 11.2470 | .50 | .6983 | 2.3111 |
| .10 | 2.4099 | 10.1457 | .51 | .6753 | 2 2729 |
| .11 | 2.3133 | 9.2459 | .52 | .6528 | 2.2357 |
| .12 | 2.2245 | 8.4971 | .53 | .6306 | 2.1999 |
| .13 | 2.1428 | 7.8645 | .54 | .6088 | 2.1653 |
| .14 | 2.0670 | 7.3230 | .55 | .5873 | 2.1319 |
| .15 | 1.9961 | 6.8545 | .56 | .5661 | 2.0995 |
| .16 | 1.9297 | 6.4450 | .57 | .5453 | 2 0681 |
| .17 | 1.8671 | 6.0843 | .58 | .5248 | 2.0377 |
| .18 | 1.8079 | 5.7642 | .59 | .5046 | 2 0083 |
| .19 | 1.7517 | 5.4780 | .60 | .4816 | 1.9798 |
| .20 | 1.6982 | 5.2209 | .61 | .4650 | 1.9521 |
| .21 | 1.6472 | 4 9888 | .62 | .4456 | 1.9251 |
| .22 | 1.5983 | 4.7779 | .63 | .4264 | 1.8988 |
| .23 | 1.5515 | 4.5855 | .04 | .4076 | 1.8732 |
| .24 | 1.5066 | 4.4091 | .65 | .3890 | 1.8483 |
| .25 | 1 .4633 | 4.2476 | .66 | .3707 | 1.8241 |
| .26 | 1.4216 | 4 0983 | .67 | .3525 | 1.8005 |
| .27 | 1.3813 | 3.9603 | .68 | .3346 | 1.7775 |
| .28 | 1.3424 | 3.8323 | .69 | .3169 | 1.7550 |
| .29 | 1.3046 | 3.7131 | .70 | .2995 | 1.7329 |
| .30 | 1.2680 | 3.6020 | .71 | .2823 | 1.7114 |
| .31 | 1.2326 | 3.4982 | .72 | .2653 | 1.6904 |
| .32 | 1.1981 | 3.4007 | .73 | .2485 | 1.6699 |
| .33 | 1.1645 | 3.3091 | .74 | .2319 | 1.6496 |
| .34 | 1.1319 | 3.2233 | .75 | .2155 | 1.6299 |
| .35 | 1.1000 | 3.1423 | .76 | .1993 | 1.6105 |
| .36 | 1.0690 | 3.0656 | .77 | .1833 | 1.5914 |
| .37 | 1.0387 | 2.9932 | .78 | .1675 | 1.5728 |
| .38 | 1.0092 | 2.9245 | .79 | .1518 | 1.5544 |
| .39 | .9803 | 2.8593 | .80 | .1363 | 1.5365 |
| .40 | .9519 | 2.7973 | .81 | .1211 | 1.5188 |
Таблица (продолжение).
| x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) | x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) |
| .82 | .1060 | 1.5015 | 4.8 | .4277 | –.3354 |
| .83 | .0910 | 1.4913 | 4.9 | .4588 | –.2817 |
| .84 | .0763 | 1.4674 | 5.0 | .4846 | –.2323 |
| .85 | .0617 | 1.4509 | 5.1 | .5052 | –.1786 |
| .86 | .0473 | 1.4346 | 5.2 | .5203 | –.1214 |
| .87 | .0330 | 1.4185 | 5.3 | .5300 | –.0690 |
| .88 | .0189 | 1.4026 | 5.4 | .5343. | –.0159 |
| .89 | .0050 | 1.3870 | 5.5 | .5332 | +.0373 |
| .90 | –.0088 | 1.3715 | 5,6 | .5269 | .0892 |
| .91 | –.0224 | 1.3563 | 5.7 | .5155 | .1393 |
| .92 | –.0359 | 1.3113 | 5.8 | .4991 | .1873 |
| .93 | –0493 | 1.3261 | 5.9 | .4782 | .2326 |
| .94 | –.0625 | 1.3117 | 6.0 | .4527 | .2749 |
| .95 | –.0756 | 1.2972 | 6.1 | .4232 | .3139 |
| .96 | –.0885 | 1.2829 | 6.2 | .3900 | .3492 |
| .97 | –.1012 | 1.2688 | 6.3 | .3535 | .3805 |
| .98 | –.1138 | 1.2548 | 6.4 | .3140 | .4077 |
| .99 | –.1263 | 1.2108 | 6.5 | .2721 | .4306 |
| 1.0 | –.1386 | 1.2271 | 6.6 | .2281 | .4488 |
| 1.1 | –.2548 | 1.0966 | 6.7 | .1826 | .4625 |
| 1.2 | –.3583 | .9757 | 6.8 | .1358 | .4715 |
| 1.3 | –.4501 | .8616 | 6.9 | .0881 | .4758 |
| 1.4 | –.5304 | .7526 | 7.0 | ..0408 | .4755 |
| 1.5 | –.6008. | .6177 | 7.1 | –.0065 | .4704 |
| 1.6 | –.6604 | .5160 | 7.2 | –.0531 | .4609 |
| 1.7 | –.7101 | .4173 | 7.3 | –.0986 | .4471 |
| 1.8 | –.7500 | .3513 | 7.4 | –.1424 | ..4290 |
| 1.9 | –.7805 | .2583 | 7.5 | –.1842 | .4071 |
| 2.0 | –.8017 | .1682 | 7.6 | –.2237 | .3814 |
| 2.1 | –.8142 | .0812 | 7.7 | –.2604 | .3524 |
| 2.2 | –.8180 | –.0023 | 7.8 | –.2910 | .3203 |
| 2.3 | –.8138 | –.0821 | 7.9 | –.3243 | .2854 |
| 2.4 | –.8017 | –.1580 | 8.0 | –.3510 | .2484 |
| 2.5 | –.7824 | –.2293 | 8.1 | –.3739 | .2093 |
| 2.6 | –.7560 | –.2959 | 8.2 | –.3928 | .1684 |
| 2.7 | –.7234 | –.3576 | 8.3 | –.4076 | .1206 |
| 2.8 | –.6848 | –.4139 | 8.4 | –.4182 | .0840 |
| 2.9 | –.6407 | –.4619 | 8.5 | –.4214 | .0408 |
| 3.0 | –.5920 | –.5100 | 8.6 | –.4264 | –.0020 |
| 3.1 | –.5390 | –.5492 | 8.7 | –.4242 | –.0438 |
| 3.2 | –.4823 | –.5823 | 8.8 | –.4177 | –.0851 |
| 3.3 | –.4227 | –.6092 | 8.9 | –.4071 | –.1251 |
| 3.4 | –.3606 | –.6299 | 9.0 | –.3926 | –.1637 |
| 3.5 | –.2970 | –.6444 | 9.1 | –.3744 | –.2001 |
| 3.6 | –.2320 | –.6525 | 9.2 | –.3527 | –.2343 |
| 3.7 | –.1666 | –.6546 | 9.3 | –.3277 | –.2657 |
| 3.8 | –.1014 | –.6505 | 9.4 | –.2996 | –.2940 |
| 3.9 | –.0368 | –.6406 | 9.5 | –.2688 | –.3194 |
| 4.0 | +.0266 | –.6251 | 9.6 | –.2359 | –.3412 |
| 4.1 | +.0881 | –.6042 | 9.7 | –.2012 | –.3594 |
| 4.2 | .1472 | –.5781 | 9.8 | –.1642 | –.3738 |
| 4.3 | .2035 | –.5472 | 9.9 | –.1261 | –.3845 |
| 4.4 | .2566 | –.5120 | 10.0 | –.0874 | –.3912 |
| 4.5 | .3058 | –.4728 | 10.1 | –.0181 | –.3911 |
| 4.6 | 3510 | –.4300 | 10.2 | –.0087 | –.3923 |
| 4.7 | .3917 | –.3812 | 10.3 | +.0302 |
[*] Communicated by the Author.
[†] 'On the Leading Phenomena of the Wave–Making Resistance of Ships'. Trans.Inst.Naval Architects, 1881
[‡] White, p. 470
[§] See Gray and Mathews, 'Bessel Functions' p.65, and Ex.18, p.230. The formula (8) was given by Weber.
[**] ‘Messenger of Mathematics,’ 1896.
Перевод с английского Ады Шоломовны Готман,
Новосибирская государственная академия водного транспорта.
Philosophical Magazine, 1898, vol. 45, Ser. 5, pp. 106–123.
Phil. Mag, S, .5. Vol . 45 No. 272. Jan. 1898. K