Трехмерная тензорная математика
вычислительных экспериментов в гидромеханике
Вычислительный эксперимент и использование тензорной арифметики
для описания свойств жидкости
©1990-2000, В.Н. Храмушин,
лаб. Вычислительной гидромеханики и морских исследований,
Сахалинский государственный университет,
г. Южно-Сахалинск
 Оглавление
Оглавление
Предпосылки для тензорной арифметики на традиционных векторных формализациях
Вводные определения
Основные предпосылки для построения проекта вычислительного эксперимента
Основные арифметические формализации вычислительных объектов и процессов
Определение идеи, сути и методологии проектирования вычислительного эксперимента
Проектная плоскость для построения алгоритмов вычислительной гидромеханики
О системах отсчета и логических операциях
Определение базовых объектов в пространстве и времени
Определение законов вычислительной гидромеханики
Свойства вычислительных операций и элементарных объектов
Построение вычислительного эксперимента
Вычислительная среда
Простые примеры эффективной численной реализации метода
Заключение
Литература
Предпосылки для тензорной арифметики на традиционных векторных формализациях
Гиперболическое уравнение Гельмгольца о распространении продольных волн в упругой среде допускает каноническое представление математической модели и явную одношаговую постановку вычислительной задачи для построения нестационарных во времени вычислительных экспериментов и тестирования различных, и в том числе гибридных численных схем.
Стандартная математическая модель может иметь классическую форму записи в виде системы дифференциальных уравнений движения гидромеханики. Эта модель довольно легко сводится к одному дифференциальному уравнения движения второго порядка, но в численном решении эти модели не могут быть названы идентичными:
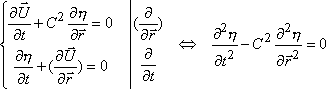 ,
,
где: H = η+D – полный уровень моря, с учетом высоты волны; U=V·H – скоростной поток жидкости учитывает влияние глубины моря; C2=g·H – скорость свободного движения волны здесь выступает в качестве весового коэффициента. В записи уравнений использовано формальное векторное представление пространственной производной для dr, которая соответствует градиенту (grad), а в случае использования простых скобок – как дивергенцию (div), квадратных – ротор (rot). Однако такая формализация математических операций не дает возможности строгой и полной интерпретации физических процессов при построении реальных вычислительных экспериментов в гидромеханике, что обусловлено невозможностью сведения реологических свойств жидкости к одной - бесконечно малой точке.
Аналогичную по форме численную модель можно построить прямым рассмотрением сил на границах малого деформируемого контрольного объема (метод конечного объема), когда дифференциалы изначально трактуются в виде конечных разностей.
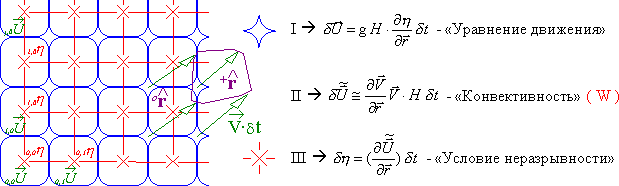
Традиционный вычислительный эксперимент с данной математической моделью (распространение длинных волн в океане) обычно ограничивается двумя этапами, которые выше отмечены римскими цифрами I и III, но даже в такой упрощенной постановке моделирование показывает практические результаты не доступные для теоретического анализа, но вполне согласующиеся с наблюдениями в природе. Включение в вычислительную модель этапа II, который, по сути, является интерполяционным аналогом экстраполяционных условий на свободных границах, обычно сопряжен с серьезными теоретическими сложностями, - которых удается избежать при использовании конечно-разностных моделей новой тензорной математики.
Вводные определения
Вычислительные эксперименты в механике сплошных сред опираются на собственный математический аппарат конечных разностей, в основе которого лежат аппроксимации непрерывных функций ограниченным количеством опорных величин, распределенных в дискретных ячейках памяти цифровой ЭВМ. Определенные таким образом непрерывные в пространстве и времени процессы, не вполне соответствуют предположениям классического дифференциального анализа, законы которого справедливы для предельно близких интерполирующих точек, количество которых на ограниченном отрезке должно стремиться к бесконечности. По сути же, классические численные методы могли бы быть эффективными при их использовании на аналоговых моделирующих или вычислительных устройствах, но, к сожалению, здесь имеется множество чисто фундаментальных математических проблем, в первую очередь обусловленных недостаточностью аппарата дифференциального исчисления для точного описания и прямой интерпретации физических свойств многомерных векторных полей.
Практически не существует прикладных вычислительных экспериментов в гидромеханике, в которых математическая модель и ее численная реализация обеспечивали бы безусловное и с заданной точностью решение задачи в произвольной расчетной области и при любых режимах течения жидкости. Но для того, чтобы обеспечить надежный контроль качества численного решения и своевременное применение усложненных или гибридных алгоритмов, при проектировании вычислительных экспериментов очень важно обеспечить возможность физической интерпретации всех, и том числе тривиальных вычислительных операций ЭВМ. Тогда:
1) Элементарные объекты гидромеханики должны определяться только в размерной форме;
2) Вычислительные операции должны быть определены в строгой взаимосвязи физических свойств жидкости и законов механики, которые должны применяться в условиях автоматического преобразования координатных величин и пересчета физических размерностей;
3) Свойства вычислительных операций и элементарных числовых объектов определяются как в единой – абсолютной системе координат, так и в локальных - дуальных базисах, связанных с конкретными частицами жидкости.
 Формально векторный Закон Ньютона может быть построен с помощью тензорной операции умножения, где внешняя сила
Формально векторный Закон Ньютона может быть построен с помощью тензорной операции умножения, где внешняя сила 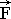 задается в абсолютной системе координат, а реакция
задается в абсолютной системе координат, а реакция 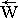 – уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы
– уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы  будет исполнять роль не только аккумулятора энергии поступательного движения, но также учтет инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
будет исполнять роль не только аккумулятора энергии поступательного движения, но также учтет инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
Вычислительные модели гидромеханики в каноническом представлении удобно формализовать с помощью линейных аппроксимирующих функций, точные физические величины которых определяются на разреженных узлах конечно-разностной сетки, охватывающей ограниченную область течения жидкости. Аналитические методы Исаака Ньютона позволяли в разностной форме выполнить постановку и прямое численное решение многих одномерных интерполяционно-динамических задач. Однако, несмотря на эффективность и универсальность ньютоновских численных решений, это направление математических исследований затруднялось необходимостью использования сложных численно-логических схем (в современной терминологии – алгоритмов). Современная компьютерная логика позволяет обобщить разностные методы решения задач гидромеханики путем применения функционального программирования для формализации основных числовых объектов и вычислительных операций. Для явного контроля физических процессов законы движения жидкости изначально представляются в жестких логических операциях трехмерной тензорной арифметики, оперирующих конкретными параметрами течения в размерном виде.
Трехмерная тензорная математика формализует описание явлений гидромеханики именно для того случая, когда непрерывные функции определяются с помощью ограниченного количества не очень близко расположенных аппроксимирующих пространственно-временных точек. Важным преимуществом такой постановки вычислительного эксперимента в гидромеханике явилась возможность более глубокого понимания многих законов и явлений, сопровождающих течение реальных жидкостей. Разработка же формализованных правил для компьютерной реализации вычислительных экспериментов в тензорной постановке, сама по себе составила интереснейшую задачу, которая позволила вновь коснуться как математических основ гидромеханики, так и фундаментальных понятий физики в целом. Оказалось, что тензорная арифметика и логика вычислительных операций позволяют проследить физические аналогии всех вычислительных операций и построить комплекс алгоритмических объектов наиболее полно определяющих суть и форму вычислительных процессов при моделировании физических явлений и механики жидкости.
Основные предпосылки для построения проекта вычислительного эксперимента
При построении новых математических операций и вычислительных объектов не будет использовано никаких новых гипотез об относительности систем отсчета и неопределенности внутренних свойств жидкости. Главная или общая система координат является всегда ортогональной и ортонормированной. Отсчеты времени всегда задаются скалярными величинами и используются только для фиксации во времени всего вычислительного процесса, иногда состояния его отдельных подобластей или жидких частиц. Однако исходное пространство и время всегда наделяются свойствами идеальности, то есть, глобальны и абсолютны по проявлениям, непрерывны, линейны и недеформируемы.
Пространство не терпит пустоты и при необходимости заполняется Эфиром со свойствами вязкой и сжимаемой жидкости. С каждой частицей жидкости связывается локальная система координат с теми же внутренними свойствами, что и абсолютная система отсчета. Локальная и абсолютная системы координат строго связаны между собой как по физическим свойствам и размерностям наполняющих их жидкостей, а также с помощью строгих правил выполнения тензорных математических операций и преобразований.
Традиционная физическая интерпретация, так же как и численное решение задач гидромеханики, опирается на два взаимосвязанных и существенно отличающихся по форме геометрических представления о течении жидкости, - это известные дифференциальные формализации течений по Эйлеру – на фиксированной сетке и изменяющихся значениях гидродинамических полей, и по Лагранжу – с фиксацией законов сохранения внутри каждой из движущихся частиц жидкости.
Опыт реализации вычислительных экспериментов показывает, что для сложных расчетных областей невозможно применение дифференцирующих разностей более чем первого порядка. Задачи же механики опираются на уравнения движения второго порядка, которые в случае задач аэрогидромеханики довольно уверенно моделируются с использованием разделения решения на подэтапы, где последовательное использование интерполирующих функций первого порядка сначала опирается на неподвижные узлы сетки, затем ведется расчет в локальных координатах подвижных частиц жидкости. Такой подход к решению соответствует классическому разложению дифференциальных уравнений гидромеханики по физическим параметрам, который выполняется в Лагранже-Эйлеровых схемах, методе «Крупных частиц» или «Конечного объема». Суть разложения по физическим параметрам, при таком подходе, выражается в двойном последовательном дифференцировании первого порядка, что, в свою очередь, разделяет каждый временной цикл вычислительного эксперимента на три этапа:
1 этап – вычисляются кинематические параметры для динамических центров крупных частиц жидкости, для чего используются текущие исходные данные в неподвижных узлах конечноразностной расчетной сетки, которая обычно обладает свойствами неподвижных Эйлеровых координат;
2 этап – Лагранжевы или крупные деформируемые частицы жидкости участвуют в свободном движении, перераспределяя внутренние свойства исходных Эйлеровых ячеек по смежному с ними пространству;
3 этап – согласуются законы сохранения массы и энергии, что достигается поляризацией или деформацией сдвинутых частиц жидкости, с последующей переинтерполяцией характеристик течения в исходные узлы неподвижной Эйлеровой расчетной сетки.
Для построения вычислительного эксперимента по указанной схеме каждая из частиц жидкости должна вести себя как своеобразный энергоемкий объект, подчиняющийся законам сохранения энергии в пределах геометрического объема этой частицы, часть которой тратится на простую передачу движения смежным частицам, а часть на консервацию энергии движения внутри элементарной частицы жидкости. Это может проявляться как безвозвратная потеря энергии движения на трение при деформации жидкой частицы, а также как аккумулируемая энергия, в том числе обусловленная изменением интенсивности замкнутых течений внутри такой элементарной частицы жидкости (образование/затухание внутренних диполей).
Основные арифметические формализации вычислительных объектов и процессов
Физические размерности являются естественным и наилучшим предикатом вычислительной формализации гидродинамических объектов. Такие же предикаты необходимы для фиксации типа системы отсчета и пространственной привязки к конкретной конечномерной частице жидкости. В комплексе вся система признаков-предикатов необходима для автоматизированного распознавания и применения базовых функций трансформации элементарных объектов к требуемому расчетно-каноническому виду, с последующим применением конкретных гидромеханических моделей, и обратному преобразованию результатов к требуемой системе отсчета. Элементарные объекты определяются в одной из трех разностных форм:
1) Скаляр – числовая величина, не зависящая от системы отсчета, являющаяся либо инвариантом пространственно-временных преобразований, либо эмпирической величиной, формализующей реологические свойства жидкости (в обобщенном случае это одно и то же). Может использоваться только в операциях произведения, с любыми объектами;
2) Вектор – задает пространственно ориентированное внешнее воздействие или реакцию на него со стороны элементарной жидкой частицы. Векторные величины всегда связаны с конкретным пространственным базисом. Допускаются операции сложения для величин, измеренных в одной и той же системе отсчета и с одинаковыми физическими размерностями, а также операции умножения векторов на тензоры, в результате которых происходит замена или уточнение опорного базиса;
3) Тензор II ранга – является производной величиной, характеризующей локальные свойства геометрических преобразований, или фиксирующей динамическое состояние элементарной жидкой частицы. Тензорные объекты можно интерпретировать в качестве пространственных базисов, которые хранят геометрию деформирующейся жидкой частицы, и задают их локальную (внутреннюю) кинематику и конвективные свойства. Тензоры всегда участвуют в анализе динамических свойств и режимов течения реальной жидкости. Любые преобразования тензорных величин выполняются только в соответствии с логикой представления физических процессов и законов гидромеханики. Тензорные операции могут определяться чисто лингвистическими правилами языков программирования (их внутренней семантикой), что позволяет в процессе вычислительных экспериментов задействовать гибридные математические модели или параллельно использовать существенно различающиеся гидродинамические модели течения.
По физической сути тензор II ранга наиболее близко соответствует понятию аффинора, введенного в использование Людвигом Прандтлем в книге «Гидро- и аэромеханика» [1932], где тензором называлась только симметричная часть аффинора, а выделяемая антисимметричная часть аффинора определялась в качестве вектора вращения.
К настоящему времени утихли дискуссии о методах вычислительной гидромеханики, на фоне которых наиболее ярко проявилась публикация в 1982 году книги О.М. Белоцерковского и Ю.М. Давыдова «Метод крупных частиц в газовой динамике», содержащей наиболее выразительное и точное описание вычислительных экспериментов в гидромеханике с использованием Лагранже-Эйлеровых подходов. В этой же книге выполнен анализ и обоснование физической сути дифференциальных приближений, которые используются в вычислительных моделях гидромеханики при замене классических дифференциальных уравнений в частных производных их конечно-разностными аппроксимациями.
В 1990 году вышел двухтомник Андерсона Д, Таннехилла Дж и Плетчера Р. «Вычислительная гидромеханика и теплообмен», в которой были обобщены и систематизированы многие вычислительные модели. В этой книге появился примиряющий термин: «Метод конечного объема», который определяет метод достаточно близкий по смыслу тензорному построению вычислительных экспериментов, но, к сожалению, это справедливо только в отношении к постановочной части гидромеханической задачи «метода конечного объема».
Поэтому стоит вернуться к основным идеям и численным реализациям метода «Крупных частиц жидкости», тем более, что полученные в данном исследовании тензорные формализации уравнений гидроаэромеханики впервые отрабатывались и проверялись с помощью свертывания к тензорной форме больших систем разностных уравнений метода Крупных частиц, приведенных в книге О.М. Белоцерковского и Ю.М. Давыдова [1982].
Тензорные операции с элементарными объектами гидромеханики, их свойства и правила арифметических преобразований наиболее близко соответствуют принятым в книге Дж. Астарита и Дж. Маруччи «Основы механики неньютоновских жидкостей» [1978], от нотации и смыслового содержания которых здесь не делается существенных отклонений.
Определение идеи, сути и методологии проектирования вычислительного эксперимента
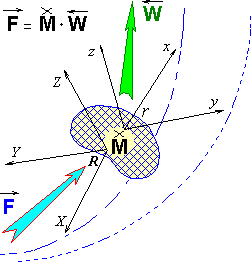
Воспользуемся обобщенным базисом троичной логики для формального представления объекта исследований, целью которого является изучение возможности комплексного решения задачи о проведении вычислительного эксперимента в гидромеханике, где математический аппарат должен быть строго согласован с алгоритмическим описанием физических процессов, и обеспечивать эффективное (или автоматизированное) проектирование численных схем и алгоритмов для решения как прямых, так и обратных задач гидромеханики.
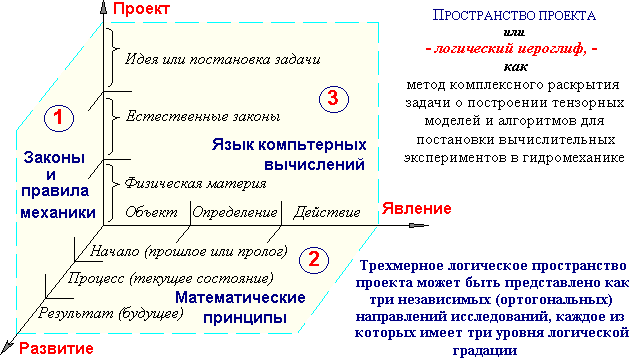
На рисунке выше представлено трехмерное логическое пространство, базисные плоскости которого образуют главные направления настоящего исследования. Секторы, образованные градациями по направлениям, определяют строение, название и смысловое содержание каждого из параграфов. Такой троичный базис позволяет согласовать противоречия при использовании встречных подходов к проектированию сложных логических систем. С этой целью противоречивые требования соотносятся между собой с позиций третьего - ортогонального и независимого от двух первых методологических подходов. С позиций такого третьего направления, названного к примеру: «Проект», могут быть согласованы (ортогонализованы) противоречия различных логических подходов, которые при корректном логическом проектировании обязательно должны дополнять друг друга. В нашем случае таким третьим направлением может выступить описание процессов вдоль оси «Явление», используемого по правилам «существительного» в предложении естественного языка, и ось-определение «Развитие» соотносимое с понятием «процесса» или «действия», – подобно глаголу. Тогда плоскость оси «Проект» будет выступать в роли логического поля для согласования обоих подходов к численному решению задач гидромеханики.
К логическому базису можно применять логические преобразования, аналогичные стандартным операциям тензорного анализа с учетом физических размерностей и соглашений об абсолютной и локальной системе отсчета. Полученные таким образом метафизические правила преобразования логических тензоров (матриц) могут быть использованы для разделения алгоритмов компьютерных вычислений на функциональные и декларативные методы программирования, в соответствии с требованиями по интерпретации исходных данных (существительных) и математических операций (глаголов).
По условиям проектирования «снизу-вверх» - направление от плоскости «Проект-Развитие», может быть изучена систематизация законов гидромеханики и тензорного анализа с позиций логики вычислительных операций. Это необходимо для формального определения гидродинамических величин и объектов, базисов и пространства их существования и областей для определения числовых величин, которые должны быть связаны жесткими правилами тензорных арифметических операций и вычислительных алгоритмов для автоматических преобразований при изменении систем отсчета. Реальные вычислительные модели и их свойства могут быть изучены в соответствии с другим ортогональным (независимым) направлением исследований, которое будет привязано к оси матрицы: «Развитие-Явление», и на котором строится обоснование достаточности аргументов (исходных условий) при теоретическом обосновании нового математического аппарата вычислительной гидромеханики. Ось «Явление-Проект» может быть ассоциирована с изучением специализированного языка программирования для решения задач вычислительной гидромеханики, который должен быть спроектирован и реализован для наиболее эффективного использования законов и математических принципов формализованных в двух других ортогональных плоскостях (независимых направлениях исследований), в рамках единого троичного логического базиса (настоящего исследования).
«Язык компьютерных вычислений» находится в стадии перспективного проектирования, являясь источником и целью излагаемой здесь «Трехмерной тензорной математики вычислительных экспериментов в гидромеханике», поэтому данный вопрос должен включать три подраздела, образующими диагональную или каноническую матрицу исходного проекта. Это означает, что логическая матрица для исследования проекта тензорного языка программирования, должна быть предварительно подготовлена к упрощенным процедурам для «прямого хода» проекта, который должен методично корректироваться за счет «обратного решения», означающего дальнейшую детализацию и - формализацию условий, необходимых для построения новых методов практической реализации вычислительных экспериментов в гидромеханике.
Проектная плоскость для построения алгоритмов вычислительной гидромеханики
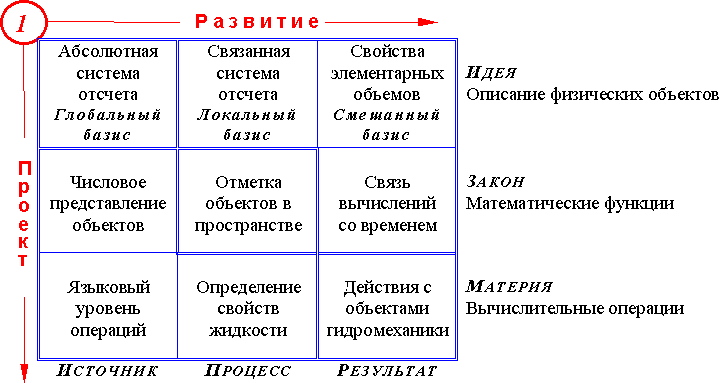
Структура троичной матрицы, определяющей взаимосвязь элементарных объектов вычислительной гидромеханики, применяемых к ним математических операций и логики пространственно-временных преобразований.
В плоскости «Проект-Развитие» выполняется описание вычислительного эксперимента, как физического «Явления» моделируемого с помощью логических объектов и операций ЭВМ.
Формально, методология «построения тензорной математики для проектирования вычислительных экспериментов в гидромеханике» может быть представлена по правилу исследовательского проектирования «сверху-вниз», которое возможно при условии, когда основные математические инструменты и вычислительные алгоритмы уже известны и опробованы на практике. Учитывая, что в этом случае каждый элемент троичной матрицы может быть предметом самостоятельного исследования и законченного повествования, изложение материала может быть максимально кратким для первых параграфов (верхних строк матрицы), и расширяться по мере приближения к практическим вопросам нижней строки троичной матрицы.
Главным объектом исследования является конечный объем подвижной и деформируемой сплошной среды (крупная частица или конечный объем жидкости), заключенной в геометрическое пространство, ограниченное симплексом из смежных узловых точек. Такие частицы жидкости образуют элементарные или базисные объекты вычислительной гидромеханики, с которыми связываются реологические, инерционные и энергетические свойства локальных течений. Внутри элементарной частицы, в строгой форме определяются законы независимого существования и взаимодействия между смежными объектами сплошной среды. Такой симплекс из смежных пространственных точек математически определяется в форме тензора II ранга, которые задает локальный базис для фиксации внутренних свойств жидкой частицы, которые могут однозначно переопределяться в абсолютной или глобальной системе отсчета, а также соотноситься с помощью линейных/обратных зависимостей с аналогичными смежными частицами жидкости, участвующих в неразрывном течении жидкости.
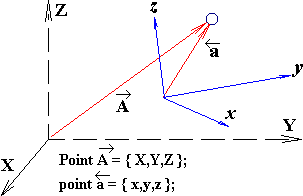 Геометрически частица жидкости {
Геометрически частица жидкости { /
/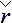 } может быть представлена в виде
параллелепипеда / эллипсоида, внутреннее состояние которого формализуются линейными / обратными распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных / локальных базисов (трехмерных тензоров II ранга), задающих линейное/обратное распределение внутренних свойств течения между жидкими частицами, которые однозначно связаны интерполяционными (без экстраполяции) зависимостями с исходными узлами расчетной области.
} может быть представлена в виде
параллелепипеда / эллипсоида, внутреннее состояние которого формализуются линейными / обратными распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных / локальных базисов (трехмерных тензоров II ранга), задающих линейное/обратное распределение внутренних свойств течения между жидкими частицами, которые однозначно связаны интерполяционными (без экстраполяции) зависимостями с исходными узлами расчетной области.
О системах отсчета и логических операциях
Все математические построения выполняются исключительно в размерной форме, где физические размерности и признаки принадлежности к пространственной системе отсчета, являются главными предикатами логических алгоритмов, которые, в идеальном случае, обеспечивают автоматическое построение вычислительных экспериментов гидромеханики.
Главная или общая система координат {X,Y,Z} является всегда ортогональной и ортонормированной. Отсчеты времени задаются скалярными величинами, фиксирующими состояние либо всего вычислительного процесса, либо его отдельных подобластей. Такое исходное пространство и время всегда наделяются свойствами идеальности, то есть, они глобальны и абсолютны по своим физическим проявлениям, а также непрерывны, линейны и недеформируемы.
В постановке задачи не используется понятия пустоты. Пространство заполняется реальной жидкостью или эфиром со свойствами вязкой и сжимаемой среды, являющихся носителем внутренней энергии, проявляющейся как инерция. С каждой пространственно ограниченной частицей жидкости связывается собственная или внутренняя
локальная система координат {x,y,z}, с теми же физико-механическими свойствами что и абсолютная система отсчета.
Абсолютная и локальные системы отсчета строго связаны между собой физическими свойствами (размерностями) наполняющих их жидкостей, а формализация этих свойств однозначно определяет логические правила применения законов механики, а также весь комплекс взаимных преобразований расчетных величин, которые выполняются в рамках компьютерного аппарата тензорной арифметики.
Сформулированные условия построения вычислительного эксперимента в гидромеханике обеспечивают независимость (реентерабельность) применения тензорных операций, как на момент применения законов механики для образования нестационарности течения, так и на последующих этапах интерполяционного согласования свойств жидкости в разных системах отсчета с применением законов сохранения, граничных и начальных (здесь это – внешних и внутренних) воздействий. Такая независимость и унифицированность компьютерных операций может быть использована как для переноса базовых вычислительных алгоритмов на аппаратный уровень ЭВМ, так и с целью распараллеливания расчетных процессов при проведении вычислительного эксперимента.
Определение базовых объектов в пространстве и времени
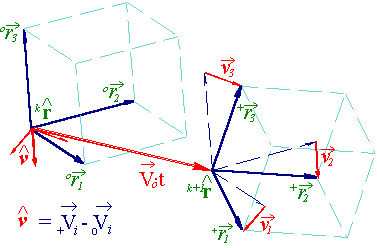
Пространственное описание крупных частиц жидкости выполняется в расширенной тензорной нотации в двух взаимосвязанных системах координат. 1) – абсолютной
- или неподвижной (Эйлеровой) сетке узловых величин, которая является единой и глобальной системой отсчета для всего вычислительного эксперимента. Вычислительные объекты, связанные с абсолютной системой отсчета, обозначаются прописными буквами. 2) – локальной - или естественным базисом конкретной крупной частицы жидкости, участвующей в свободном (Лагранжевом) движении по собственной траектории, и в которой определяются внутренние свойства конкретной крупной частицы жидкости. Вычислительные объекты, определенные в таком естественном базисе обозначаются строчными буквами.
Прописными (заглавными) буквами всегда будут обозначаться величины, измеренные в абсолютных системах отсчета (Rk. – вектор координат для точки в пространстве).
Строчными буквами обозначатся величины, измеренные внутри локальных (подвижных) базисов (rk – вектор локальных координат точки, определенной в связанной системе отсчета внутри конкретной частицы жидкости);
Левые верхние индексы будут отмечать текущие отсчеты во времени, к которым относятся вычислительные объекты или процессы.
Левые нижние индексы будут отмечать номера или индексы пространственных ячеек сеточной области, которые можно трактовать как неподвижную Эйлерову или абсолютную систему координат. Исходное местоположение крупной частицы жидкости размечаемую левыми нижними индексами с прописными буквами { J,K }, или как пространственные метки подвижных частиц жидкости, которые будут отмечаться строчными индексами { j,k }.
Все правые индексы являются тензорными идентификаторами и обозначают принадлежность к системе отсчета. Нижние индексы привязывают объект к абсолютной системе координат, верхние – соответственно, к локальному базису. Векторные стрелки могут заменять индексы, при этом стрелка вправо → отмечает принадлежность к абсолютной системе отсчета (нижний индекс), влево ← к локальной (верхний индекс). Тензорные величины отмечаются двойными индексами или уголками: Ù - абсолютная; Ú - локальная; >,< и × смешанные системы отсчета.
Отсчеты времени всегда абсолютны и скалярны. Время T, отмеченное прописной буквой, исчисляется от момента начала вычислительного эксперимента; стр – оочной tтмечается интервал времени, используемый в качестве расчетного шага: t = +T–oT.
Скалярные величины иногда удобно использовать в качестве индексов для привязки вычислительных объектов (крупных частиц жидкости) в пространстве – левый нижний индекс, и во времени – левый верхний индекс. Если левые индексы отсутствуют – это означает, что в вычислительной операции определяется действие применимое к любой частице жидкости.
Индекс Т, отмеченный прописной буквой, означает абсолютный отсчет времени, а индекс t – строчной буквой, будет означать разность времен между смежными вычислительными шагами (процессами) во времени, т.е. временные разности. Если время в вычислительном эксперименте связано с тактами
k, то: +T = k+1T=0T+(k+1)·t, где левый верхний индекс указывает на текущий расчетный такт во времени. t – расчетный интервал времени;
ΩtR – координаты узловой точки, где: Ω – левый нижний индекс определяет местоположение узла в расчетной области; T – момент времени от начала проведения вычислительного эксперимента; → - стрелочка вправо указывает на абсолютную систему координат.
+tR– ссылка на смежную точку, относительно ΩtR, смещением в пространстве в сторону (+) с учетом смещения подвижного и деформирующегося ограниченного объема жидкости Ω (крупной частицы) за время t. ← - стрелка влево показывает, что «длинный» вектор абсолютных координат 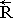 измеряется в локальной системе отсчета, связанной с текущим состоянием и местоположением крупной частицы жидкости.
измеряется в локальной системе отсчета, связанной с текущим состоянием и местоположением крупной частицы жидкости.
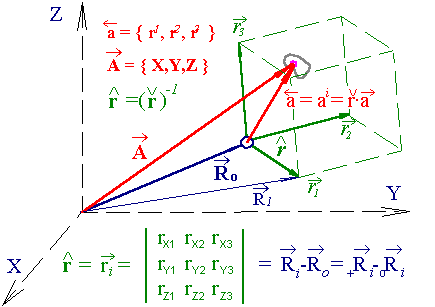
 = rij =
= rij = 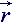 i =
+
i =
+ i - Ω
i - Ω i – тензорное определение формы крупной частицы жидкости в абсолютной системе координат. Геометрически такой тензор подобен базисному параллелепипеду, определяется на векторах
i – тензорное определение формы крупной частицы жидкости в абсолютной системе координат. Геометрически такой тензор подобен базисному параллелепипеду, определяется на векторах 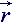 i
, ориентированных на смежные точки пространственного симплекса.
i
, ориентированных на смежные точки пространственного симплекса.
По аналогии: 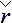 =
=  -1 – обращение тензора переводит его к дуальному базису;
-1 – обращение тензора переводит его к дуальному базису;
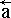 =
= 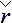 ·
· 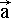 – вектор переходит из абсолютной в локальную систему координат. Для перестройки вектора из локальной системы отсчета к абсолютной – необходимо добавить координаты базовой точки крупной частицы жидкости:
– вектор переходит из абсолютной в локальную систему координат. Для перестройки вектора из локальной системы отсчета к абсолютной – необходимо добавить координаты базовой точки крупной частицы жидкости: 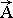 =
=
 +
+  ·
·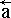 .
.
Аналогично, в виде конечных разностей вводится динамическое понятие приращения скорости: Δ = +
= + - o
- o . Реологические свойства жидкости, которые в традиционной гидромеханике задаются скалярами, в вычислительном эксперименте всегда проявляются в виде тензорных описателей внутренних свойств, для которых уже в ходе вычислений ведется контроль сохранения требуемых физических свойств, параллельно с выполнением контроля корректности критериев существования самого численного решения.
. Реологические свойства жидкости, которые в традиционной гидромеханике задаются скалярами, в вычислительном эксперименте всегда проявляются в виде тензорных описателей внутренних свойств, для которых уже в ходе вычислений ведется контроль сохранения требуемых физических свойств, параллельно с выполнением контроля корректности критериев существования самого численного решения.
Определение законов вычислительной гидромеханики
Пусть в качестве исходных данных для построения вычислительного эксперимента в гидромеханике будут определены следующие размерные поля в абсолютной (глобальной) системе координат:
{ } [м] – поле координат узловых точек;
} [м] – поле координат узловых точек;
( ) [м/с] – поле скорости;
) [м/с] – поле скорости;
{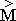 } [кг] – тензорное поле внутренних свойств частицы.
} [кг] – тензорное поле внутренних свойств частицы.
В определенной таким образом сеточной области вводятся локальные вычислительные объекты - как элементарные крупные частицы жидкости, в которых определяются физические параметры течения жидкости, определенные в той же абсолютной системе координат:
 [м3] – тензор формы крупной частицы;
[м3] – тензор формы крупной частицы;
 [м3/c] – тензор локальных (конвективных) скоростей;
[м3/c] – тензор локальных (конвективных) скоростей;
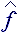 [Н·м2] – тензор напряжений.
[Н·м2] – тензор напряжений.
Основные законы механики для деформируемой жидкой частицы в тензорном виде получаются не сложнее обычных арифметических операций, которые удивительно похожи по форме и по сути как для внешних сил, так и для внутренних деформаций. Это позволяет на всех этапах численного решения оперировать довольно простыми аналитическими зависимостями, которые, к тому же, учитывают эффекты аккумуляции и последующего излучения механической энергии, полученной в результате внешних взаимодействий между смежными расчетными ячейками. Такая внутренняя энергия частиц может достигать больших величин, если в тензоре конвективных скоростей будут наблюдаться вихревые или дипольные эффекты, которые в первом приближений и задают изменение направления реакции на внешние силы, а также изменение величины инерции частицы жидкости, соответственно.
1. Векторный закон Ньютона для деформируемой частицы: 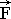 =
=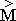 ·
·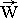 ; (1)
; (1)
2. Тензор вязких напряжений для Ньютоновой жидкости:  Н =
Н = 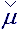 ·
· =
= 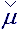 ·
· ·
·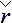 ; (2)
; (2)
3. Тензор упругих напряжений для твердого тела Гука:  Г =
Г = 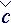 ·(1+
·(1+ ·t) =
·t) =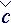 ·(
·( +
+ ·t)·
·t)·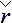 . (3)
. (3)
Тензор вязких напряжений получается выделением кососимметричной части из матрицы локальных скоростей для тензора  , антисимметричная часть которой задает вращение частиц:
, антисимметричная часть которой задает вращение частиц:  Н =
Н = 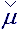 ·
· H
=
H
= 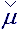 ·(
·(  *-
*-  * T)/2. Оставшийся симметричный тензор связывается с упругой деформацией:
* T)/2. Оставшийся симметричный тензор связывается с упругой деформацией:  Г =
Г = 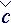 ·
· Г =
Г =
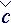 ·(
·(  *-
*-  * T)·t/2. Соответственно полный тензор внутренних напряжений:
* T)·t/2. Соответственно полный тензор внутренних напряжений:  = (
= (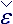 ·
· 0+
0+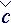 ·
· Г)·t/2 +
Г)·t/2 + 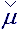 ·
· H.
H.
 Здесь снова строчными буквами обозначены вычислительные объекты, заданные в локальных координатах конкретных частиц жидкости, а прописными – формализованные функции, определенные в абсолютной системе координат. Обозначения:
Здесь снова строчными буквами обозначены вычислительные объекты, заданные в локальных координатах конкретных частиц жидкости, а прописными – формализованные функции, определенные в абсолютной системе координат. Обозначения:  = vij
=
= vij
= 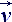 i = +
i = + i - Ω
i - Ω i
– тензор локальных скоростей;
i
– тензор локальных скоростей; 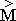 = M i j =
= M i j =  ·
· = rij·ρ jk – тензор инерции (масса) в проекции на абсолютную систему отсчета;
= rij·ρ jk – тензор инерции (масса) в проекции на абсолютную систему отсчета;  – тензор деформации (плотность) или аккумуляции внутренней энергии;
– тензор деформации (плотность) или аккумуляции внутренней энергии; 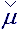 ,
, 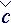 – тензоры динамической вязкости и жесткости жидкости.
– тензоры динамической вязкости и жесткости жидкости.С тензором плотности
 связывается предыстория деформации элементарных расчетных объектов, что позволяет на лагранжевом этапе вычислительного эксперимента считать крупные частицы жидкости как участвующие в свободном (корпускулярном) движении. Кроме тензора плотности на всех этапах вычислительного будут проявляться упругие и вязкостные свойства жидкости в виде связанных тензоров
связывается предыстория деформации элементарных расчетных объектов, что позволяет на лагранжевом этапе вычислительного эксперимента считать крупные частицы жидкости как участвующие в свободном (корпускулярном) движении. Кроме тензора плотности на всех этапах вычислительного будут проявляться упругие и вязкостные свойства жидкости в виде связанных тензоров 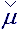 и
и 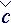 , реальные физические величины которых зависят от текущего состояния тензора формы
, реальные физические величины которых зависят от текущего состояния тензора формы  . Если же в вычислительном эксперименте используется модель идеальной жидкости на неподвижных узлах сетки Ω
. Если же в вычислительном эксперименте используется модель идеальной жидкости на неподвижных узлах сетки Ω i, то суть вычислений будет сводиться к обеспечению изотропности среды, когда тензоры
i, то суть вычислений будет сводиться к обеспечению изотропности среды, когда тензоры 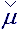 и
и 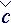 образуются только равными по величине диагональными компонентами.
образуются только равными по величине диагональными компонентами.
Свойства вычислительных операций и элементарных объектов
Все операции вычислительной гидромеханики выполняются исключительно в размерной форме, что в первую очередь необходимо для контроля физической корректности моделируемых процессов для каждой, отдельно взятой частицы жидкости, и обеспечения возможности эмпирической корректировки или применения гибридных схем в подобластях, где необходима автоматическая подмена математических моделей. С вычислительными объектами связываются три группы операций:
1. Операции логические или эмпирические. Это физические законы, такие как: если есть тензор конвективных скоростей  , то он порождает тензор напряжений
, то он порождает тензор напряжений  по закону (2), и т.п. Такие операции задают способ формирования и методы анализа состояния тензорных объектов, а также принятие решений об изменении математических моделей по ходу расчетов;
по закону (2), и т.п. Такие операции задают способ формирования и методы анализа состояния тензорных объектов, а также принятие решений об изменении математических моделей по ходу расчетов;
2. Операции типа сложение, применяются только к величинам с одинаковыми физическими размерностями и при условии, что они определены и построены в одном и том же базисе. К сложным объектам сложение может также применяться в условиях, когда определены операции автоматического согласования систем отсчета и физических размерностей;
3. Операция произведение применима только к объектам, у которых связываемые компоненты лежат в дуальных системах отсчета. Запрещается повышение ранга тензора в операциях произведения. Для построения векторных или тензорных объектов должны определяться специальные алгоритмы, опирающиеся на физическую постановку задачи о проведении вычислительного эксперимента.
Вычислительные объекты наделяются следующими свойствами:
1. Скалярные или инвариантные величины, например время t, могут участвовать только в операциях произведения, с любыми объектами.
2. Векторные величины участвуют в операциях сложения с сопоставимыми векторами и в операциях произведения с тензорами, если это необходимо для перехода из одной системы отсчета в другую. Применение умножения векторов для построения диад недопустимо.
3. Тензорные величины определяют физические свойства элементарных частиц жидкости, их геометрические деформации, кинематические свойства и другие динамические процессы в сплошной среде. Тензоры могут участвовать как в операциях сложения, с сопоставимыми тензорами, а также в операциях произведения со связанными векторными или скалярными объектами. С использованием тензорных объектов формулируются основные законы гидромеханики, а автоматическое конструирование и анализ этих объектов образует собственно и саму логико-математическую задачу о проведении вычислительного эксперимента в гидромеханике.
Движение контрольной точки в пространстве, сместившейся за один такт первого (эйлерового) этапа вычислительного эксперимента, может быть представлено как пересчет координат точки в локальной системе отсчета в абсолютную, с учетом интервала времени t :
+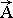 =
=  +
+  ·t +
·t + 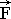 ·
·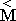 ·t2/2 + (
·t2/2 + ( +
+  ·t +
·t + 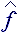 ·t2/2)·
·t2/2)·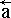 ( 4 )
( 4 )
Следующим этапом вычислений может быть определение вектора приращения локальной скорости для этой точки (ускорения), по полю которого затем восстанавливается новое поле внешних сил и внутренней энергии для исходных крупных частиц жидкости:
+ =
=  + (
+ (  +
+  ·t )·
·t )·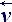 .
( 5 )
.
( 5 )
Таким образом выполняется первый шаг вычислительного эксперимента, за которым следует контроль корректности решения на поле { r }; согласование условий сохранения физических параметров внутри элементарных ячеек жидкости { M }; а в завершение – выполняется перерасчет новых для каждой крупной частицы жидкости «внешних сил»:
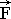 =
= 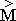 ·
· ·
· =
=  ·
· ·
· ·
· .
.
Схемой расщепления решения для уравнений второго порядка по физическим процессам, будем называть деление процесса вычислений на два этапа, на каждом из которых выполняется дифференцирование первого порядка. Если на одном из этапов выполняется пространственное дифференцирование поля скорости, то затем по нему вычисляется новое поле напряжений, что позволяет на втором этапе выполнить расчет смещений частиц жидкости по скорректированному ускорениями полю скорости, и с использованием конвективных перераспределений потоков согласовать условия сохранения, и снова восстанавливается поле скорости, но уже на новый момент времени.
Главная особенность пространственного дифференцирования состоит в том, что результат этой операции переносится с узлов расчетной области на центры тяжести крупных частиц жидкости, а эти центры смещаются в направлении скорости свободного движения частиц. Это означает, что второй этап вычислений усложняется дополнительными алгоритмами интерполяции внутри расчетной области и экстраполяции в разорванных узлах, на внешних границах этой области.
Если в задаче участвуют распределенные массовые силы, например в виде ускорения свободного падения, то они будут постоянно отклонять траекторию движения свободных частиц, которая на втором этапе должна выправляться за счет упругости жидкости. Для отключения такого механизма трансформации частиц жидкости, необходимо искать механизмы замены поля внешних сил напряженным состоянием свободной поверхности, к примеру.
Построение вычислительного эксперимента
Процесс трансформации полей, в случае исходного требования сохранения координат узловых точек { }, может быть разделен на три этапа:
}, может быть разделен на три этапа:
1 этап. КИНЕМАТИКА
– Новое поле узловых точек:
{+ =
=  +
+  ·t +
·t + 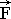 ·
·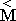 ·t2/2 }( 6 )
·t2/2 }( 6 )
– Поле конвективных скоростей образуется алгоритмическим построением тензора:
{  } = { +
} = { + i - Ω
i - Ω i
} ( 7 )
i
} ( 7 )
– Расчетное состояние нового поля внутренних свойств:
{ +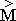 } = {
} = { ·+
·+ } = { (
} = { ( +
+  ·t)·
·t)· }
}
{+ } = {
} = {  ·(1+
·(1+ ·t) } ( 8 )
·t) } ( 8 )
2 этап. ДИНАМИКА
Здесь производится сопоставление реологии жидкости с текущим состоянием вычислительной модели. Пусть определен закон сохранения количества движения на разнесенном по этапам вычислений интервале времени:
+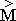 ·
· =
= 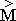 ·(
·(  +
D
+
D ), исходя из (8):
), исходя из (8):
Δ = ( +
= ( +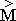 -
- 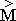 ) ·
) ·
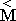 ·
· =
=  ·
· ·t, ( 9 )
·t, ( 9 )
получается уравнения Ньютона в форме Эйлера, справедливое на неподвижных узлах расчетной области:
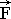 =
= 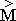 ·
· ·
· =
=  ·
· ·
· ·
· .
( 1* )
.
( 1* )
Полученное выражение содержит в себе напряженное состояние жидкости, которое можно объяснить реологическими свойствами вычислительной модели течения:
{ 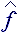 } = { +
} = { +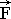 i - 0
i - 0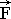 i } или
i } или
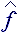 =
=  ·
· ·
· ·
· =
= 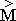 ·
· ·
· .
.
По форме новое уравнение соответствует записи напряжений в уравнениях Навье-Стокса. Реология реальной жидкости оформляется в виде законов (2),(3), связанных с тензором конвективных скоростей  . Тогда суть расчетов может быть сведена к согласованию реологии вычислительной и физической моделей жидкости.
. Тогда суть расчетов может быть сведена к согласованию реологии вычислительной и физической моделей жидкости.
В результате разностного дифференцирования, в выражении (9) была утеряна объемная составляющая ускорения, которая может быть получена при рассмотрении движения частицы с переменной массой, без учета деформации:
M = det( 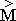 ),
),
r = det(  ),.
),.
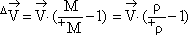 (10)
(10)
Рассматриваемая вычислительная модель всегда наделяет жидкость свойствами сжимаемости, вязкости и упругости. Ранее указывалось, что жидкость должна быть изотропной, так как не ведется отслеживание ориентации тензоров формы  . Выделением диагонального тензора, такого, что след от остатка будет равен 0, получим тензор шарового сжатия:
. Выделением диагонального тензора, такого, что след от остатка будет равен 0, получим тензор шарового сжатия:

 =
=  0 +
0 +  * :
tr(
* :
tr(  )=0,
)=0,  0 =
0 = 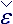 ·
· 0·t,
( 11 )
0·t,
( 11 )
где компоненты тензора  0 определяют давление,
0 определяют давление, 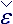 – коэффициент динамического сжатия.
– коэффициент динамического сжатия.Выделением кососимметричной части матрицы  , которая задает вращение одной крупной частицы относительно смежных, будет получен тензор вязких напряжений:
, которая задает вращение одной крупной частицы относительно смежных, будет получен тензор вязких напряжений:
 Н =
Н = 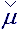 ·
· H =
H =
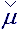 ·(
·(  * -
* -  * T)/2. ( 12 )
* T)/2. ( 12 )
Оставшийся симметричный тензор связывается с упругой деформацией (6):
 Г =
Г = 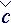 ·
· Г =
Г = 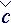 ·(
·(
 *-
*-  * T)·t/2. ( 13 )
* T)·t/2. ( 13 )
Полный тензор внутренних напряжений:  = (
= (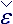 ·
· 0+
0+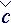 ·
· Г)·t/2 +
Г)·t/2 + 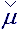 ·
· H. ( 14 )
H. ( 14 )
Рассматриваемые динамические коэффициенты 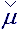 ,
, 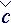 и
и 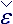 отличаются от кинематических, коэффициентом скалярной плотности r. Под действием тензора напряжений
отличаются от кинематических, коэффициентом скалярной плотности r. Под действием тензора напряжений  , частица получает приращение скорости внутреннего (замкнутого) движения:
, частица получает приращение скорости внутреннего (замкнутого) движения:
Δ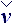 =
=  · t /ρ
( 15 )
· t /ρ
( 15 )
Если течение установившееся, то, за расчетный интервал времени, тензор приращения скоростей Δ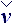 должен компенсировать сам тензор конвективных скоростей:
должен компенсировать сам тензор конвективных скоростей:  ·
·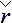 +
+ 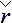 ·
D
·
D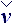 = 0.
= 0.
Последнее выражение является точным, если не учитывается смещение крупных частиц за время t.
3 этап. СТАТИКА
На завершающем этапе, необходимо провести восстановление поля скорости по вычисленным на втором этапе приращениям, при этом рассматриваются деформационные движения вокруг статических центров тяжести частиц.
От тензора Δ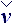 , определенного в локальном базисе, необходимо перейти к смешанному тензору, где локальные характеристики опираются на абсолютную систему отсчета:
, определенного в локальном базисе, необходимо перейти к смешанному тензору, где локальные характеристики опираются на абсолютную систему отсчета:
Δ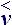 = Δ
= Δ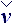 ·
· ,
( 16 )
,
( 16 )
этот тензор не связан с локальной геометрией базиса  .
.
Для перехода к исходной сетке построим новый локальный базис, который опирается на неподвижный узел, а в качестве смежных использует смещенные во времени пространственные точки:
 = ++
= ++ i - 00
i - 00 i,
( 17 )
i,
( 17 )
Раскрывая тензорное выражение (7):  = vij =
= vij = 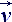 i
= +
i
= + i - Ω
i - Ω i, по скоростям связанным с новыми базисными векторами
i, по скоростям связанным с новыми базисными векторами 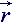 , получим алгоритм вычисления нового поля скорости:
, получим алгоритм вычисления нового поля скорости:
+ =
=  + Si*
+ Si* ·Δ
·Δ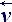 i
(18 )
i
(18 )
который суммирует приращения скорости от окружающих крупных частиц.
Выражения (15) - (18) раскрывают обратный закон Ньютона: 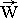 =
= 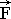 ·
·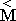 .
.
Ускорения полученные в векторной форме: для частицы с переменной "массой" (10); и для распределенных массовых сил, должны быть интерполированы с центров ячеек на исходные узлы расчетной области.
Словесно, этапы вычислений определяются следующим образом:
1 - на неподвижной Эйлеровой сетке производятся расчеты распределенных характеристик течения;
2 - рассматриваются внутренние свойства частиц жидкости, с целью построения тензоров "массы", в которых сохраняется предыстория деформации. Здесь же организуются итерационные процессы установления, в которых происходит согласование реологии вычислительной и физической модели течения жидкости;
3 - на завершающем этапе производится интерполяция характеристик течения со смещенных, в Лагранжевом движении центров тяжести крупных частиц, на исходные узлы расчетной области. На этом же этапе можно рассмотреть условия на свободных (жидких) границах, где вместо алгоритмов интерполяции в разорванных узлах нерегуляризованной сетки внутри расчетной области, будет использоваться экстраполяция с помощью заграничных центров особых (граничных) частиц жидкости.
Вычислительная среда
Свойства тензора напряжений 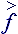 могут не соответствовать реологии рассматриваемой жидкости. Для получения итерационного алгоритма согласования физических и вычислительных параметров течения, тензор
могут не соответствовать реологии рассматриваемой жидкости. Для получения итерационного алгоритма согласования физических и вычислительных параметров течения, тензор 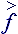 можно разделить на истинный тензор и девиатор. Это позволит допустимые напряжения включить в динамику течения, а девиаторные отразить от границ сопряжения смежных частиц, тем самым демпфируя дальнейшее развитие девиации. Соответственно корректируется тензор конвективных скоростей
можно разделить на истинный тензор и девиатор. Это позволит допустимые напряжения включить в динамику течения, а девиаторные отразить от границ сопряжения смежных частиц, тем самым демпфируя дальнейшее развитие девиации. Соответственно корректируется тензор конвективных скоростей  , из которого вычитаются девиационные компоненты. По сути, это обычный механизм свободных и отражающих границ, только он применяется к каждой частице.
, из которого вычитаются девиационные компоненты. По сути, это обычный механизм свободных и отражающих границ, только он применяется к каждой частице.
Если начальные условия, при запуске процесса решения, не соответствуют законам течения жидкости, то величина тензора девиации может быть настолько большой, что произойдет разрушение аппроксимационных критериев. В этом случае можно воспользоваться поправками к реологическим параметрам жидкости, которые методом итераций должны согласовать (или приблизить) физические и вычислительные характеристики течения. Последнее особенно касается идеализированных жидкостей, описание которых всегда будет сводится к итерационным процессам.
Контроль корректности выполняемого решения, в вычислительном плане, всегда сводится к контролю допустимости интерполяционных формул. В качестве примера разрушения решения, можно привести случай, когда одна грань частицы, в результате свободного движения в заданном поле скоростей, обгонит противоположную грань этой же частицы. Этого можно избежать уменьшением расчетного интервала времени. Выражение, показывающее предельный интервал, обычно называют критерием устойчивости решения во времени, в частности, известный критерий Куранта, в точности соответствует вышеуказанному определению. С контролем пространственной аппроксимации, по мнению автора, дело обстоит существенно сложнее, так как соответствующие критерии связываются не только с начальными условиями, но и с локальными геометрическими характеристиками расчетной области. Здесь можно предложить метод визуального контроля формы расчетных полей, после выполнения каждого такта вычислений во времени.
В соответствии с выражением (8): +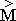 = (
= (  +
+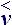 ·t )·
·t )· , масса частицы фактически является сумматором тензоров локальных скоростей. На первом этапе
, масса частицы фактически является сумматором тензоров локальных скоростей. На первом этапе 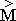 используется для определения внутренних свойств частицы, на третьем - с помощью
используется для определения внутренних свойств частицы, на третьем - с помощью 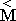 =
= 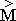 -1 описывается взаимодействие смежных частиц жидкости. Вычислительная модель всегда содержит в себе три основных свойства жидкости: сжимаемость; вязкость; упругость, при этом соотношение интенсивностей указанных напряжений, может привести к критическому режиму или изменить режим течения жидкости (имеется в виду образование струй, вихревых слоев и кавитационных разрывов).
-1 описывается взаимодействие смежных частиц жидкости. Вычислительная модель всегда содержит в себе три основных свойства жидкости: сжимаемость; вязкость; упругость, при этом соотношение интенсивностей указанных напряжений, может привести к критическому режиму или изменить режим течения жидкости (имеется в виду образование струй, вихревых слоев и кавитационных разрывов).
 =
= 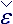 ·
· 0·t·+
0·t·+ 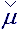 ·
· Н·+
Н·+
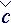 ·
· г·t·=
г·t·=  0 +
0 +  Н +
Н +  Г. ( 14*)
Г. ( 14*)
Тензор напряжений (14) можно определить в качестве характеристического полинома для внутреннего состояния частицы, где:
 0 : I ≠ 0 - сжимаемость;
0 : I ≠ 0 - сжимаемость;
 Н : II ≠ 0 - поворот;
Н : II ≠ 0 - поворот;
 г : III ≠ 0 - чистая деформация, другие инварианты этих тензоров равны нулю.
г : III ≠ 0 - чистая деформация, другие инварианты этих тензоров равны нулю.
Если внутреннее состояние частицы рассматривается без учета смещения расчетных узлов, то можно поставить требование компенсации тензора локальных скоростей, за счет приращений скорости вызываемых тензором напряжений:
 ·t +
·t + 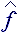 ·
· ·t2/2 = 0, ( 19 )
·t2/2 = 0, ( 19 )
из которого, в качестве сумматора напряжений можно вывести тензорную плотность:
+ =
=  + (
+ (  0 +
0 +  Н +
Н +
 Г.)·t2/2 @
Г.)·t2/2 @  0 +
0 +  Н +
Н +  Г. ( 20 )
Г. ( 20 )
Рассмотрим два варианта разрушения тензора + Н, когда ρ = det(
Н, когда ρ = det(  ) обращается в ноль.
) обращается в ноль.
1. Кавитационный разрыв плотности:
 Н - не рассматривается;
Н - не рассматривается;
ρ0 = det(  0 ) < 0 - соответствует полю с разрежением;
0 ) < 0 - соответствует полю с разрежением;
ρ* = det(  0+
0+  г ) = 0 - тензор плотности обращается в диаду, которая может быть определена плоскостью, перпендикулярной к главной оси растяжения тензора упругости
г ) = 0 - тензор плотности обращается в диаду, которая может быть определена плоскостью, перпендикулярной к главной оси растяжения тензора упругости  г. Если жидкость не выдерживает отрицательного давления, то данная плоскость должна быть использована в качестве свободной границы, проходящей через крупную частицу.
г. Если жидкость не выдерживает отрицательного давления, то данная плоскость должна быть использована в качестве свободной границы, проходящей через крупную частицу.
2. Образование свободной струи или турбулентного вихря.
 Пусть система отсчета будет связана с движущейся частицей, которая подвержена сдвиговой деформации.
Пусть система отсчета будет связана с движущейся частицей, которая подвержена сдвиговой деформации.На завершающем этапе вычислений, исходная вихревая частица может обратить в ноль детерминант внутреннего поля сопряженной частицы, где ρo
> 0. В этом случае можно воспользоваться эмпирическим алгоритмом переноса вихря с первого этапа вычислений, в тензор "массы" третьего этапа. В этом случае будет снято напряжение со смежной ячейки, а частица в свободном движении будет проявлять особенности свойственные турбулентному вихрю. Приведенный алгоритм является эмпирической моделью, которую можно использовать за пределами аппроксимационного разрешения расчетной области, для получения точного решения, сетка в районе вихря может быть сгущена.
Простые примеры эффективной численной реализации метода
Тензорная арифметика, использованная для проектирования полных и прямых вычислительных экспериментов в гидромеханике, в общем случае всегда имеет дело с реальными жидкостями, обладающими полным комплексом реологических свойств, которые задаются линейными/обратными зависимостями в малом объеме. Основные иллюстрации выполнялись на примере решения гиперболической задачи о распространении упругих продольных волн (длинных волн в океане), которые допускают явные пространственные решения и, потому, очень удобны для физической интерпретации основных вычислительных процессов.
1. Однако даже простая реализация вычислительных экспериментов о распространении длинных волн в океане, построенная на основе тензорной модели, при реальном моделировании длинноволновых процессов в океане (приливы, штормовые нагоны, цунами) показывает хорошее соответствие модели натурным наблюдениям. Тензорная модель обладает ярко выраженными дисперсионными свойствами (увеличение периода при движении волны над неровным дном, или – так называемое «красное смещение»); эта модель показывает хорошее согласование с наблюдениями за временем затухания длинноволновых процессов вблизи побережья (декремент затухания
характеризует корректность условий сохранения энергии длинноволновых процессов); в случае успешного согласования аппроксимационных критериев в вычислительной модели, получается хорошее соответствие формы и порядка следования длинноволновых импульсов моделируемого и реального цунами вблизи мелководных участков побережья (корректное протекание интерференционных, дисперсионных и рефракционных процессов для волновых процессов). При использовании полной длинноволновой модели, в которой задействуется «конвективное» перемешивание частиц жидкости, такая модель позволяет создавать вычислительные эксперименты с «сильно нелинейными свойствами», в том числе моделировать накат волны на пологий берег, а также задействовать гибридные схемы и эмпирические методы, к примеру для учета обрушения волн.
Аналогичные результаты не могут быть получены традиционными методами аналитического или численного решения классических систем дифференциальных уравнений гидромеханики в частных производных.
2. Важным подтверждением корректности тензорных уравнений служи вычислительный эксперимент по моделированию обтекания нескольких тел произвольной формы потоком идеальной жидкости (т.е. потоком, внутри которого отсутствуют вихреисточники).
Главной особенностью идеальной жидкости является то, что все показанные здесь тензорные законы справедливы по отношению не только к смежным крупным частицам жидкости, но по аналогии с законом «Био-Савара» динамика частиц жидкости должно удовлетворять условиям дальнего взаимодействия, которое осуществляется по не искривленным лучам, и без искажения линейных/обратных законов взаимодействия с расстоянием. Это означает, что моделирование обтекания тел идеальной жидкостью должно сводится к простому интегрированию твердого тела по объему и поверхности. Для этого объем твердого тела должен быть наполнен диполями, а поверхность вихреисточниками. Тензоры-диполи должны обладать энергией для захвата объема жидкости и перемещения его с заданной скоростью, а каждый вихреисточник должен обладать той же интенсивностью, что и тензорный диполь, а его соотношение вихревой и излучающей части должно обеспечивать локальное искажение внешнего потока так, чтобы он в секторе вихреисточника был сориентирован вдоль границы тела.
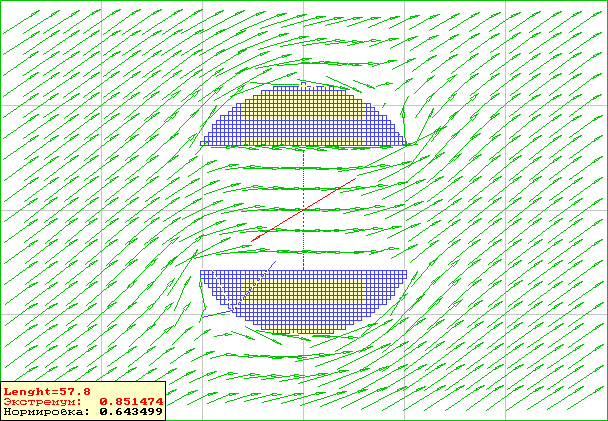
Пример решения задачи об обтекании двух тел косым потоком, где параметры течения вычисляются простым интегрированием по объему и поверхности тел
Заключение
Изложена идея связи между численным описанием частиц жидкости конечного объема (крупных частиц жидкости) и реологическими параметрами жидкости, которые оказались жестко и однозначно связанными с гидродинамическими процессами внутри контрольного объема новой вычислительной модели. Концептуально показаны методы анализа качества вычислительной модели. Любопытным теоретическим исследованием в будущем может быть анализ характеристического разложения тензора напряжений по реологическим законам, энергетические оценки которого связаны с режимами течения реальной жидкости.
Установлено, что в процессе проведения вычислительного эксперимента осуществляется согласование свойств тензорных объектов с заданными моделями течений. Кроме традиционного контроля условий неразрывности, в новой модели всегда требуется согласование условий упругости, вязкости и других, в том числе анизотропных проявлений вычислительных объектов. Ввиду общности подхода, такая постановка гидромеханической задачи может привести к довольно сложным реализациям вычислительных экспериментов, однако, все же, это является достоинством метода, так как позволяет постоянно держать под полным контролем как ход вычислительных процессов, так и весь комплекс реологических свойств моделируемой среды. В результате упрощения модели до уровня идеальной жидкости был разработан и успешно протестирован алгоритм расчета обтекания группы тел, который сводится к простому интегрированию по их объему и поверхности.
Практическое использование тензорной модели опирается на представление главных законов механики и реологических свойств жидкости в обобщенной тензорной форме. Важным достоинством новой модели является также то, что без потери общности практически все математические записи доведены до уровня простых арифметических выражений.
Литература
1. Астарита Дж., Маруччи Дж. Основы гидромеханики неньютоновских жидкостей, М., Мир, 1978. – 307 с.
2. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. - М.: Наука, 1982. 370с.
3. Бернар Ле Меоте Введение в гидромеханику и теорию волн на воде. Л.: Гидрометеоиздат, 1974. – 367 с.
4. Годунов С.К. Элементы механики сплошной среды, М: Наука, 1963, 303с.
5. Мак-Коннел А.Дж., Введение в тензорный анализ, М.: Наука, 1963, 411с.
6. Самарский А.А., Попов Ю.П., Разностные методы решения задач газовой динамики, М.: Наука, 1980, 352с.
7. Филин А.Н., Прикладная механика твердого деформируемого тела, Т.1, М.: Наука, 1975, 832с.
8. Храмушин В.Н. О постановке вычислительного эксперимента в гидромеханике. Реализация задачи о распространении длинных волн: Препринт. - Южно-Сахалинск: ИМГиГ ДВО АН СССР, 1988. - 41с.
 Оглавление
Оглавление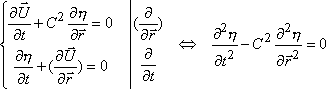 ,
,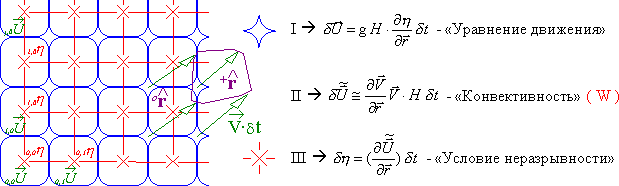
 Формально векторный Закон Ньютона может быть построен с помощью тензорной операции умножения, где внешняя сила
Формально векторный Закон Ньютона может быть построен с помощью тензорной операции умножения, где внешняя сила 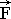 задается в абсолютной системе координат, а реакция
задается в абсолютной системе координат, а реакция 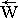 – уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы
– уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы  будет исполнять роль не только аккумулятора энергии поступательного движения, но также учтет инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
будет исполнять роль не только аккумулятора энергии поступательного движения, но также учтет инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.


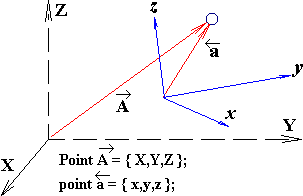 Геометрически частица жидкости {
Геометрически частица жидкости { /
/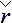 } может быть представлена в виде
параллелепипеда / эллипсоида, внутреннее состояние которого формализуются линейными / обратными распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных / локальных базисов (трехмерных тензоров II ранга), задающих линейное/обратное распределение внутренних свойств течения между жидкими частицами, которые однозначно связаны интерполяционными (без экстраполяции) зависимостями с исходными узлами расчетной области.
} может быть представлена в виде
параллелепипеда / эллипсоида, внутреннее состояние которого формализуются линейными / обратными распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных / локальных базисов (трехмерных тензоров II ранга), задающих линейное/обратное распределение внутренних свойств течения между жидкими частицами, которые однозначно связаны интерполяционными (без экстраполяции) зависимостями с исходными узлами расчетной области.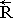 измеряется в локальной системе отсчета, связанной с текущим состоянием и местоположением крупной частицы жидкости.
измеряется в локальной системе отсчета, связанной с текущим состоянием и местоположением крупной частицы жидкости.
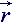 i =
+
i =
+ i - Ω
i - Ω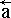 =
= 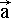 – вектор переходит из абсолютной в локальную систему координат. Для перестройки вектора из локальной системы отсчета к абсолютной – необходимо добавить координаты базовой точки крупной частицы жидкости:
– вектор переходит из абсолютной в локальную систему координат. Для перестройки вектора из локальной системы отсчета к абсолютной – необходимо добавить координаты базовой точки крупной частицы жидкости: 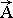 =
=
 = +
= +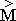 } [кг] – тензорное поле внутренних свойств частицы.
} [кг] – тензорное поле внутренних свойств частицы. [м3/c] – тензор локальных (конвективных) скоростей;
[м3/c] – тензор локальных (конвективных) скоростей;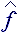 [Н·м2] – тензор напряжений.
[Н·м2] – тензор напряжений.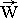 ; (1)
; (1) Н =
Н = 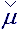 ·
· =
= 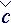 ·(1+
·(1+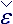 ·
· Здесь снова строчными буквами обозначены вычислительные объекты, заданные в локальных координатах конкретных частиц жидкости, а прописными – формализованные функции, определенные в абсолютной системе координат. Обозначения:
Здесь снова строчными буквами обозначены вычислительные объекты, заданные в локальных координатах конкретных частиц жидкости, а прописными – формализованные функции, определенные в абсолютной системе координат. Обозначения: 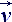 i = +
i = + = rij·ρ jk – тензор инерции (масса) в проекции на абсолютную систему отсчета;
= rij·ρ jk – тензор инерции (масса) в проекции на абсолютную систему отсчета; 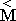 ·t2/2 + (
·t2/2 + (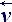 .
( 5 )
.
( 5 )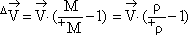 (10)
(10) 
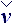 =
= 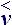 = Δ
= Δ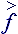 могут не соответствовать реологии рассматриваемой жидкости. Для получения итерационного алгоритма согласования физических и вычислительных параметров течения, тензор
могут не соответствовать реологии рассматриваемой жидкости. Для получения итерационного алгоритма согласования физических и вычислительных параметров течения, тензор  Пусть система отсчета будет связана с движущейся частицей, которая подвержена сдвиговой деформации.
Пусть система отсчета будет связана с движущейся частицей, которая подвержена сдвиговой деформации.