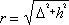, коэффициенты m, p, q - эмпирические константы, которые для Курильских островов равны соответственно 1.5, 4.5, 4.5 [Новый каталог..., 1977]. Сила сотрясений в эпицентре землетрясения (=0)Как известно, минимальная информация о землетрясении, по которой, как правило, осуществляется оперативный прогноз цунами, включает в себя данные о положении его эпицентра и магнитуде. Широко известные корреляционные соотношения, связывающие магнитуду землетрясения и высоту волн цунами на ближайшем побережье или их интенсивность (эти и другие подобные соотношения приводятся и детально обсуждаются, в частности, в [Соловьев, 1972, Го, 1987]) не используются в практике оперативного прогноза цунами из-за большого рассеивания коррелируемых величин. В этой главе мы получаем несколько формул для прогноза начальной высоты цунами на ближайших к источнику берегах по известным положению эпицентра землетрясения, магнитуде и глубине очага землетрясения, используя и развивая предположение о связи макросейсмического эффекта землетрясения (интенсивности сотрясений в эпицентральной области) с его цунамигенностью.
Из определения понятия интенсивности цунами [Соловьев, 1972] непосредственно вытекает, что эта величина характеризует цунами аналогично тому, как ощущаемость сотрясений, выраженная в единицах соответствующей макросейсмической шкалы, характеризует землетрясение. (И интенсивность цунами, и интенсивность сотрясений при землетрясении пропорциональны логарифму, соответственно, максимального или среднего заплеска волны цунами на ближайшем к источнику побережье и максимальной амплитуды смещения, скорости или ускорения в сейсмической волне).
В работе [Поплавская, 1977] показано, что источники опасных волн цунами с интенсивностью i і0, возникающих в пределах Курило-Камчатской эпицентральной зоны, представляют собой область сотрясений не менее 9 баллов по шкале MSK-64 и оконтуриваются наилучшим образом, соответственно, изосейстой 9-10 балла. Таким образом достаточно убедительно обосновывается предположение о тесной связи между способностью землетрясения вызвать волны цунами большой интенсивности и силой сотрясений в пределах его эпицентральной области. При этом в качестве порога цунамиопасности землетрясения по максимальной балльности было бы естественно принять значение J0 = 9 баллов.
Максимальный балл сотрясений при землетрясении определяется двумя основными параметрами - магнитудой M и глубиной очага h. Если принять, что цунами есть не что иное, как специфический макросейсмический эффект подводного землетрясения, то естественно предположить, что и упомянутое выше большое рассеивание, характерное для корреляционных соотношений, связывающих магнитуду землетрясения и интенсивность цунами, обуславливается не только стохастической природой этой связи, но и детерминированным влиянием не учитываемого параметра - глубины очага. Не углубляясь в вопросы физического содержания такой связи, можно попытаться использовать уже существующие формулы макросейсмического поля для получения самого раннего прогноза высоты волны цунами на ближайших к источнику берегах.
В работе [Соловьев, 1972] в числе многих других исследуется вопрос о "вероятности возбуждения цунами землетрясением произвольной магнитуды". Фактически речь идет о форме интегрального распределения магнитуды цунамигенных землетрясений и показывается, что она удовлетворительно аппроксимируется нормальной кривой. В случае землетрясений, принадлежащих эпицентральным зонам, примыкающим к островным дугам со стороны океана, ее параметры имеют значения: M =7.75, s =0.25. При этом вероятность возбуждения цунами землетрясением близка к нулю при магнитуде 7 или менее и - к единице при магнитуде 8.5 или более.
Если принять, что волны цунами возникают лишь при достижении определенной интенсивности сотрясений в эпицентре J0 і Jt, то вероятность возникновения цунами должна совпадать с вероятностью возникновения в эпицентре таких сотрясений. Последняя, как функция магнитуды, может быть оценена при различных значениях Jt для той или иной эпицентральной зоны независимо. Совпадение ее при каком-то фиксированном значении Jt с кривой распределения магнитуд цунамигенных землетрясений явится дополнительным подтверждением существования связи между цунамигенностью землетрясения и интенсивностью сотрясений в его эпицентре. При этом определится и значение макросейсмического порога цунамигенности (цунамиопасности).
Интенсивность сотрясений J при тихоокеанских землетрясениях вблизи Курильских островов выражается через магнитуду M, глубину очага h и эпицентральное расстояние следующим образом
J = mM - p ×lg r + q, (4.1)
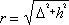, коэффициенты m, p, q - эмпирические константы, которые для Курильских островов равны соответственно 1.5, 4.5, 4.5 [Новый каталог..., 1977]. Сила сотрясений в эпицентре землетрясения (=0)
Jo = mM - p×lg h + q, (4.1a)
Положив J0Jt и используя последнее соотношение, получим условие, которому должны удовлетворять магнитуда и глубина очага землетрясения, чтобы максимальный балл сотрясений в его эпицентре был не ниже Jt:
mM - p×lg h + q і Jt . (4.2)
При фиксированной магнитуде из последнего условия определяется интервал глубин очага землетрясения, ему удовлетворяющий
0 < h Ј hmax(4.3)
где lg hmax = (mM - Jt + q) / p. (4.4)
Если теперь предположить, что землетрясение любой магнитуды может произойти на любой глубине в области их существования с равной вероятностью, то вероятность того, что сила сотрясений в эпицентре землетрясения c магнитудой M будет не ниже Jt должна совпасть с вероятностью попадания его фактической глубины в интервал (4.3). Последнюю можно оценить, воспользовавшись каким-либо выборочным эмпирическим распределением глубин.
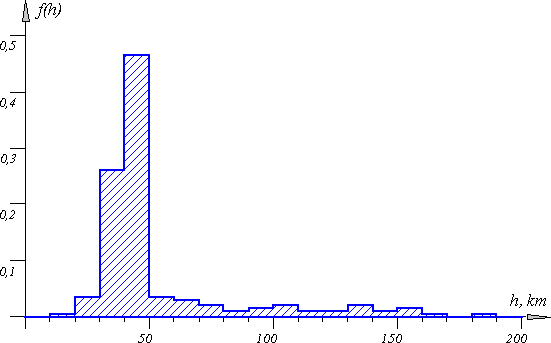
Рис. 101.Гистограмма плотности эмпирического распределения глубин очагов Курило-Охотских землетрясений, происшедших в 1987 году на глубинах h < 200 км.
В качестве исходной для дальнейших расчетов нами была взята выборочная функция распределения глубин очагов Курило-Охотских землетрясений, происшедших в 1987 году, по данным ежегодника [Землетрясения с СССР в 1987 году, 1990], показанная на рис.101.
Она построена с шагом Dh=10 км (использование меньшего шага нецелесообразно из-за недостаточной точности определения этой величины). Абсолютное большинство Курило-Охотских землетрясений происходит на глубинах менее 100 км. Распределение глубин в этом интервале чрезвычайно устойчиво и имеет ярко выраженный максимум на глубинах 40 Ј h < 50 км, сохраняющийся на протяжении всего периода инструментальной регистрации землетрясений в этом районе.
Вероятность попадания глубины очага в интервал h Ј hmax(M, Jt), при фиксированных M и Jt, оценивалась как отношение числа событий, удовлетворяющих этому (4.3) условию к полному числу событий, имевших место на глубинах h Ј hmax (M = 8.75, Jt). Таким образом оценивалась условная вероятность попадания глубины очага землетрясения в тот или иной интервал, удовлетворяющий условию (4.3), при условии, что его глубина оказалась меньше предельной для выбранного значения Jt при максимальной возможной магнитуде. В случаях, когда правые границы этих интервалов не совпадали с целым числом шагов Dh дискретизации эмпирического распределения, доля событий, приходящихся на интервал dh < Dh, принималась пропорциональной отношению длин этих интервалов.
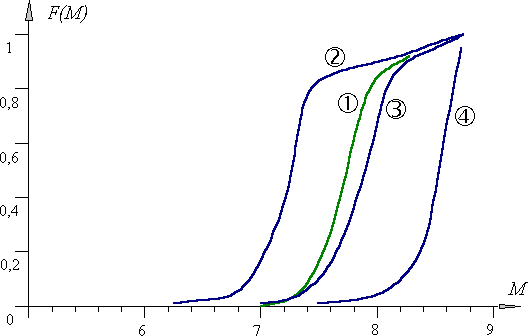
Рис. 102. Интегральная функция распределения магнитуд цунамигенных землетрясений, происходящих в районах островных дуг [Соловьев, 1972] - (1) и интегральные функции вероятности достижения в эпицентре сотрясений силой не менее 8 - (2), 9 - (3), 10 - (4) баллов.
На рис.102 показаны полученные таким образом вероятности достижения в эпицентре сотрясений силой J0 Ј Jt при трех значениях Jt = 8, 9 и 10 баллов. Там же показана нормальная кривая "вероятности возбуждения землетрясением произвольной магнитуды" (интегральная функция распределения магнитуды цунамигенных землетрясений) из [Соловьев, 1972]. Наилучшее согласие этой кривой с зависимостью P (M/J0 і Jt) достигается, когда Jt = 9 баллов.
Таким образом, выводы [Поплавская, 1980] о связи цунамигенности (цунамиопасности) подводных землетрясений с максимальной интенсивностью сотрясений, вызываемых ими в эпицентральной области, получили независимое подтверждение.
Воспользуемся теперь корреляционными соотношениями [Соловьев, 1972], связывающими интенсивность цунами со средней высотой волны вблизи источника h и с магнитудой землетрясения:
i = 0.5 + log2 h,(4.5)
i = 2.58 M - 19.2, (4.6)
а также логарифм энергии цунами Et (измеряемой в джоулях) с его интенсивностью
lg Et = 13.5 + 0.78 i. (4.7)
Исключая, формально, из приведенных соотношений интенсивность цунами, получим выражения связи средней максимальной высоты и энергии цунами в зависимости от магнитуды землетрясения:
lg h =0.78M - 5.93,
lg Et = 2M - 1.5. (4.8)
Пользуясь приведенными соотношениями мы можем оценить значения средней высоты волны, интенсивности и энергии цунами, соответствующие центру распределения магнитуд цунамигенных землетрясений: i = 0.8, h = 1.2 м, logEt=14. Из формулы (4.4) находим соответствующую максимальную глубину очага, при которой сила сотрясений составляет не менее 9 баллов, - hmax = 38 км. Это значение хорошо согласуется со значением наивероятнейшей глубины очага в Курило-Камчатской эпицентральной зоне равным 40 км. На этом основании мы делаем предположение о том, что форма начального возвышения в источнике цунами определяется, в основном, интенсивностью сотрясений в эпицентральной области землетрясения и что значительные отклонения наблюдаемых высот волн вблизи источника и интенсивности цунами от средних при фиксированной магнитуде объясняются, прежде всего, влиянием глубины очага землетрясения. Формулы же (4.8) могут быть использованы для самого раннего прогноза высоты вблизи источника и энергии цунами. При этом необходимо помнить, что они будут относиться к наиболее вероятной для островных дуг глубине очага землетрясения.
В макросейсмических исследованиях используются представления о макросейсмическом источнике, как области максимальных сотрясений в виде эллипса, размеры полуосей которого a0, b0 согласно [Поплавская, 1977] определяются через длину разлома в очаге землетрясения l0 и его магнитуду и глубину следующими корреляционными формулами. Длина разлома l0 в очаге землетрясения
lg l0 = 0.5M - 1.8, (4.9)
большая и малая полуоси эллипса
a0 = (l0 + 2h) / 2
b0 = h. (4.10)
И максимальный балл сотрясений силой J0 приписывается каждой точке площади, ограниченной рассматриваемым эллипсом. Если мы допустим, что основная часть начальной энергии цунами сосредоточена в пределах определенной формулами (4.9), (4.10) области, при условии, что J0 і 9, а начальное возвышение представляет собой половину эллипсоида с полуосью c0, опирающегося на этот эллипс, то получим возможность оценить начальную высоту цунами (воспользовавшись формулой для потенциальной энергии эллипсоидального возвышения) как:
, (4.11)
где r- плотность воды, а g - земное ускорение. Подставляя в эту формулу значения Et, a0, b0, соответствующие центру распределения магнитуд цунамигенных землетрясений (M = 7.75, hmax = 38 км), получим значение c0 = 1.9 м, которое несколько больше полученной выше оценки высоты волны на берегу вблизи источника (в источнике) h = 1.2 м. Это связано с тем, что, при вычислении c0, мы предполагали, что вся начальная энергия цунами сосредоточена в пределах площадки, ограниченной эллипсом с полуосями a0, b0, по-видимому, не совсем правильно.
На основании вышеизложенного можно рекомендовать два варианта быстрой оценки опасности цунами для ближайших к источнику побережий Курильских островов и, возможно, Камчатки и Приморья в случае возникновения местного сильного землетрясения. Первый вариант - оценка средней высоты цунами по первой из формул (4.8) для наиболее вероятного значения глубины очага землетрясения h=40 км. Второй - оценка c0 из (4.11), где в качестве глубины очага (в формулах (4.10)) следует принимать максимальную при данной магнитуде “цунамиопасную” глубину, вычисляемую по (4.4), где, в свою очередь, Jt принимается равным 9 баллам.
Наконец, пользуясь имеющимися вычислительными средствами и соответствующими программами, можно промоделировать процесс распространения цунами от эллипсоидального источника, параметры которого определяются соотношениями (4.9) - (4.11) и, тем самым, дать прогнозную оценку высоты волны цунами в конкретных населенных пунктах.
Приняв гипотезу о том, что цунами есть макросейсмический эффект землетрясения, естественно далее предположить, что связь между начальной высотой и формой начального возвышения в источнике цунами с основными макросейсмическими параметрами землетрясения имеет непрерывный характер. На основании аналогии формул (4.1), (4.1а) и (4.5)-(4.7), выражающейся в том, что безразмерные характеристики очага землетрясения и источника цунами (магнитуда, интенсивность сотрясений, интенсивность цунами) линейно связаны с логарифмами размерных величин (глубина очага, эпицентральное расстояние, высота и энергия волны цунами), мы предполагаем, что логарифм высоты начального возвышения в произвольной точке акватории пропорционален интенсивности сотрясений дна в той же точке:
lg h = A + BJ. (4.12)
Максимальная высота начального возвышения (в эпицентре), соответственно, равна
lg h0 = A + BJ0. (4.12а)
Тогда, с учетом (4.1), общий вид зависимости начальной высоты цунами от магнитуды и глубины очага землетрясения неизбежно будет следующим
lg h = a - blg r + kM, (4.13)
где a = A + Bq, b = Bp, k = Bm неизвестные нам коэффициенты, содержащие эмпирические макросейсмические константы m, p и q, r - гипоцентральное расстояние точки, M -магнитуда землетрясения. Максимальная высота волны будет соответствовать максимальным сотрясениям, когда r = h глубине очага землетрясения:
lg h0 = a - blg h + kM. (4.13а)
В координатах последняя будет представлять собой совокупность параллельных прямых с угловым коэффициентом k, начальная ордината которых определяется глубиной очага.
Значения неизвестных коэффициентов естественно определять из соответствующих данных наблюдений, наиболее доступная для нас сводка которых содержится в [Го, 1987]. Она составлена по данным известных каталогов и ряда индивидуальных описаний цунами (ссылки можно найти в самой работе) и отличается от аналогичных сводок других авторов тем, что в ней в качестве величины, характеризующей интенсивность цунами взят средний логарифм высоты заплеска цунами на ближайших к источнику берегах в отличие от логарифма среднего значения высоты заплеска, как это делалось ранее. Как убедительно показывает автор цитируемой работы, именно эта величина ("средне-логарифмическая высота") является несмещенной оценкой высоты начальной денивелляции уровня в источнике цунами. Это обстоятельство было последовательно учтено автором при определении максимального возвышения в источниках и энергии индивидуальных цунами. Сводка содержит данные о 56 цунами, проявившихся на побережьях Японии и Курильских островов (рис.103а, в виде точек).
Эта сводка, как впрочем и другие аналогичные, не содержит данных о глубинах очагов землетрясений, поэтому мы использовали не стандартную (и не вполне строгую) процедуру при отыскании коэффициентов в выражении (4.13а).
Так, в дальнейшем анализе эмпирических данных нами существенно использованы следующие, достаточно сильные допущения. Во-первых, мы полагаем, что произвольная выборка данных наблюдений h0 (M) является случайной выборкой реализаций зависимостей вида (4.13а), где глубина очага неизвестна, но подчинена закону распределения типа изображенного на рис.101 с наиболее вероятным значением глубины очага землетрясения, близким к его среднему выборочному значению h = 40км. Во-вторых, мы допускаем, что именно глубина очага, а не случайные ошибки оценок магнитуды и высоты цунами в источнике, является главной причиной рассеивания эмпирических точек. При сделанных допущениях наилучшей аппроксимацией зависимости вида (4.13а) для наиболее вероятной глубины h = 40 км будет ортогональная регрессия [Линник, 1958] между переменными h0 и M, построенная по всем данным выборки (ортогональная регрессия это прямая, отыскиваемая из условия минимума суммы квадратов расстояний эмпирических точек от искомой прямой вдоль нормали к ней). Угловой коэффициент такой регрессии, будет оценкой углового коэффициента k в выражении (4.13а) и другие коэффициенты этого выражения можно получить из очевидных соотношений (которые выводятся из выражений (4.12) - (4.13а)):
b = kp / m, a = lgh0 + blg 40 - kM, (4.14)
где lgh0 и M средние выборочные значения соответствующих переменных.
Действуя по вышеописанной схеме, с использованием эмпирического материала, содержащегося в [Го, 1987], мы получили следующие значения искомых коэффициентов: a= -4.307, b = 4.356, k = 1.452 и зависимость начальной высоты цунами от магнитуды и глубины очага для Курило-Японских землетрясений будет выглядеть так
lg h0 = - 4.307 - 4.356lg h + 1.452M, (4.15)
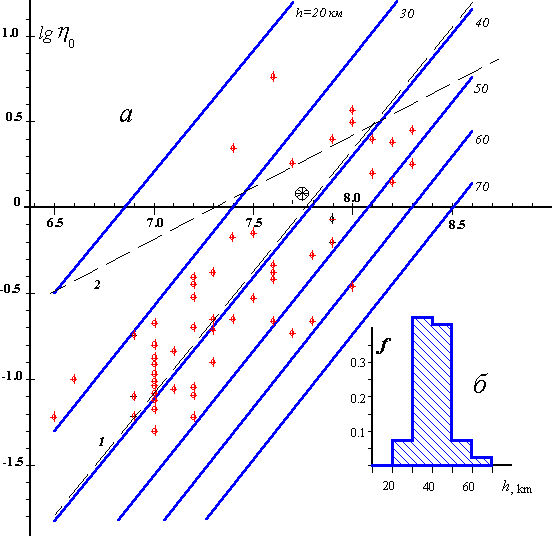
Рис.103 а. Эмпирические данные о (средне-логарифмических) высотах цунами в источнике в зависимости от магнитуды землетрясения и аппроксимирующие зависимости вида (4.15) для значений глубины h = 20, 30, 40, 50, 60 и 70 км. В качестве опорной зависимости log h0 (M, h = 40 км) принята прямая ортогональной регрессии, коэффициенты которой найдены по всем приведенным на рисунке эмпирическим данным для которых M і 7.0. Точка в виде звездочки отвечает среднему значению магнитуды и соответствующей высоты в источнике цунами в независимой выборке, использованной в [Соловьев, 1972]. Пунктирная линия (1) представляет зависимость (4.15), соответствующую значениямMh0 = 1.2, h = 38 км. Пунктирная линия (2) представляет зависимость с0[M, hmax(M)], полученную по формулам (4.4), (4.8) (4.11).
б. Гистограмма функции плотности распределения глубин очагов землетрясений, представленных на рис.4.3а в виде точек, при условии справедливости соотношений (4.15).
Найденная зависимость изображена на рис.103а в виде совокупности сплошных прямых линий, соответствующих глубинам h = 10, 20, 30, 40, 50, 60 и 70 км. Напомним, что прямая для h = 40 км есть прямая ортогональной регрессии, построенная по всем данным (для землетрясений с магнитудой M і 7.0).
Проконтролировать справедливость этой зависимости на имеющемся у нас материале наблюдений (когда глубины очагов землетрясений нам неизвестны, но известен только вид их функции распределения) мы можем лишь косвенно следующим образом.
Во-первых, у нас есть среднее значение магнитуды M = 7.75 цунамигенного землетрясения, найденное по независимому материалу наблюдений для островных дуг в [Соловьев, 1972] и соответствующее ему, согласно первой формуле (4.8) значение h0 = 1,2 м, не совпадающие с соответствующими средними значениями использованной здесь выборки [Го, 1987] (MГо = 7.5, lgh0,Го = -0.40). Если, однако, центр распределения неизвестных нам глубин очагов землетрясений в выборке, использованной в [Соловьев, 1972], приходится на значение h = 40 км, а коэффициент при M в (4.15) соответствует действительности, то точка с вышеуказанными координатами должна лежать на прямой вида (4.15) для h = 40 км или достаточно близко к ней.
Во-вторых, при тех же условиях, что и выше, зависимость вида (4.15), построенная для M = 7.75, h0 = 1.2 м и глубины h = 38 км должна быть близкой к искомой ортогональной регрессии.
В-третьих, зависимости вида (4.15) позволяют легко рассортировать эмпирические точки по предполагаемым глубинам очагов. Получающееся распределение, изображенное на рис.103б, должно иметь те же главные особенности, что и распределение на рис.101.
Как это можно видеть из приведенных рисунков все три требования хорошо удовлетворяются. Это позволяет надеяться на то, что изложенные в данном разделе представления о связи макросейсмической интенсивности землетрясения и максимальной высоты цунами в источнике достаточно близки к действительности, и формулу (4.15) также можно использовать в оперативной работе службы предупреждения о цунами.
Будем полагать, что разлом в сейсмическом очаге представляет собой вытянутый горизонтально прямолинейный отрезок длиной l, располагающийся на глубине h под поверхностью земли, а сила сотрясений в произвольной точке поверхности земли определится исключительно влиянием ближайшей к ней точки разлома. Введем прямоугольную систему координат x,y с началом в середине проекции отрезка l на земную поверхность, ось Ox направим параллельно этому отрезку, а ось Oy перпендикулярно ему. В этом случае максимальная высота начального возвышения в источнике цунами, согласно нашей гипотезе, будет определяться выражением (4.13), в котором аргумент r связан с только что введенными координатами x, y соотношениями
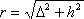, (4.16)
где D= ± y при -l /2 Ј x < l /2
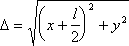при x < - l /2
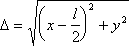при x і l /2.
Здесь - горизонтальное расстояние между текущей точкой плоскости и ближайшей к ней точкой разлома (эпицентральное расстояние текущей точки плоскости).Форма изолинии начальной высоты цунами показана на рис.104. Максимального значения h0, определяемого соотношением (4.13а), высота начального возвышения достигает на отрезке -l /2 Ј x < l /2, y = 0.
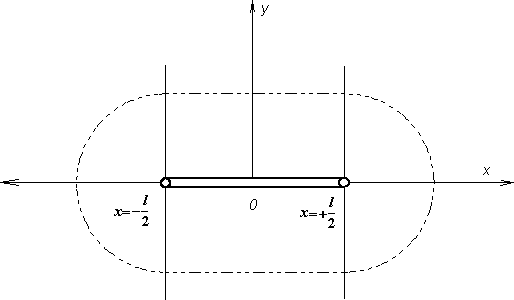
Рис. 104. Форма изолинии начальной высоты в макросейсмическом источнике. Площадь горизонтального сечения источника, очевидно, равна S = 2lD + pD2.
Из соотношений (4.13, 4.13а) легко получаем зависимость начального возвышения, отнесенного к максимальному, от эпицентрального расстояния D/h.
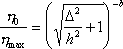(4.17)
Эта зависимость показана на рис.105.
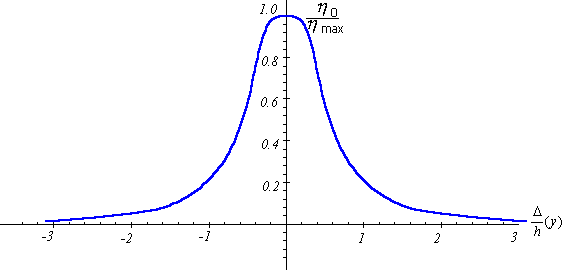
Рис.105.Зависимость относительной высоты начального возвышения h0 / hmax в макросейсмическом источнике цунами от относительного эпицентрального расстояния D / h.
Пользуясь последним выражением можно оценить энергию цунами как потенциальную энергию такого возвышения в виде
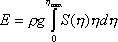, (4.18)
где r- плотность воды, g - ускорение силы тяжести и S = 2lD + pD2 - площадь горизонтального сечения начального возвышения (см. рис.104), где, в свою очередь,
.
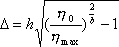Как видно из этих выражений, энергия цунами от макросейсмического источника в конечном счете зависит от длины разлома в очаге (другими словами - от магнитуды) и глубины очага землетрясения. Весьма интересно, как она согласуется с эмпирическими данными [Го, 1987]. Соответствующее сопоставление показано на рис.106а. Энергия цунами от макросейсмического источника определялась путем численного интегрирования (4.17), соответствующие зависимости E (M, h) показаны на рисунке сплошными линиями для значений h = 10, 20, 30, 40, 50, 60, и 70 км. Независимые данные используемой сводки показаны точками.
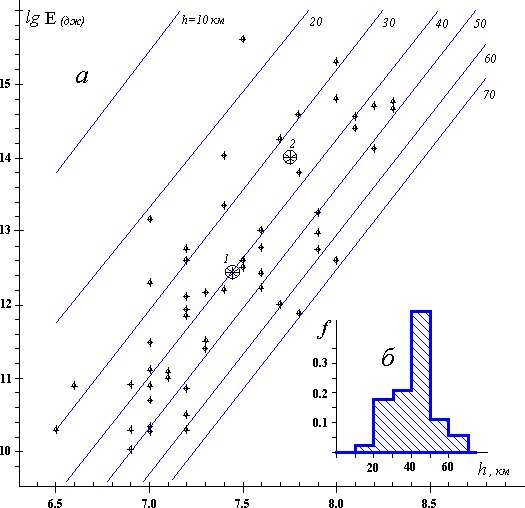
Рис.106а. Эмпирические данные о логарифмах энергии цунами в зависимости от магнитуды и аппроксимирующие их зависимости вида (4.17) для глубин очагов h = 10, 20, 30, 40, 50, 60 и 70 км. Точка (1) в виде звездочки соответствует средним значениям магнитуды землетрясения и энергии цунами по выборке [Го, 1987], точка (2) соответствует средним значениям этих величин для районов, примыкающим к островным дугам, по [Соловьев, 1972]
б. Гистограмма функции плотности распределения глубин очагов землетрясений при условии, что соотношение (4.17) справедливо.
Из рис.106а видно, что абсолютное большинство эмпирических точек концентрируется вблизи зависимостей вида (4.17) для глубин 20 Ј h <70 км (из указанного интервала выпадает только одна точка). Точка (1), соответствующая центру используемой здесь выборки попадает прямо на указанную зависимость, соответствующую глубине очага h = 40 км. Заметим, что зависимость вида (4.17) вычислялась без использования данных об энергии цунами, представленных на этом рисунке. Точка (2), соответствующая центру независимой выборки [Соловьев, 1972], находится между зависимостями вида (4.17) для глубин очага h = 30 и 40 км. Наконец, гипотетическая гистограмма функции плотности распределения глубин очагов землетрясений, построенная с помощью зависимостей вида (4.17) и изображенная на рис.106б, имеет максимум при глубине очага h = 40 км. Таким образом, и данные об энергии цунами неплохо согласуются с предположением о существовании линейной связи между логарифмом начальной высоты в источнике цунами и интенсивности сотрясений.
В результате проделанной работы появилось несколько возможностей для самой ранней прогностической оценки высоты цунами в источнике и на ближайших к нему берегах.
Первая из них состоит в использовании соотношения (4.8), формально вытекающего из соотношений (4.5) - (4.7) [Соловьев, 1972]. Высота цунами вычисляется как функция одной магнитуды. Ее можно интерпретировать как наиболее вероятную для островных дуг (при глубине очага землетрясения h = 40 км).
Вторая возможность существенно базируется на предположении, что заметные волны цунами возникают лишь в тех случаях, когда сила сотрясений в эпицентральной области больше или равна 9 баллам. Предельная глубина очага землетрясения, на которой достигается такая сила сотрясений является функцией его магнитуды и определяется соотношением (4.4) при Jt = 9 баллам. В качестве оценки высоты цунами в источнике можно воспользоваться величиной c0, определяемой соотношением (4.11) как малой полуоси эквивалентного по энергии источника цунами. Энергия, в свою очередь, оценивается из (4.8).
Наконец, третья возможность, в основе которой лежит предположение о непрерывной зависимости начального возвышения в источнике цунами от силы вызываемых землетрясением сотрясений, состоит в использовании соотношений (4.15) - (4.17). При M < 7.8 для оценки “цунамигенной” глубины очага необходимо пользоваться соотношением (4.4). Когда же M і 7.8 глубину следует принимать равной ее наивероятнейшему значению h = 40 км.
Все эти возможности еще предстоит проверить на доступном эмпирическом материале.
Предположение о связи начального возвышения в источнике цунами с силой сотрясений, вызываемых землетрясением влечет за собой необходимость изучения вопроса о возможной физической природе этой связи. Простейшее ее объяснение может состоять в том, что поле модуля остаточных смещений при землетрясении, в целом, имеет положительную корреляцию с его макросейсмическим эффектом. Такая связь, насколько нам известно, сейчас не установлена, хотя ее наличие достаточно очевидно. Было бы интересно выяснить этот вопрос, так как отсутствие тесной корреляции между макросейсмическим эффектом и полем модуля остаточных смещений будет ясно указывать на существование в природе пока не изученного исследователями механизма возбуждения цунами, который можно было бы назвать вибрационным.
Главный результат работы состоит в установлении того факта, что действующая Российская СПЦ, в принципе, в состоянии доставить предупреждение о цунами на основании сейсмологических наблюдений в большинство прикрываемых населенных пунктов заблаговременно при любом положении источника вблизи российских берегов. Вместе с тем, авторами обнаружены вполне возможные варианты взаимного расположения населенных пунктов и вероятных источников цунами, когда СПЦ будет не в состоянии доставить в некоторые пункты тревожное сообщение о цунами заблаговременно при существующих сейчас временных нормативах ее работы и принятом здесь достаточно условно минимальном времени эвакуации населения по тревоге. Учитывая, что вопросы точности вычисления времен пробега цунами, на основе которых сделан этот вывод, пока недостаточно изучены, этот вывод необходимо рассматривать как предварительный. Однако невозможность доставки в некоторые населенные пункты заблаговременных тревожных сообщений по объективным причинам (неблагоприятного географического расположения источника цунами по отношению к некоторым населенным пунктам) необходимо учитывать по крайней мере при последующем анализе действий СПЦ в тревожные периоды возникновения сильных подводных землетрясений.
Поскольку размеры и форма сейсмической зоны молчания определяются исключительно батиметрией примыкающей к населенному пункту акватории и минимальной временной дистанцией заблаговременности, большинство неблагоприятных случаев возможного незаблаговременного предупреждения о цунами может быть компактно описано заранее как область пересечения той или иной СЗМ и цунамигенной зоны. Отсюда вытекает возможность разработки индивидуальных условных алгоритмов работы СПЦ, используемых при условии, что эпицентр землетрясения попадает в конкретную такую область. Уже сейчас очевидно, что должны существовать специальные сейсмические станции, предназначенные, прежде всего, для прогнозирования цунами из указанных областей. Такие станции лучше всего устанавливать прямо в самих населенных пунктах, имеющих пересечения собственных СЗМ с цунамигенной зоной (таким образом минимизируется необходимая длительность регистрации землетрясения в наиболее неблагоприятных случаях). При регистрации землетрясения из области незаблаговременного предупреждения для пункта расположения станции, последняя должна перейти на индивидуальный регламент работы, позволяющей ее персоналу самостоятельно подавать тревогу цунами. Длительность ее работы в тревожном режиме (от начала регистрации и до выдачи в каналы связи тревожного сообщения) должна определяться эпицентральным расстоянием регистрируемого землетрясения, которое по данным главы 3 составляет от 0 до ~300 км, что соответствует длительности информативного участка записи менее 1 минуты (разность S - P Ј 30 секунд). Используя существующие методы автоматической обработки сейсмической записи, например, [Никифоров, Тихонов, Михайлова, 1989, Тихонов 1994], результаты, изложенные в главе 4 и современную вычислительную технику, можно, по-видимому, рассчитывать на то, что тревожное сообщение с такой станции будет поступать в каналы связи не позднее, чем через 2 минуты после начала такого землетрясения. Вопрос о том, сколько необходимо таких станций, нужно ли их устанавливать в каждом пункте, имеющем “непустую” область пересечения СЗМ с цунамигенной зоной, должен решаться индивидуально для каждого из рассмотренных в главе 3 регионов.
Размеры и форма гидрофизических зон молчания прикрываемых населенных пунктов в значительной степени зависят (помимо батиметрии примыкающей акватории и принятой минимальной временной дистанции заблаговременности) еще и от расположения относительно них станций измерения уровня океана. Размер ГЗМ конкретного населенного пункта всегда значительно больше размера соответствующей СЗМ, поэтому заблаговременные предупреждения о цунами ближайших к источнику населенных пунктов, выработанные по данным гидрофизических наблюдений, будут скорее исключением, чем правилом в наиболее сейсмичных и цунамиактивных регионах, примыкающих со стороны Тихого океана непосредственно к побережью Камчатки и Курильских островов. Для большей части прикрываемого побережья Берингова и Японского морей возможна такая расстановка уровенных станций, которая обеспечит заблаговременное предупреждение его о цунами по данным гидрофизических наблюдений при любом расположении источника в пределах цунамигенной зоны. При этом иногда будет возможно получить количественный прогноз ожидаемой высоты волны у тех или иных населенных пунктов по данным наблюдений уровенных станций. Определенные надежды на это основываются на результатах, изложенных в главе 5.
Хорошая, с точки зрения потребителя (то есть населения и хозяйства прибрежной полосы суши), работа любой СПЦ определяется не только качеством самой работы, каким бы путем мы его ни определяли (с помощью вероятностей ошибочных решений или социальной и экономической эффективности). Оно зависит, во-первых, от того насколько благоприятствует взаимное расположение вероятных источников и прикрываемых населенных пунктов получению ими заблаговременных предупреждений о цунами (географический фактор). Во-вторых, оно зависит, конечно от качества работы самой СПЦ и системы связи, ее обслуживающей (научно-технический фактор). Наконец, для того, чтобы достоверное и доставленное с максимальной оперативностью предупреждение о цунами действительно оказалось полезным, необходимо, чтобы население предупреждаемых пунктов и движимое имущество можно было с максимальной скоростью эвакуировать в безопасные места. Для этого необходимо не только благоприятное действие вышеназванных факторов, но и готовность населения и имущества к быстрой эвакуации, что требует определенных (и, возможно, не малых) затрат на подготовительные и защитные работы (культурный фактор). К таким работам относятся просветительская работа среди населения, определение и оборудование мест эвакуации населения с учетом реальных возможностей заблаговременного предупреждения о цунами конкретного населенного пункта, уточнение индивидуально для каждого населенного пункта минимального времени эвакуации, разработка методов защиты портов и правил стоянки судов вблизи берегов, подверженных опасности цунами, в зависимости от их маневренности и водоизмещения, строгое регламентирование застройки суши в непосредственной близости к береговой черте. На самых ранних этапах проектирования новых крупных хозяйственных близбереговых объектов - при выборе места под строительство - в числе прочих уже учитываемых неблагоприятных природных факторов, необходимо учитывать не только долговременную опасность цунами, но и реальные возможности действующей СПЦ обеспечить проектируемый объект заблаговременными прогнозами цунами.