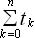 ; (3)
; (3)где: k - номер элементарного участка; n - число элементарных участков; tk - время движения на каждом элементарном участке.
Мореходство и морские науки
Морской форум 12 февраля 2008 г
Выбор типа и основных характеристик гребного винта во многом определяет экономические показатели судна. Для обычных транспортных судов основным режимом движения является полный ход. Именно на этот режим рассчитывают гребной винт. Но для многих судов характерны, по крайней мере, два существенно различных режима: полный ход и движение с малой скоростью, но большой тягой. Это, например, буксиры, траулеры, суда ледового плавания.
Наиболее распространенный тип судового движителя – гребной винт фиксированного шага. Он всегда рассчитывается на совершенно определенный режим, при отклонении от которого нарушается соответствие между винтом, корпусом и двигателем. В качестве альтернативных вариантов могут использоваться винты регулируемого шага, более сложные и дорогие, но позволяющие достигать соответствия с двигателем и корпусом. Для обоих типов винтов, кроме того, можно применять направляющие насадки, заметно увеличивающие тягу на малых скоростях, но неэффективные на полном ходу.
В начальной стадии проектирования необходимо выбрать оптимальный вариант движителя, по возможности избегая трудоемких и длительных расчетов используя приближенные методы.
Some aspects of propulsion complex designing for ships with a several regime of movement
S.V. Antonenko, M.V. Kitaev
The choice of the type and the basic characteristics of the screw propeller in many respects defines economic parameters of a vessel. For the transport vessels the normal regime of movement is the full speed. It is this regime for which the screw propeller is calculate. But for many vessels at least the two essential different regimes of movement are typical: a full speed regime and movement at slow speed, but with large tractive force. They are for example, tugs, trawlers, arctic navigation vessels, ice-breakers and so on.
The most widespread type of propeller - is the fixed pitch propeller. It is always calculate for absolutely certain regime, at a deviation from which the conformity between the screw, hull and engine breaks. As alternative variants variable-pitch propeller, can be used which are more complex and expensive, but allowing to attain conformity between the engine and the hull. Besides for both types of propellers the nozzles can be applied which noticeably increase tractive force at small speeds, but inefficient at full speed.
In an initial stage of design it is necessary to choose an optimum variant of propeller, as far as possible avoiding difficult calculations and using the approached methods.
Современные экономические условия характеризуются все более жесткой конкуренцией на международном рынке судостроения, что ставит перед проектантами и судовладельцами новые проблемы, к числу которых можно отнести:
- создание экономически выгодных судов, позволяющих получать наибольшую прибыль;
- ограниченность времени, требующегося для создания судна и ввода его в эксплуатацию;
- снижение затрат, связанных с созданием и эксплуатацией судна;
- повышение качества проектирования и постройки судна.
С точки зрения проектирования, конкурентоспособность вновь создаваемых судов в большой степени зависит от глубины проработки технического задания на проектирование и обоснованности принимаемых проектных решений. Экономические показатели судна во многом определяются выбором типа и основных характеристик судового движителя.
На судах морского и речного флота чрезвычайно широкое распространение в качестве основного движителя получили гребные винты благодаря своей простоте и высокой эффективности. Наиболее высокий кпд при максимальной простоте достигается у винтов фиксированного шага (ВФШ). Благодаря этим преимуществам ВФШ используются на большинстве транспортных судов. Однако для ВФШ существует один совершенно определенный расчетный режим работы, для которого и определены его характеристики и на котором обеспечивается наивысшая эффективность. На других режимах винт становится или «легким», или «тяжелым», он не может использовать полную мощность двигателя.
У транспортного судна основным режимом движения является полный ход. Отклонения от этого расчетного режима при эксплуатации (изменения скорости хода и сопротивления движению) вызываются множеством причин: влиянием ветра и волнения, обрастания и коррозии наружной обшивки, изменениями состояния нагрузки и др. Но такие отклонения от расчетного режима сравнительно невелики и не слишком сильно влияют на эффективность гребного винта.
В то же время имеется группа судов, для которых режим полного хода не является безусловно основным, но большое время занимает движение при значительно увеличенном сопротивлении. К ним относятся, например, траулеры, буксиры, суда ледового плавания. При проектировании движительного комплекса таких судов необходимо учитывать как режим полного хода, так и режим движения с малой скоростью, но с увеличенной тягой движителя (ход с тралом, буксировка другого судна, движение в сплошном льду). Если для такого судна проектируется ВФШ, то его характеристики (диаметр, шаговое и дисковое отношения) будут различными, в зависимости от того, на какой именно режим проектируется винт. Здесь возможны, по крайней мере, три варианта:
1) скоростной винт с максимальным шаговым отношением, но с ухудшенными тяговыми характеристиками;
2) тяговый винт с малым шаговым отношением, не позволяющий развивать высокую скорость;
3) компромиссный винт, не обеспечивающий полное использование мощности двигателя ни на полном, ни на малом ходу, но дающий удовлетворительные результаты на обоих,
резко различных режимах.
Для указанной группы судов могут быть рациональными другие варианты движительного комплекса, например, винты регулируемого шага (ВРШ). Их несомненное достоинство в том, что они позволяют обеспечить соответствие двигателю и его работу на номинальном режиме при любых условиях плавания за счет разворота лопастей, т.е. изменения шага. Но кпд ВРШ на расчетном режиме всегда меньше, чем у ВФШ, а при развороте лопастей он дополнительно уменьшается. Стоимость ВРШ с механизмом изменения шага во много раз больше, чем ВФШ.
Другая возможность повышения эффективности движительного комплекса связана с установкой направляющей насадки на винт (неподвижной или поворотной). Как известно, насадка позволяет значительно увеличить упор на малых скоростях, когда винт тяжело нагружен. Но на режиме полного хода она неэффективна. Кроме того, насадка также увеличивает стоимость движительного комплекса.
Таким образом, на судах, отличающихся наличием двух резко различных режимов хода, могут применяться, по крайней мере, четыре варианта движительного комплекса: винты фиксированного или регулируемого шага, в насадках и без них. Комплекс может включать один винт или два винта. Каждый из этих вариантов имеет свои достоинства и недостатки. Обоснованный выбор движительного комплекса для таких судов требует технико-экономического анализа. Этот анализ может производиться на основе детального рассмотрения процесса эксплуатации судна, например, с использованием имитационного моделирования. Такой подход позволяет учесть относительное время работы судна на различных режимах, удаленность районов эксплуатации и другие факторы, в том числе случайного характера.
В данной работе обсуждаются некоторые аспекты проблемы обоснования выбора движительного комплекса для судов, отличающихся наличием двух резко различных режимов хода. Предлагаются зависимости, которые могут быть использованы для компьютерного моделирования ходкости судов с различными типами движительного комплекса.
Проблема повышения экономичности судов всегда была очень актуальной и привлекала внимание как проектировщиков, так и судовладельцев. В последние годы, в связи со значительным ростом цен на топливо, требования к экономичности проектируемого судна значительно возросли. В настоящее время до 60 % (в зависимости от типа и назначения судна) текущих эксплуатационных затрат приходится на топливо. Поэтому решение проблемы экономии топлива напрямую связано с экономической эффективностью любого судна.
В общем случае, задачи подобного рода решаются по двум основным направлениям:
1) совершенствование энергетического оборудования судна (главных и вспомогательных двигателей, судовых устройств, систем и т.д.);
2) улучшение пропульсивных качеств судна (снижение сопротивления движению корпуса судна, повышение эффективности движителей, улучшение взаимодействия движителя
с корпусом и т.д.).
При этом как первый, так и второй путь чаще всего реализуются на этапе проектирования и постройки судна.
В данной работе рассматриваются вопросы, связанные со вторым направлением - повышением пропульсивных качеств судов.
Большое влияние на пропульсивные качества оказывает тип движительного комплекса. Выбор типа и основных характеристик движительного комплекса во многом определяет экономические показатели судна. На подавляющем большинстве судов в качестве основных движителей используются гребные винты, поэтому мы здесь не затрагиваем вопросы, связанные с проектированием других типов движителей: крыльчатых, водометных, а также движителей типа «Азипод». Будем ограничивать выбор типов движителей гребными винтами фиксированного или регулируемого шага, в направляющих насадках или без них.
Задача проектирования пропульсивного комплекса, в рамках оптимизационного проектирования судов, рассматривается как задача внутреннего проектирования, а именно - определение основных характеристик подсистемы судна, при удовлетворении требований технического задания и наилучших экономических показателях эффективности.
Выбор типа пропульсивного комплекса для проектируемого судна относится к числу принципиальных вопросов проектирования судов. В математическом смысле задачи такого рода относятся к задачам дискретной оптимизации, которые могут быть решены либо в рамках оптимизации основных параметров (основных элементов и характеристик) судна, либо в качестве отдельной задачи.
В задаче оптимизации основных параметров судна оптимизируемые параметры подразделяются на дискретные nj (j = 1..m) и непрерывные xi (i = 1..k). Тогда возможные решения задачи можно определить как комбинацию значений векторов (X, N):
X = (x1,…,xk);
N = (n1,…,nm); (1)
Тип пропульсивного комплекса как дискретный параметр входит в число компонентов вектора N.
Следовательно, оптимизация основных параметров судна сводится к нахождению экстремума целевой функции F(X, N) при (X, N) Î R, где R – множество допустимых решений:
F(X, N) ® extr. (2)
Функция F(X, N) представляет собой экономический критерий, зависящий от целей и задач моделирования. Таким образом, каждый вариант решения (альтернатива) будет иметь конкретное экономическое обоснование.
Область допустимых значений векторов определяется ограничениями задачи, которые могут иметь различный состав в зависимости от назначения судна, условий постройки и эксплуатации. Для большей достоверности результатов необходимо учитывать связь различных вариантов решений с внешними факторами.
При решении задач подобного рода часто используют методы принятия решений в условиях неопределенности, т.к. результат принятого решения зависит не только от предпочтений заказчика (проектанта) и фиксированных факторов, но и от неопределенных факторов, не контролируемых и неизвестных в момент принятия решения. Если имеется возможность получить вероятностное описание исходных данных, могут быть использованы стохастические модели.
Кроме того, необходимо учитывать принцип множественности моделей – создаваемая модель должна отражать в первую очередь те свойства системы, которые в большей степени оказывают влияние на выбранные показатели эффективности. Соответственно при использовании конкретной модели познаются лишь некоторые стороны вопроса. Для получения более полной и подробной информации необходимо создать целый ряд моделей, позволяющих с разных сторон и с разной степенью точности исследовать поставленную проблему.
Конкретных рекомендаций подобного рода не существует, т.к. многое определяется целью и задачами моделирования и зависит только от требований заказчика и проектанта.
Рассмотрим один из возможных вариантов решения проблемы выбора оптимального пропульсивного комплекса судна, для которого характерны два резко различных режима хода.
Под пропульсивным комплексом обычно понимают систему взаимодействующих компонентов: корпуса судна, главных двигателей, движителей определенного типа и устройства передачи мощности к ним, если последние имеются.
Для формулировки общей постановки задачи оптимизации пропульсивного комплекса судна примем обычные упрощения, которые позволят получить решение с помощью известных методов оптимизации, и некоторый критерий, по которому будет оцениваться качество полученного решения.
Главное упрощение рассматриваемой задачи заключается в том, что рейс судна разбивается на элементарные участки с относительно постоянными характеристиками: ветро-волновыми, ледовыми и др. Это позволяет рассматривать движение судна как равномерное на каждом из этих участков, причём время разгона и торможения судна не принимается во внимание.
Определение продолжительности рейса судна, таким образом, сводится к определению суммы векторов tk, характеризующих длительность прохождения каждого элементарного участка пути:
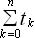 ; (3)
; (3)
где: k - номер элементарного участка; n - число элементарных участков; tk - время движения на каждом элементарном участке.
Оценку эффективности использования пропульсивного комплекса определенного типа можно оценивать по нескольким критериям для получения более полной информации о влиянии типа комплекса и его характеристик на различные показатели.
Критериями оценки рассматриваемых альтернатив Fi могут быть прямые эксплуатационные расходы, себестоимость выполняемых работ, прибыль и т.д.
Попутно можно рассматривать задачу выбора оптимальной скорости хода судна по условию минимального расхода топлива. Задача выбора оптимальной с экономической точки зрения скорости хода является едва ли не самой главной. Она может решаться не только на стадии проектирования судна, но и во время эксплуатации, когда пропульсивный комплекс уже существует.
Экономическая сущность задачи может не исчерпываться только значением определенного критерия F. Дополнительные условия задачи формулируются в виде ограничений на значения компонент вектора времени tk. Существуют также ограничения, имеющие чисто технический смысл: это величины максимальной и минимальной скоростей судна. Очевидно, что эти величины будут зависеть от условий плавания. Это означает, что в качестве исходных данных задачи должны быть определены два вектора tkmin и tkmax, ограничивающие значения соответствующих компонент вектора tk. Таким образом, задача оптимизации режима движения судна будет в общем случае сформулирована в виде:
F(tk) ® min; (4)
tkmin < tk < tkmax
Решение данной задачи требует наличия математической модели, которая учитывает технические характеристики судна, работу пропульсивного комплекса, условия плавания (внешние воздействия на судно: ветер, волнение, ледовая обстановка) и др. В модель необходимо включить блоки, позволяющие выполнять расчеты:
1) сопротивления корпуса судна;
2) гидродинамических характеристик гребных винтов различных типов;
3) расхода топлива двигателей.
Это позволит без особых сложностей выполнить интеграцию различных моделей в единую комплексную модель, которая обеспечит полноту и достоверность результатов моделирования, а также позволит разработать соответствующую методику, дающую возможность на этапе предварительного проектирования достаточно полно и обоснованно принимать решения, относящиеся к выбору типа пропульсивного комплекса.
Рассматривая вопрос выбора оптимального пропульсивного комплекса, еще раз отметим, что даже при наличии математической модели проектант не всегда выполняет комплексную сравнительную оценку эффективности различных вариантов пропульсивного комплекса, а ограничивается рассмотрением одного – двух вариантов, что не позволяет сделать полные и достаточно обоснованные выводы об эффективности принятого решения.
На начальной стадии проектирования необходимо выбрать оптимальный вариант движителя, по возможности избегая трудоемких и длительных расчетов и используя относительно простые методы. На этой стадии еще не проводятся и модельные испытания. При практических расчетах широко используются различные графические зависимости, основанные на результатах модельных испытаний серий судов определенного типа для определения сопротивления движению судна и характеристик движительного комплекса. Для поиска оптимального варианта с использованием математических моделей эти зависимости необходимо преобразовать к удобному для реализации на компьютере виду - или в форме полиномов, или путем интерполяции табличных значений (что менее удобно при использовании).
В данной работе основное внимание уделяется выбору типа движителя, тогда как главный двигатель считается заданным. При этом имеется в виду возможность оптимизации основных характеристик судна по условиям ходкости. Вопросы ходкости и мореходности являются неотъемлемой частью как при проектировании, так и при оценке мореходных качеств уже существующего судна.
Как известно, целью проектировочного расчета является выбор элементов гребного винта, обеспечивающих достижение наивысших пропульсивных качеств движительного комплекса и соответствие характеристик винта и механической установки. Для практической реализации такой задачи, помимо параметров, характеризующих геометрию корпуса судна, и характеристик энергетической установки, должна быть определена зависимость сопротивления судна от скорости хода. Эта зависимость неоднозначна и определяется состоянием нагрузки судна, режимом и условиями эксплуатации, что приводит к изменению достижимой скорости хода судна при использовании полной мощности энергетической установки. Установление указанной зависимости актуально для всех без исключения судов.
Авторами выполнена работа по переводу некоторых графических зависимостей для определения сопротивления судна и характеристик пропульсивного комплекса в форму, удобную для создания математических моделей. Получены полиномиальные зависимости для определения остаточного сопротивления малых и среднетоннажных промысловых судов, основанные на результатах серийных испытаний моделей судов, выполненных В.А. Ерошиным в 1975 ¸ 1980 гг. [1, 2, 3], а также зависимости для определения кривых действия гребных винтов регулируемого шага и винтов в насадках. Полиномы для расчета винтов фиксированного шага (без насадок) имеются в литературе [6, 7, 10].
Полученные полиномиальные зависимости позволяют выполнять сопоставительные расчеты ходкости в целях выбора оптимального типа движительного комплекса и характеристик гребных винтов судов с несколькими режимами движения с учетом экономических показателей эффективности.
Согласно методике расчета остаточного сопротивления промысловых судов по диаграммам В.А. Ерошина [6], безразмерный коэффициент остаточного сопротивления определяется по формуле:
CR[j i, (Lpp/B)i, (B/T)i, b
i, Xci, Fr] =
CR[j i, (Lpp/B)0, (B/T)0, b
0, Xc0, Fr]
´ CR[j 0, (Lpp/B)i, (B/T)0,
b 0,Xc0, Fr]
´ CR[j 0, (Lpp/B)0,
(B/T)i, b 0, Xc0, Fr]
´ CR[j 0,
(Lpp/B)0, (B/T)0, b i, Xc0, Fr]
´ CR[j
0, (Lpp/B)0,(B/T)0, b 0, Xci, Fr]
´ CR-4[j
0, (Lpp/B)0, (B/T)0, b 0, Xc0, Fr], (5)
где CR - коэффициент остаточного сопротивления; j - призматический коэффициент продольной остроты; Lpp/B - отношение длины между перпендикулярами к осадке; В/Т – отношение ширины судна к его осадке; b - коэффициент полноты площади мидель-шпангоута; Xc – относительное положение центра величины по длине судна; Fr – число Фруда; индекс «i» относится к геометрическим параметрам корпуса судна, для которого выполняется расчет; «0» - к геометрическим параметрам корпуса базовой модели, которые для среднетоннажных судов приняты: Lpp/B = 4,25; B/T = 2,6; j pp = 0,6; b = 0,833; XC= -0,01. Для малых промысловых судов базовая форма обводов имеет отношение Lpp/B = 3,0; остальные значения параметров формы корпуса те же, что и для среднетоннажных судов. Такая форма представления результатов позволяет выявить характер влияния каждого геометрического параметра на величину CR.
Остаточное сопротивление определяется по формуле:
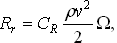 (6)
(6)
где: CR - коэффициент остаточного сопротивления; ρ – плотность жидкости; v – скорость судна; Ω – площадь смоченной поверхности.
По предварительной оценке, при внесении определенных поправок эта методика применима и при расчете сопротивления многих буксиров.
Диапазоны изменения основных характеристик для среднетоннажных промысловых судов:
0,55Ј jрр
Ј 0,7;
3,5 Ј Lрр/B Ј 5,0;
2,3 Ј B/T
Ј 3,2;
0,65 Ј b Ј 0,92;
-0,03 Ј
XCЈ 0,01;
0,21 Ј Fr Ј 0,37.
Зависимость коэффициента остаточного сопротивления от характеристик формы корпуса судна CR = f(j i, (Lpp/B)i, (B/T)i, b i, Xci, ai) можно представить в следующем виде:
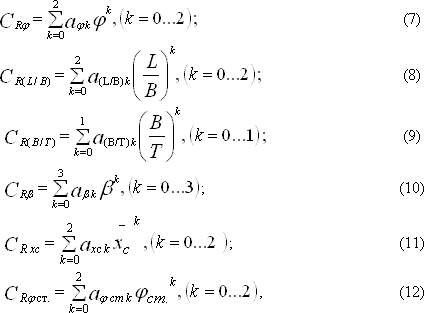
где a – коэффициенты, являющиеся функцией от числа Фруда a = f(Fr), определяются по следующим зависимостям:
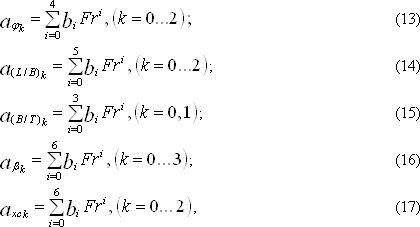
где bi – числовые коэффициенты, значения которых приведены в табл. 1 – 5.
Большое количество значащих цифр после запятой определяется малыми разностями близких величин. Все коэффициенты сопротивления следует умножать на 0,001.
Для малых промысловых судов ограничения на диапазоны изменения основных характеристик формы корпуса определяются следующими величинами:
0,5
Ј jрр Ј 0,72;
2,5 Ј Lрр/B
Ј 3,5;
2,6 Ј B/T Ј 4,0;
0,75 Ј b
Ј 0,92;
-0,05 Ј XCЈ 0,01;
0,10 Ј Fr
Ј 0,50.
Таблица 1
Коэффициенты аппроксимации по коэффициенту j
| bi | aj 0 | aj 1 | aj 2 |
| b0 | - 2848,286 | 8395,277 | - 5846,643 |
| b1 | 44864,682 | - 135898,783 | 98317,491 |
| b2 | - 258963,234 | 804054,532 | - 600576,571 |
| b3 | 648850,141 | - 2060721,261 | 1582055,311 |
| b4 | -592292,381 | 1920038,923 | -1507914,644 |
Таблица 2
Коэффициенты аппроксимации по параметру L/B
| bi | a(L/B) 0 | a(L/B) 1 | a(L/B) 2 |
| b0 | - 538,779 | 277,879 | - 34,292 |
| b1 | 10719,707 | - 5497,266 | 692,400 |
| b2 | - 85003,352 | 43277,316 | - 5543,417 |
| b3 | 335832,592 | - 169210,601 | 21941,185 |
| b4 | - 661648,338 | 329003,293 | - 42964,657 |
| b5 | 520808,311 | -254480,898 | 33277,585 |
Таблица 3
Коэффициенты аппроксимации по параметру В/Т
|
bi |
a(B/T) 0 |
a(B/T) 1 |
| b0 | - 33,088 | 2,629 |
| b1 | 383,148 | - 30,519 |
| b2 | - 1448,286 | 114,490 |
| b3 | 1935,343 | -150,070 |
Таблица 4
Коэффициенты аппроксимации по коэффициенту b
| bi | ab 0 | ab 1 | ab 2 | ab 3 |
| b0 | 212399,694 | - 817602,385 | 1030444,942 | - 428558,891 |
| b1 | - 4599691,313 | 17672030,199 | - 22225753,402 | 9221265,606 |
| b2 | 40998073,448 | - 157152809,133 | 197142343,091 | - 81551295,474 |
| b3 | 192542334,764 | 736042405,377 | - 920517081,717 | 379442777,373 |
| b4 | 502699000,801 | - 1915614401,935 | 2387152713,162 | - 979912265,23 |
| b5 | - 692247640,09 | 2628372727,229 | - 3261894041,727 | 1332565018,751 |
| b6 | 393068289,729 | -1486353487,57 | 1836050765,07 | -745980894,273 |
Таблица 5
Коэффициенты аппроксимации по параметру Хс
| bi | axc 0 | axc 1 | axc 2 |
| b0 | - 1420,317 | - 8061,527 | 1104712,927 |
| b1 | 30875,143 | 203573,852 | - 24011720,712 |
| b2 | - 276980,230 | - 2115389,124 | 215033024,647 |
| b3 | 1312294,821 | 11559898,522 | - 1015738129,667 |
| b4 | - 3460992,975 | - 35032354,554 | 2670049602,950 |
| b5 | 4816962,527 | 55870212,103 | - 3704677435,556 |
| b6 | -2762310,755 | -36649254,291 | 2120238291,352 |
Зависимость коэффициента остаточного сопротивления от характеристик формы корпуса судна для малых промысловых судов выражается формулами:
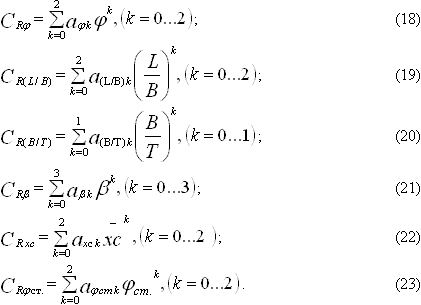
Значения вспомогательных коэффициентов, зависящих от числа Фруда, определяются следующими выражениями:
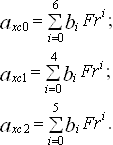 (24)
(24)
Таблица 6
Коэффициенты аппроксимации по параметру Хс
| bi |
Fr > 0,36 |
Fr £ 0,36 |
|||
|
axc 0 |
axc 1 |
axc 2 |
axc 1 |
axc 2 |
|
| b0 | - 149,150 | - 108444,660 | 4107560,850 | - 1926,786 | - 14082,769 |
| b1 | 3755,163 | 1039331,340 | - 50896672,210 | 37253,583 | 278399,175 |
| b2 | - 37521,547 | - 3736072,990 | 250800648,470 | - 261004,047 | - 1983733,216 |
| b3 | 192909,885 | 5970601,090 | - 615086192,530 | 764941,638 | 5690610,108 |
| b4 | - 539668,919 | -3578391,340 | 751661664,930 | -795835,641 | - 5090701,414 |
| b5 | 779539,948 |
-- |
-366508313,260 |
-- |
-1501084,691 |
| b6 | -451169,673 | -- | -- | -- | -- |
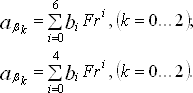 (25)
(25)
Таблица 7
Коэффициенты аппроксимации по коэффициенту b
| ab i |
Fr(i) > 0,3 |
Fr(i) £ 0,3 |
||||
|
ab 0 |
ab 1 |
ab 2 |
ab 0 |
ab 1 |
ab 2 |
|
| b0 | 2028746,357 | - 5379566,490 | 3483945,471 | - 1452,895 | 3423,552 | - 2019,264 |
| b1 | - 31295473,447 | 82927594,420 | - 53683944,824 | 28489,442 | - 67254,675 | 39779,237 |
|
b2 |
200180680,498 | - 530055734,480 | 342981400,197 | - 204319,821 | 483461,961 | - 286521,598 |
| b3 | - 679550527,578 | 1797998281,940 | - 1162847941,291 | 644084,999 | - 1528704,674 | 908338,701 |
| b4 | 1291121937,922 | - 3413444062,180 | 2206435629,479 | -748757,124 | 1783412,793 | -1062541,539 |
| b5 | - 1301644106,565 | 3438513806,980 | - 2221337528,632 | -- | -- | -- |
| b6 | 543937175,899 | -1435752065,450 | 926938479,035 | -- | -- | -- |
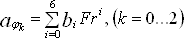 ; (26)
; (26)
Таблица 8
Коэффициенты аппроксимации
|
aj 0 |
aj 1 |
aj 2 |
|
| b0 | - 3870,052 | 15465,304 | - 15298,822 |
| b1 | 88688,529 | - 354287,844 | 351354,837 |
| b2 | - 808276,81 | 3222917,060 | - 3201813,247 |
| b3 | 3739769,023 | - 14865888,210 | 14793395,55 |
| b4 | - 9282797,763 | 36722032,624 | - 36595287,807 |
| b5 | 11855353,401 | - 46509676,942 | 46339304,150 |
| b6 | -6149098,152 | 23828947,902 | -23673069,284 |
Для чисел Фруда Fr > 0,32 зависимости коэффициентов полиномов представлены в виде рациональных многочленов (27), числовые коэффициенты которых приведены в табл. 9.
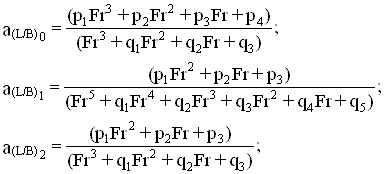 (27)
(27)
Таблица 9
Коэффициенты аппроксимации по параметру L/B
| a(L/B) 0 | a(L/B) 1 | a(L/B) 2 | |
| p1 | -1468 | 795,6 | -5448 |
| p2 | - 465,6 | 118,5 | 2919 |
| p3 | - 1948 | - 238,7 | - 166,2 |
| p4 | 1418 | -- | -- |
| q1 | 1164 | - 59,2 | 3955 |
| q2 | - 1041 | - 732,9 | - 3670 |
| q3 | 235,4 | 1316 | 858,3 |
| q4 | -- | - 722,8 | -- |
| q5 | -- | 128,5 | -- |
Для чисел Фруда Fr £ 0,32 применяется полиномиальная зависимость:
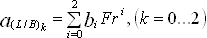 . (28)
. (28)
Таблица 10
Коэффициенты аппроксимации по параметру L/B
| a(L/B) 0 | a(L/B) 1 | a(L/B) 2 | |
| b0 | 3,717 | 2,5361 | - 0,717 |
| b1 | 36,896 | - 55,632 | 10,358 |
| b2 | 108,765 | 22,958 | -7,329 |
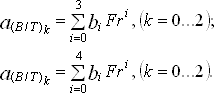 (29)
(29)
Таблица 11
Коэффициенты аппроксимации по параметру В/Т
| bi |
Fr > 0,38 |
Fr £ 0,38 |
||||
| a(B/T) 0 | a(B/T) 1 | a(B/T) 2 | a(B/T) 0 | a(B/T) 1 | a(B/T) 2 | |
| b0 | 6404,60 | - 2096,04 | 118,50 | 100,50 | - 27,571 | 2,2985 |
| b1 | - 43443 | 13944,65 | - 740,5 | - 1811 | 520,35 | - 43,642 |
| b2 | 96986 | - 30464,7 | 1488,2 | 12546 | - 3820,6 | 332,87 |
| b3 | -70713 | 21739,58 | -947,45 | - 37704 | 12097 | - 1090,9 |
| b4 | -- | -- | -- | 41384 | -13721 | 1268,7 |
Широкое распространение в мировой практике получили серии гребных винтов, разработанные и испытанные в Вагенингенском опытовом бассейне (Нидерланды; серии «В» или серии Трооста). Основным достоинством гребных винтов этих серий является широкая вариация геометрических элементов и надежность полученных данных по гидродинамическим характеристикам, а также наличие сквозной (по шаговому и дисковому отношениям, числу лопастей) аналитической аппроксимации кривых действия степенными функциями [6, 7, 9, 10].
Существует достаточно большое количество работ подобного вида. Первые работы были направлены на автоматизацию процесса вычисления гидродинамических характеристик гребных винтов. Актуальность данной проблемы стала возрастать с активным внедрением компьютерной техники в процесс проектирования судов.
Для расчета гидродинамических характеристик ВФШ использовались универсальные полиномы вида:
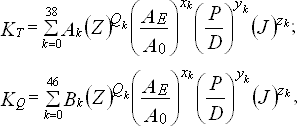 (30)
(30)
где: 2 £ Z £ 7;
0,4 £ Ae/A0 £
1,05;
0,5 £ P/D £ 1,4;
0 £ J £ 1,5.
По винтам в направляющих насадках и винтам регулируемого шага такие аппроксимации в известной нам литературе отсутствуют.
Авторами выполнена работа по аппроксимации некоторых графических зависимостей для определения гидродинамических характеристик винтов фиксированного шага в направляющих насадках и винтов регулируемого шага в насадках и без них. Результаты работы представлены ниже.
ВФШ в направляющих насадках представлены группой винтов, имеющих следующие характеристики: Z = 4; Ae/Ao = 0,35; 0,58; 0,75; 1,0; P/D = 0,7 ¸ 1,5, относительное удлинение направляющей насадки l/D = 0,6 [4, 5].
Зависимость коэффициента упора от относительной поступи представлена следующим выражением:
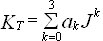 , (31)
, (31)
где коэффициенты ak являются функцией от шагового отношения и для значений дискового отношения Ae/Ao = 0,35 и 0,58 записываются в виде:
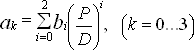 (32)
(32)
где: bi – числовые коэффициенты, приведенные в табл.13 – 14.
Таблица 13
Значения коэффициентов bi для дискового отношения Ae/Ao = 0,35
| bi | a0 | a1 | a2 | a3 |
| b0 | - 0,1858 | - 0,0979 | - 0,0577 | - 0,0364 |
| b1 | 0,7293 | - 0,4078 | - 0,1616 | 0,1145 |
| b2 | -0,0830 | 0,0209 | 0,2747 | -0,1341 |
Таблица 14
Значения коэффициентов bi для дискового отношения Ae/Ao = 0,58
| bi | a0 | a1 | a2 | a3 |
| b0 | - 0,2343 | 0,3969 | - 1,2095 | 0,7879 |
| b1 | 0,7322 | 1,2875 | 1,9512 | - 1,3825 |
| b2 | -0,0308 | 0,3918 | -0,7315 | 0,564 |
Для значений дискового отношения Ae/Ao = 0,75; 1,0 коэффициент упора определяется по формуле (31), а коэффициенты полинома ak определяются по следующим зависимостям:
Для Ae/Ao = 0,75
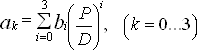 (33)
(33)
Таблица 15
Значения коэффициентов bi для дискового отношения Ae/Ao =0,75
| bi | a0 | a1 | a2 | a3 |
| b0 | - 0,2534 | 2,3064 | - 6,2263 | 4,4665 |
| b1 | 0,7255 | - 6,9977 | 16,868 | - 12,224 |
| b2 | 0,0083 | 5,7473 | - 14,706 | 10,656 |
| b3 | -- | -1,6245 | 4,2036 | -3,0183 |
Для Ae/Ao = 1,0
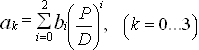 (34)
(34)
Таблица 16
Значения коэффициентов bi для дискового отношения Ae/Ao = 1,0
| bi | a0 | a1 | a2 | a3 |
| b0 | - 0,2484 | 0,1571 | 0,0816 | - 0,7668 |
| b1 | 0,727 | - 1,0043 | - 0,1285 | 1,2822 |
| b2 | 0,01 | 0,3174 | 0,0477 | -0,5247 |
Зависимость коэффициента момента от относительной поступи для винтов рассматриваемого типа определяется следующим выражением:
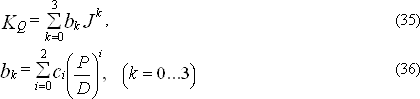
Таблица 17
Значения коэффициентов сi для дискового отношения Ae/Ao = 0,35
| ci | b0 | b1 | b2 | b3 |
| c0 | - 0,0916 | - 0,0544 | 0,2973 | - 0,4136 |
| c1 | 0,2322 | 0,0697 | - 0,8942 | 0,5019 |
| c2 | 0,2387 | -0,1549 | 0,5802 | -0,2814 |
Для Ae/Ao = 0,58 и Ae/Ao = 0,75 значения коэффициентов bk определяются как:
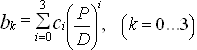 (37)
(37)
Таблица 18
Значения коэффициентов сi для дискового отношения Ae/Ao = 0,58
| ci | b0 | b1 | b2 | b3 |
| c0 | - 0,295 | 2,1899 | - 5,2468 | 3,9616 |
| c1 | 0,812 | - 6,4672 | 14,73 | - 11,56 |
| c2 | - 0,3476 | 5,9097 | - 13,471 | 10,324 |
| c3 | 0,2359 | -1,8452 | 4,0614 | -3,0059 |
Таблица 19
Значения коэффициентов сi для дискового отношения Ae/Ao = 0,75
| ci | b0 | b1 | b2 | b3 |
| c0 | - 0,2131 | 1,6746 | - 3,004 | 1,8457 |
| c1 | 0,5718 | - 5,3574 | 9,0353 | - 5,8231 |
| c2 | - 0,1744 | 5,2799 | - 9,0739 | 5,4391 |
| c3 | 0,2354 | -1,7513 | 2,9527 | -1,6582 |
Для Ae/Ao = 1,0 коэффициенты bk определяются по формуле:
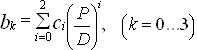 (38)
(38)
Таблица 20
Значения коэффициентов сi для дискового отношения Ae/Ao = 1,0
| ci | b0 | b1 | b2 | b3 |
| c0 | 0,0274 | 0,0027 | 0,1436 | - 0,3028 |
| c1 | - 0,1363 | - 0,1758 | - 0,3433 | 0,2383 |
| c2 | 0,5639 | 0,0212 | 0,0468 | -0,0594 |
Для получения истинных значений коэффициента момента необходимо значения, полученные по формуле (35), разделить на 10.
Для винтов регулируемого шага в направляющей насадке и без нее приведем аналитические зависимости для одного значения дискового отношения.
ВРШ без направляющей насадки имеет следующие характеристики: Z = 4; Ae/A0 = 0,48; конструктивное шаговое отношение P/Dк = 0,7.
Коэффициент упора определяется по следующей зависимости:
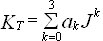 ; (39)
; (39)
Значения коэффициентов ak определяем по формуле:
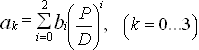 (40)
(40)
Таблица 21
Значения коэффициентов bi для ВРШ Ae/Ao = 0,48; P/Dk = 0,7.
| bi | a0 | a1 | a2 | a3 |
| b0 | - 0,0452 | - 0,1549 | - 0,285 | 0,0474 |
| b1 | 0,4437 | 0,0222 | - 0,5569 | 0,5744 |
| b2 | 0,039 | -0,0236 | 0,4283 | -0,4411 |
Коэффициент момента для рассматриваемого ВРШ определяется как
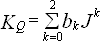 . (41)
. (41)
Значения коэффициентов bk определяем по формуле:
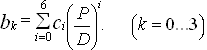 (42)
(42)
Таблица 23
Значения коэффициентов сi для ВРШ Ae/Ao = 0,48; P/Dk = 0,7.
| ci | b0 | b1 | b2 |
| c0 | 0,0016 | 0,0268 | - 0,0182 |
| c1 | 0,0696 | - 0,4384 | 0,246 |
| c2 | - 0,3538 | 2,7955 | - 2,1087 |
| c3 | 0,8136 | - 7,7526 | 6,1996 |
| c4 | - 0,6218 | 10,054 | - 8,326 |
| c5 | 0,1696 | - 6,2635 | 5,3061 |
| c6 | -- | 1,5176 | -1,3048 |
Коэффициент упора для ВРШ в направляющей насадке, имеющего следующие характеристики: Z = 4; Ae/A0 = 0,61; P/Dk = 0,9; l/D = 0,55, можно определить по формуле:
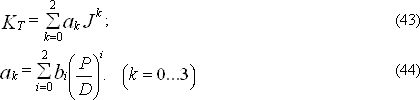
Таблица 22
Значения коэффициентов bi для ВРШ в направляющей насадке Ae/Ao = 0,61; P/Dk = 0,9.
| bi | a0 | a1 | a2 |
| b0 | 0,0751 | - 0,1339 | 0,0039 |
| b1 | 0,0994 | - 0,4862 | - 0,0137 |
| b2 | 0,3338 | 0,0565 | 0,0112 |
Коэффициент момента:
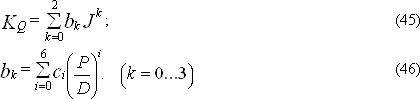
Таблица 24
Значения коэффициентов сi для ВРШ в направляющей насадкеAe/Ao = 0,61; P/Dk = 0,9.
| ci | b0 | b1 | b2 |
| c0 | - 0,1199 | 0,7183 | - 0,9313 |
| c1 | 0,9531 | - 3,0407 | 3,0297 |
| c2 | - 1,1275 | 3,8413 | - 4,141 |
| c3 | 0,7176 | -1,4951 | 1,6098 |
Для изучения влияния типа движительного комплекса на ходовые и пропульсивные качества судна составлен ряд программных модулей, позволяющих выполнять сопоставительные расчеты ходкости для заданного варианта судна, имеющего определенные главные размерения и коэффициенты полноты, а также выполнять оптимизационные расчеты по условию минимума сопротивления движению при сохранении постоянного водоизмещения и удельной грузовместимости.
В качестве примера на рис.1 приведены результаты расчета, выполненного для судна, имеющего следующие основные характеристики: L = 44,8 м; B = 13,8 м; T = 4,4 м; d = 0,48; b = 0,8; Zp = 1, Nгд = 2000 кВт, n = 176 об/мин. При выполнении вычислений предполагалось, что главные размерения судна остаются постоянными, а изменяется только тип движительного комплекса и его геометрические характеристики (геометрические характеристики винтов приведены в таблице 25). Для ВРШ указаны значения конструктивного шагового отношения.
Геометрические характеристики, приведенные в таблице 25, определялись с помощью программного модуля, позволяющего выполнять проектные расчеты и подбирать оптимальный гребной винт, спроектированный на определенный режим движения. На каждом графике имеются восемь кривых, показывающих зависимости: а) мощности Ne (кВт), б) упора Р (кН), в) кпд и г) частоты вращения гребного винта n (об/с) от скорости движения судна. Такое изображение результатов расчетов позволяет более наглядно сопоставить эффективность гребных винтов того или иного типа в зависимости от режима эксплуатации судна.
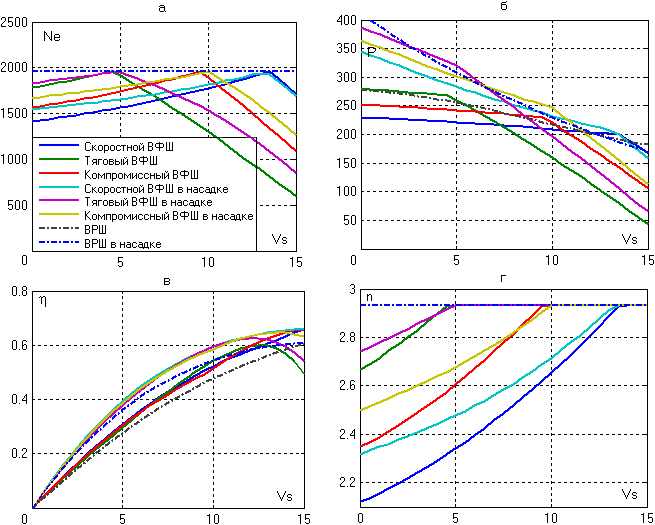
Рис.1. Зависимость: а. - мощности Ne (кВт), б. – упора винта Р (кН), в. - кпд, г. - оборотов двигателя n (об/с) от скорости движения судна:
Таблица 25
Геометрические характеристики гребных винтов
| Основные характеристики | D, м. | P/D | Ae/Ao |
| ВФШ (скоростной винт) | 3,3 | 0,95 | 0,62 |
| ВФШ (тяговый винт) | 3,3 | 0,73 | 0,76 |
| ВФШ (компромиссный винт) | 3,3 | 0,84 | 0,69 |
| ВФШ (скоростной винт в насадке) | 3,2 | 0,16 | 0,64 |
| ВФШ (тяговый винт в насадке) | 3,3 | 0,92 | 0,66 |
| ВФШ (компромиссный винт в насадке) | 3,25 | 1,00 | 0,65 |
| ВРШ | 3,3 | 0,92 | 0,61 |
| ВРШ в насадке | 3,26 | 0,93 | 0,61 |
D – диаметр гребного винта; P/D – шаговое отношение; Ae/Ao – дисковое отношение.
Выбор движительного комплекса для судов, обладающих несколькими, сильно отличающимися режимами движения, является нетривиальной задачей. Имеющиеся альтернативы обладают своими преимуществами и недостатками. Для принятия обоснованного проектного решения о выборе типа пропульсивного комплекса судна необходимо более строго подходить к вопросам оценки возможных вариантов решения.
Для обеспечения возможности компьютерного моделирования предлагается использовать аналитические зависимости, аппроксимирующие графики сопротивления судов соответствующих типов и кривые действия гребных винтов.
Использование указанных зависимостей для предварительного выбора типа движительного комплекса малого судна (типа буксира) показывает (см. рис. 1), что ВРШ в насадке позволяет при использовании полной мощности на любом режиме получать высокие тяговые характеристики (кривые б), в отдельных случаях лишь ненамного уступая другим вариантам движителей, для которых соответствующий режим хода является расчетным.
Полученные результаты сравнивались с «ручными» расчетами по диаграммам. Погрешности расчетов с помощью аппроксимационных полиномов оказались незначительными. Среднеквадратические погрешности аппроксимации не превышали 5%, а в большинстве случаев составляли 1–3 %.
Для более точной оценки эффективности движительного комплекса с учетом всей совокупности режимов эксплуатации целесообразно использовать методы имитационного моделирования, учитывая при этом стохастические и динамические факторы, влияющие на работу судна при эксплуатации.
В настоящее время ведется работа по созданию такой имитационной модели для буксирного судна. При построении модели предполагается использовать методы теории массового обслуживания. Разработанные программные модули могут внедряться в математические модели функционирования судов других типов.
Список литературы