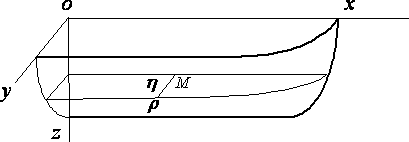
XI. The Wave-Resistance of a Ship.
By J. H. Michell.
[*] (Russian)
THE object of this paper is to give a general solution of the problem of the waves produced by a ship of given form moving with uniform velocity in an inviscid liquid, and to determine the consequent wave–resistance to the motion of the ship. The only assumption made as to the form of the ship is that the inclination of the tangent plane at any point of its surface to the vertical median plane is small. This condition is not satisfied near the bottom of the middle body of a modern ship, but it seems probable that this will not much affect either the waves produced or the resistance, for the waves arise rather from the parts at the bow and stern at which the tangent to the surface is inclined to the direction of the ship's motion, than from the approximately cylindrical middle body. The neglect of friction is probably of little consequence. The eddying water close to the side will no doubt slightly alter the virtual shape of the ship, but the change in the inclination of the virtual tangent plane, on which the wave–making depends, will, almost certainly, be very small. Further, the effect of viscosity in destroying the waves produced by the bow will modify to some extent the interaction of bow and stern waves; but, seeing that it is the waves of length comparable with that of the ship which chiefly give rise to the resistance, the effect must be small. The conclusion is, therefore, that the course followed by W. Froude, of considering frictional resistance and wave–resistance separately and adding the two, will probably give a close approximation to the truth.
A summary of the experimental work on this question, as well as a sketch of (he theoretical work of Russell, Rankine, and the two Froudes, is given in White's interesting 'Manual of Naval Architecture' (1894), chap. xi. Recent mathematics on the subject has been devoted chiefly to explaining, in a general way, the interesting wave–patterns observed, but exception must be made of the papers of Sir W. Thomson (Lord Kelvin), Phil.Mag. (1886–7), in which the critical speed of a canal boat, examined experimentally long before by Russell, was mathematically discussed. Reference may be made to Lamb's 'Hydrodynamics' (1895), chap, ix., and to Sir W. Thomson's 'Popular Lectures on Navigation' (1891), p. 450, for the discussion of wave–patterns.
None of these writers has, however, considered the waves produced by an actual ship, and the present paper is intended to supply the necessary investigation. The formula obtained for the wave–disturbance is rather complex, but that for the resistance is much simpler, as the most complicated term in the former represents a local disturbance not leading to any resistance in an inviscid liquid. There will therefore be no difficulty to those who have the necessary apparatus in making comparisons with experiment. As to general results, for deep water the theory leads to a resistance which increases with the velocity, in an oscillating manner, to a maximum and then decreases to zero as the velocity is indefinitely increased. That the resistance is an oscillating function of the velocity has been experimentally found by Mr. W.Froude and his son [†] , to whom also we owe the general explanation in terms of the interference of bow and stern waves. But the ultimate vanishing of the resistance has not, so far as I know, been anticipated. From general considerations it is clear that, so far as the wave–form is concerned, the effect of increasing the velocity is the same as that of decreasing the acceleration of gravity, and, if gravity vanishes, there is no propagation of waves; but this is not quite the theorem to be obtained.
Fig. 1
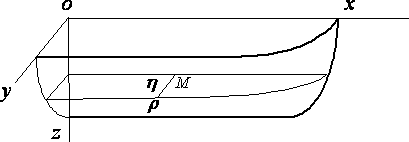
Take the vertical median plane of the ship as y = 0, and the surface of the undisturbed water as z = 0, the axis Ox being in the direction of motion of the ship and Oz vertically downwards. We may suppose the ship at rest and the water moving backwards with uniform velocity v apart from the wave–disturbance. The motion is assumed steady and the velocity potential written –vx + f. Since the inclination of the ship's surface to the plane y = 0 is everywhere small, f will be small, and we shall neglect the squares of the velocities due to f in comparison with their first powers. At the surface of the water let z be the depression at (x, y) below the mean level. Then
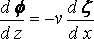 (1)
(1)
is the kinematic surface condition, and
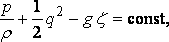
the equation of pressure, which, since
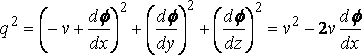 , .... (q.p.)
, .... (q.p.)
gives
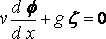
and, therefore, with (1)
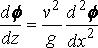 .... (2)
.... (2)
On account of the symmetry of the ship with respect to the median plane y = 0, we have d f/dy = 0 when y = 0, except over the ship, where, if h is the semi–breadth at (x, z),
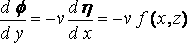 (say), ... (3)
(say), ... (3)
and this condition is taken to hold at the plane y=0, instead of at the surface of the .ship, the justification being the same as that for equation (I), Finally d f/dz = 0, at the bottom, z = h, of the water.
We now consider the solution for f, in the part of the water where y is positive, with the given boundary conditions at z=0, z=h, y=0.
The typical term in the solution is
a cos n ( z–h ) cos ( mx+ a ) cos ( py+ b ),
where m2+n2+p2=0. Here m must be taken real as the water extends from x = – ¥ to x = + ¥; n and p maybe either real or imaginary, but if p is imaginary [ =ip' ] the last factor must take the form e –p'y.
This term satisfies df/dz=0 at z=h, and it also satisfies equation (2), if
n tan nh = –v 2m 2/g ........ (4)
This equation has an infinite number of real roots and one pure imaginary root given by
n' tanh n'h = v 2m 2/g , [n = in'].
We shall see that the imaginary root is alone responsible for the wave–making resistance. As for p it is always imaginary for the real roots of n, and is so for the imaginary root if m > n'.
The condition (3) will now require the expansion of the given function f(x, z) in the form
åå amn cos n( z – h ) cos ( mx + a ),
where the summation with respect to m will take the form of an integral.
Suppose at first the function periodic in x so that
f ( x +l, z ) = f ( x – l, z ),
and put
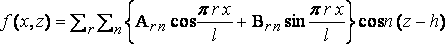 ,
,
where r is a positive integer.
By Fourier’s method
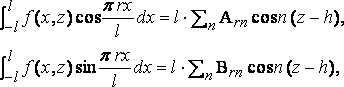
where A0n is to be halved as usual.
Since the functions cos n( z – h ) are all conjugate, as is easily proved, from these we get
and 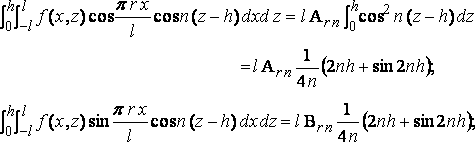
where A00 is to be halved; and the coefficients of the terms given by the imaginary roots, here, as always below, are got by pitting n=in'; so that

and so for Brn'.
Hence the theorem
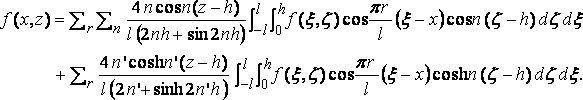
Now let l become infinite, and putting
p r/l=m
p/l=dm,
we get
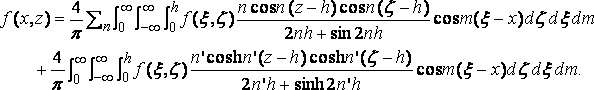
In particular, supposes the depth of water infinite, we have then
n h = r p + e ,
h dn = p ,
tan nh = tane,
cos n( z – h )= (–)rcos ( nz– e ),
2n + (sin 2n h ) / h = 2n,
n tan e = – km 2................... [k=v2/g],
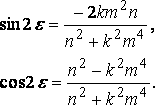
Also
tanh n'h = 1,
n = k m2,
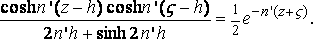
The result receives some confirmation from what has been observed with torpedo–boats at high speeds. It has been found that the total resistance varies as a power of the velocity which at first is nearly the second, but which, increasing to a maximum, ultimately Incomes less than the second [‡] . A very simple investigation, given below, shows that in shallow water, if we neglect all but the long waves, the wave–resistance varies ultimately as the first power of the velocity.
I may mention that somewhat similar work to that of the present paper gives a theory of the damping of the oscillations of ships due to wave–making. This I hope to give in a subsequent paper.
Substituting, we get
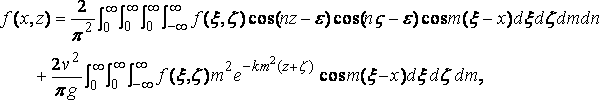
which is the theorem on which the rest of the present paper is build. It is curiously easy to give an á posteriory proof of the theorem. Using the value of e given above we find

Integrate the last two terms with respect to n, viz.
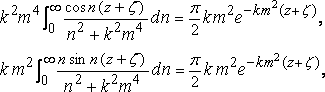
and the quadruple integral becomes
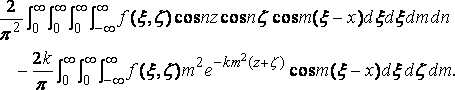
The former integral is f( x,z ), and the latter disappears with the triple integral in the given formula.
Considering now, for simplicity, the water infinitely deep, it appears at once that the required solution for f is
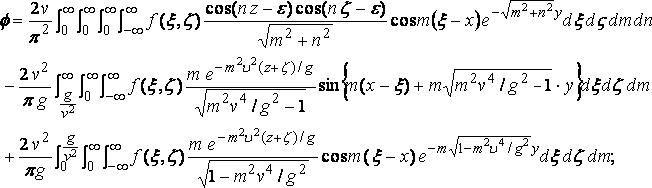 .... (5)
.... (5)
for this gives
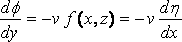 when y = 0.
when y = 0.
In this expression attention must be called to the factor
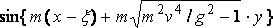
in the second integral. This form is not required to satisfy the boundary conditions formulated above; and it is evident the solution is to a certain extent indeterminate with those conditions, for we may superpose any system of free waves symmetrical with respect to y = 0 on a particular solution satisfying them. The form of the factor in question is chosen in order to make the elementary diverging waves trail aft; in other words, to satisfy the condition that the ship advances into still water.
Leaving the reduction of the integrals on one side, for the present, we proceed to calculate the wave–resistance ( R ).
Let dp be the increase of pressure duo to the wave–disturbance. Then
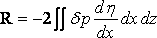 ,
,
the double integral extending over the median plane of the ship. Now measuring from the undisturbed surface
p = p + g r z – ½ r q 2 + ½ r v 2,
and therefore
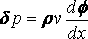 ... (q.p.)
... (q.p.)
so that
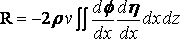 .
.
Substituting the value of d f/dx, we see that the first and third integrals in the expression for f add nothing to the resistance because
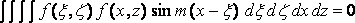 ,
,
on account of the odd factor sin m ( x – x ) , and hence
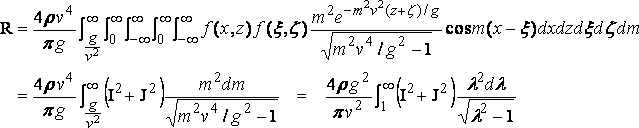 (6)
(6)
where l = mv2/g , and
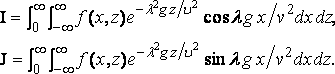
If the ship is similarly formed at bow and stern I = 0, the origin being at midship.
We can now prove that the resistance vanishes when the velocity is infinite.
Observe that
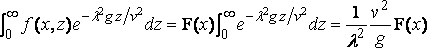 .... (7)
.... (7)
where F( x ) is less than the greatest value of f( x,z ) for a given value of x; and, therefore, if we substitute a large number t, instead ∞ as the upper limit of λ,, the part of R neglected is of order not greater than
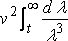 or v 2/t 2,
or v 2/t 2,
and this vanishes when v = ∞ if we take
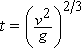 .
.
In the part of R retained l g/v 2 is small throughout, so that we may expand the circular functions and write
and 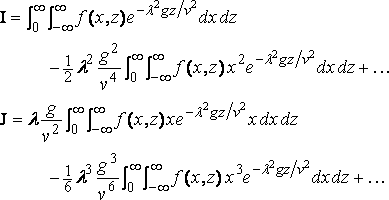
Now
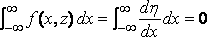 ,
,
the ship being of finite length and h = 0 at both ends. Hence, using the formula (7)
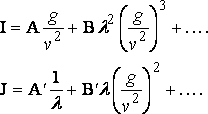
and 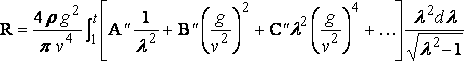
The successive terms are of orders
v–2 log v 2 , v –10/3 , …
and all vanish when v = ¥. The resistance therefore ultimately vanishes. Of course this result is only proved for a ship which is very short in comparison with [§] the depth of the water.
We now proceed to the reduction of the integral which gives the resistance duo to two elements of the surface.
Consider two elementary areas s, s' at ( x,z ), ( x',z' ) on the side of the ship, and lot θ, θ' be the inclinations of the horizontal lines in these areas to the axis of x. The resistance due to these two elements is
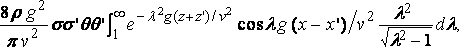
or, say, 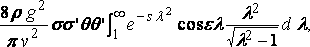
Now, writing for the moment z = x + i y, and taking the integral
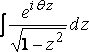
around the circuit enclosing the region x and y positive, we get
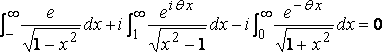 ,
,
and, therefore [§] , realizing,
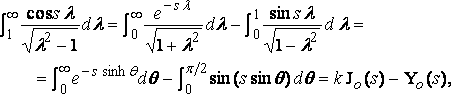 ..... .... (8)
..... .... (8)
where k = log 2 – g = .11593 … .
From which
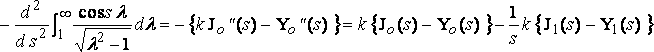 ,
,
since J0"(s) + J0'(s)/s + J0(s) = 0
J0'(s) = J1'(s)
[**] and so for Yo (s).
Now taking
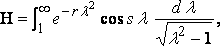
and putting
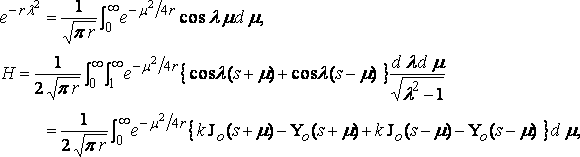 ... ... (9)
... ... (9)
from equation (8).
From which H can be readily calculated by mechanical quadrature in the case in which 4·r is not large, and. this is the case for ordinary ships. Elaborate tables of J0 and J1 are now available, and tables [**] of Y0 and Y1 have been calculated by Mr. B.A. Smith, who has kindly prepared tables of kJ0 – Y0 and kJ1 – Y1, appended to the present paper.
We now have
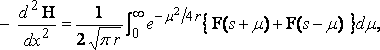
where 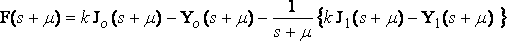 ,
,
and the expression for the mutual resistance is
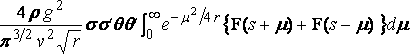 ,
,
where
r = g ( z + z' ) / v2,
s = g ( x – x' ) / v2.
For elements at opposite ends of the ship s will in general be large compared with unity and with
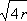 ; and in this case we can put
; and in this case we can put
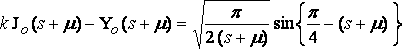 ... q.p.
... q.p.
and so for ( s – m ) and then approximately
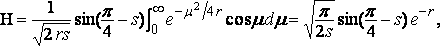
and the resistance is
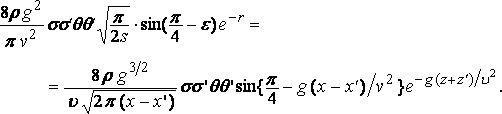
Now if l is the length of the free wave which travels with the velocity of the ship
v2 = g l / 2 p ,
and the formula can be written
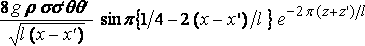 .
.
This gives a maximum resistance, approximately, when
x – x' = ( n+7/8 )·l .......... [n an integer]
and a maximum assistance when
x – x' = ( n+3/8 )·l.
These formula correspond to the interference of the bow and stern waves, which has been so skillfully discussed by Mr. R.E. Froude. When the two elements are on the same vertical cross–section of the ship, another form of reduction may be given. Putting x – x' = 0, the integral to be considered is
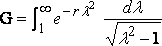 .
.
Put
l2 = ½ ( 1+ m),
so that 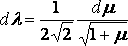 ,
,
and l2 = ½ (m
– 1 );
whence 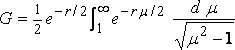
or, if m = cosh f ,
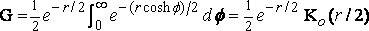 ,
,
where K0 is the Bessel function, so indicated by Gray and Mathews (pp. 67, 90).
Hence
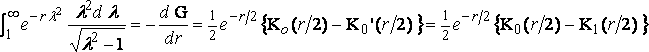 ,
,
since K0' = K'1 , and the corresponding term in the resistance is
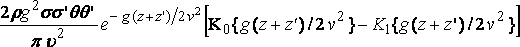
The functions K do not appear to have been calculated, but their general course is known. It will be sufficient at present to refer to Gray and Mathews, chap. vii.
As an illustration of the process of calculating the resistance of a given ship at any speed, we may consider one of simple analytical form which is fairly ship–shape and easily realisable. Experimental confirmation of the result was not practicable, and the matter must be left in the hands of those who have the necessary apparatus at command.
Let the surface of the ship be
y = ±c ( 1 + cos ax )( 1 + cos bz ),
between
x=± p /a,
z = 0 and p /b;
Fig. 2.

so that, for y positive,
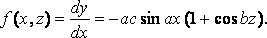
Here I = 0, and
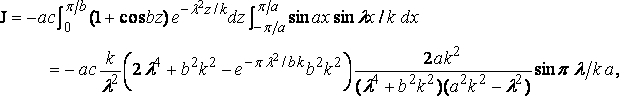
where k = v2/g; and therefore
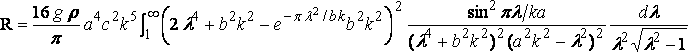
which is best calculated by mechanical quadrature.
Suppose, for example, in foot–second units
v = 20 (velocity of ship),
2 p /a = 200 (length of ship),
p /b = 20 (depth below water–line),
8c = 32 (greatest breadth),
then the integral is found to be 620, and the resistance is R=940 lbs. wt. about.
This seems to be about what one would expect from the experimental results available; but I know of no formula with which to compare it, and experiment alone can decide whether the theory has numerical value. Of course the method of successive approximations can be applied if necessary.
To examine the case of the ship in shallow water in which all but the long waves are neglected, we may proceed as follows: – We make the motion steady as before and use the same set of axes. The pressure–equation gives at the surface
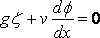 , as before ;
, as before ;
while the equation of continuity for long waves gives
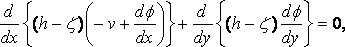
where h is the depth of the water, and this is
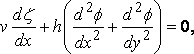 ... (q.p.)
... (q.p.)
Differentiating with respect to x and substituting for f from the pressure–equation, we obtain
or 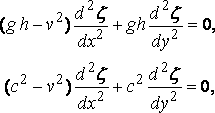
where c is the velocity of free long waves.
The ship being wall–sided, and extending to the bottom of the water, the kinematic equation over the ship is
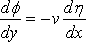 ,
,
which on differentiation with respect to x and use of the pressure–equation gives
and, of course, 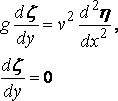
over the rest of the plane y = 0.
Now if v > c, i.e. if the velocity of the ship is greater than that of the free wave, the equation
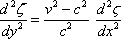
is solved in the form 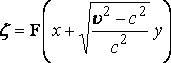 .... (10)
.... (10)
where the boundary condition gives
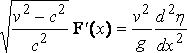 ,
,
or 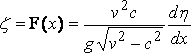 ... .... (11)
... .... (11)
The form of solution (10) is employed in order to make the diverging waves trail aft.
The disturbance therefore consists of two bands at an angle 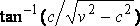 with the line of
the ship’s motion, the front of each band being a hump above the mean level and its back part a hollow, which is similar
to the hump if the ship is similarly shaped fore and aft.
with the line of
the ship’s motion, the front of each band being a hump above the mean level and its back part a hollow, which is similar
to the hump if the ship is similarly shaped fore and aft.
The resistance (R) is given by
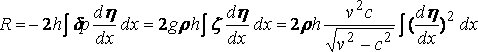 ,
,
so that it is infinite when the velocity of the ship is equal to that of the free wave, and ultimately varies as the velocity.
If v < c , the differential equation for z takes the potential form
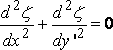 ,
,
putting 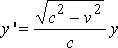 .
.
The solution is now
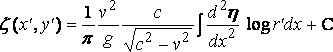 ,
,
where r' 2 = ( x' – x )2 + y' 2, and there is no wave–resistance.
If we add the solutions for an equally–spaced infinite number of ships moving abreast, we get the case of a ship in the centre of a canal.
In the Table appended there may be an error of 1 in the last place or possibly of 2 in the values for x > 3 or 4.
Melbourne University, August 9, 1897.
Tables of k Jo – Y o and k J1 – Y1. By Mr. B. A. Smith, M.C.E.
| x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) | x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) |
| .00 | ∞ | ∞ | .41 | .9243 | 2.7384 |
| .01 | 4.7200 | 100.0261 | .42 | .8972 | 2.6822 |
| .02 | 4.0274 | 50.0453 | .43 | .8706 | 2.6286 |
| .03 | 3.6215 | 33.3951 | .44 | .8446 | 2.5773 |
| .04 | 3.3331 | 25.0767 | .45 | .8190 | 2.5282 |
| .05 | 3.1091 | 20.0903 | .46 | .7940 | 2.4813 |
| .06 | 2.9258 | 16.7695 | .47 | .7694 | 2.4362 |
| .07 | 2.7705 | 14.4002 | .48 | .7453 | 2.3929 |
| .08 | 2.6359 | 12 6255 | .49 | .7216 | 2.3514 |
| .09 | 2.5168 | 11.2470 | .50 | .6983 | 2.3111 |
| .10 | 2.4099 | 10.1457 | .51 | .6753 | 2 2729 |
| .11 | 2.3133 | 9.2459 | .52 | .6528 | 2.2357 |
| .12 | 2.2245 | 8.4971 | .53 | .6306 | 2.1999 |
| .13 | 2.1428 | 7.8645 | .54 | .6088 | 2.1653 |
| .14 | 2.0670 | 7.3230 | .55 | .5873 | 2.1319 |
| .15 | 1.9961 | 6.8545 | .56 | .5661 | 2.0995 |
| .16 | 1.9297 | 6.4450 | .57 | .5453 | 2 0681 |
| .17 | 1.8671 | 6.0843 | .58 | .5248 | 2.0377 |
| .18 | 1.8079 | 5.7642 | .59 | .5046 | 2 0083 |
| .19 | 1.7517 | 5.4780 | .60 | .4816 | 1.9798 |
| .20 | 1.6982 | 5.2209 | .61 | .4650 | 1.9521 |
| .21 | 1.6472 | 4 9888 | .62 | .4456 | 1.9251 |
| .22 | 1.5983 | 4.7779 | .63 | .4264 | 1.8988 |
| .23 | 1.5515 | 4.5855 | .04 | .4076 | 1.8732 |
| .24 | 1.5066 | 4.4091 | .65 | .3890 | 1.8483 |
| .25 | 1 .4633 | 4.2476 | .66 | .3707 | 1.8241 |
| .26 | 1.4216 | 4 0983 | .67 | .3525 | 1.8005 |
| .27 | 1.3813 | 3.9603 | .68 | .3346 | 1.7775 |
| .28 | 1.3424 | 3.8323 | .69 | .3169 | 1.7550 |
| .29 | 1.3046 | 3.7131 | .70 | .2995 | 1.7329 |
| .30 | 1.2680 | 3.6020 | .71 | .2823 | 1.7114 |
| .31 | 1.2326 | 3.4982 | .72 | .2653 | 1.6904 |
| .32 | 1.1981 | 3.4007 | .73 | .2485 | 1.6699 |
| .33 | 1.1645 | 3.3091 | .74 | .2319 | 1.6496 |
| .34 | 1.1319 | 3.2233 | .75 | .2155 | 1.6299 |
| .35 | 1.1000 | 3.1423 | .76 | .1993 | 1.6105 |
| .36 | 1.0690 | 3.0656 | .77 | .1833 | 1.5914 |
| .37 | 1.0387 | 2.9932 | .78 | .1675 | 1.5728 |
| .38 | 1.0092 | 2.9245 | .79 | .1518 | 1.5544 |
| .39 | .9803 | 2.8593 | .80 | .1363 | 1.5365 |
| .40 | .9519 | 2.7973 | .81 | .1211 | 1.5188 |
Table (continued).
| x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) | x. | k Jo(x)–Yo(x) | k J1(x)–Y1(x) |
| .82 | .1060 | 1.5015 | 4.8 | .4277 | –.3354 |
| .83 | .0910 | 1.4913 | 4.9 | .4588 | –.2817 |
| .84 | .0763 | 1.4674 | 5.0 | .4846 | –.2323 |
| .85 | .0617 | 1.4509 | 5.1 | .5052 | –.1786 |
| .86 | .0473 | 1.4346 | 5.2 | .5203 | –.1214 |
| .87 | .0330 | 1.4185 | 5.3 | .5300 | –.0690 |
| .88 | .0189 | 1.4026 | 5.4 | .5343. | –.0159 |
| .89 | .0050 | 1.3870 | 5.5 | .5332 | +.0373 |
| .90 | –.0088 | 1.3715 | 5,6 | .5269 | .0892 |
| .91 | –.0224 | 1.3563 | 5.7 | .5155 | .1393 |
| .92 | –.0359 | 1.3113 | 5.8 | .4991 | .1873 |
| .93 | –0493 | 1.3261 | 5.9 | .4782 | .2326 |
| .94 | –.0625 | 1.3117 | 6.0 | .4527 | .2749 |
| .95 | –.0756 | 1.2972 | 6.1 | .4232 | .3139 |
| .96 | –.0885 | 1.2829 | 6.2 | .3900 | .3492 |
| .97 | –.1012 | 1.2688 | 6.3 | .3535 | .3805 |
| .98 | –.1138 | 1.2548 | 6.4 | .3140 | .4077 |
| .99 | –.1263 | 1.2108 | 6.5 | .2721 | .4306 |
| 1.0 | –.1386 | 1.2271 | 6.6 | .2281 | .4488 |
| 1.1 | –.2548 | 1.0966 | 6.7 | .1826 | .4625 |
| 1.2 | –.3583 | .9757 | 6.8 | .1358 | .4715 |
| 1.3 | –.4501 | .8616 | 6.9 | .0881 | .4758 |
| 1.4 | –.5304 | .7526 | 7.0 | ..0408 | .4755 |
| 1.5 | –.6008. | .6177 | 7.1 | –.0065 | .4704 |
| 1.6 | –.6604 | .5160 | 7.2 | –.0531 | .4609 |
| 1.7 | –.7101 | .4173 | 7.3 | –.0986 | .4471 |
| 1.8 | –.7500 | .3513 | 7.4 | –.1424 | ..4290 |
| 1.9 | –.7805 | .2583 | 7.5 | –.1842 | .4071 |
| 2.0 | –.8017 | .1682 | 7.6 | –.2237 | .3814 |
| 2.1 | –.8142 | .0812 | 7.7 | –.2604 | .3524 |
| 2.2 | –.8180 | –.0023 | 7.8 | –.2910 | .3203 |
| 2.3 | –.8138 | –.0821 | 7.9 | –.3243 | .2854 |
| 2.4 | –.8017 | –.1580 | 8.0 | –.3510 | .2484 |
| 2.5 | –.7824 | –.2293 | 8.1 | –.3739 | .2093 |
| 2.6 | –.7560 | –.2959 | 8.2 | –.3928 | .1684 |
| 2.7 | –.7234 | –.3576 | 8.3 | –.4076 | .1206 |
| 2.8 | –.6848 | –.4139 | 8.4 | –.4182 | .0840 |
| 2.9 | –.6407 | –.4619 | 8.5 | –.4214 | .0408 |
| 3.0 | –.5920 | –.5100 | 8.6 | –.4264 | –.0020 |
| 3.1 | –.5390 | –.5492 | 8.7 | –.4242 | –.0438 |
| 3.2 | –.4823 | –.5823 | 8.8 | –.4177 | –.0851 |
| 3.3 | –.4227 | –.6092 | 8.9 | –.4071 | –.1251 |
| 3.4 | –.3606 | –.6299 | 9.0 | –.3926 | –.1637 |
| 3.5 | –.2970 | –.6444 | 9.1 | –.3744 | –.2001 |
| 3.6 | –.2320 | –.6525 | 9.2 | –.3527 | –.2343 |
| 3.7 | –.1666 | –.6546 | 9.3 | –.3277 | –.2657 |
| 3.8 | –.1014 | –.6505 | 9.4 | –.2996 | –.2940 |
| 3.9 | –.0368 | –.6406 | 9.5 | –.2688 | –.3194 |
| 4.0 | +.0266 | –.6251 | 9.6 | –.2359 | –.3412 |
| 4.1 | +.0881 | –.6042 | 9.7 | –.2012 | –.3594 |
| 4.2 | .1472 | –.5781 | 9.8 | –.1642 | –.3738 |
| 4.3 | .2035 | –.5472 | 9.9 | –.1261 | –.3845 |
| 4.4 | .2566 | –.5120 | 10.0 | –.0874 | –.3912 |
| 4.5 | .3058 | –.4728 | 10.1 | –.0181 | –.3911 |
| 4.6 | 3510 | –.4300 | 10.2 | –.0087 | –.3923 |
| 4.7 | .3917 | –.3812 | 10.3 | +.0302 |
[*] Communicated by the Author.
[†] 'On the Leading Phenomena of the Wave–Making Resistance of Ships'.
Trans.Inst.Naval Architects, 1881
[‡] White, p. 470
[§] See Gray and Mathews, 'Bessel Functions' p.65, and Ex.18, p.230. The
formula (8) was given by Weber.
[**] ‘Messenger of Mathematics,’ 1896.
Philosophical Magazine, 1898, vol. 45, Sec. 5, pp. 106–123.
Phil. Mag, S, .5. Vol . 45 No. 272. Jan. 1898. K