Трехмерная тензорная математика вычислительных экспериментов в гидромеханике
2. Логика создания вычислительных моделей и компьютерных алгоритмов
Построение программной среды для проведения вычислительного эксперимента
Определение цели, содержания и методологии проектирования вычислительного эксперимента
Проектные решения для новых алгоритмов вычислительной гидромеханики
Особенности языковой среды программирования
О логическом проектировании программных комплексов
Особенности использования логической матрицы проекта
Среда программирования на основе языка С++
Вычислительные операции с элементарными жидкими частицами, их физическая интерпретация
Построение числовых массивов для моделирования пространственных гидродинамических полей
«Так как древние, по словам Паппуса[1], придавали большое значение механике
при изучении природы, то новейшие авторы, отбросив субстанции и скрытые
свойства, стараются подчинить явления природы законам математики.
В этом сочинении имеется в виду тщательное развитие приложений
математики к физике. Древние рассматривали механику двояко:
как рациональную (умозрительную), развиваемую точными
доказательствами, и как практическую. К практической механике
относятся все ремесла и производства, именуемые механическими,
от которых и получила свое название и сама механика.
… и если кто-нибудь смог исполнить свое изделие с совершеннейшей
точностью, то был бы наилучшим из всех механиков».
Исаак Ньютон[2]
Следуя обязательному правилу о сквозной механико-геометрической интерпретации всех числовых объектов и операций, выполняемых на ЭВМ при проведении вычислительного эксперимента, можно сформулировать основные требования, которые должны соблюдаться на этапе проектирования новых алгоритмов и программных комплексов для проведения прямого моделирования прикладных задач механики сплошных сред:
1) Элементарные объекты гидромеханики должны определяться только в размерной форме;
2) Вычислительные операции должны быть определены в строгой взаимосвязи физических свойств жидкости и законов механики, которые могут применяться в условиях автоматического пересчета физических размерностей и преобразования координатных величин;
3) Свойства вычислительных операций и элементарных числовых объектов определяются как в единой – абсолютной системе координат, так и в локальных - дуальных базисах, связанных с конкретными частицами жидкости.
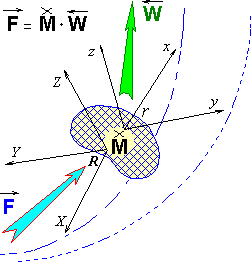 Формально, на разделенных во времени этапах вычислительного эксперимента в механике сплошных сред, может быть введен своеобразный векторный аналог Закона Ньютона, определенного с помощью тензорной операции умножения, где внешняя сила F задается в абсолютной системе координат, а реакция W – уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы M будет не только аккумулировать энергию поступательного движения, но также определит инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
Формально, на разделенных во времени этапах вычислительного эксперимента в механике сплошных сред, может быть введен своеобразный векторный аналог Закона Ньютона, определенного с помощью тензорной операции умножения, где внешняя сила F задается в абсолютной системе координат, а реакция W – уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы M будет не только аккумулировать энергию поступательного движения, но также определит инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
С позиций классической механики такая формализация означает лишь тот факт, что на разных этапах вычислений используются не суммарные внешние воздействия на малые подвижные и деформируемые частицы жидкости, а лишь те, которые доступны в численных схемах разделения движения по физическим процессам, определяемым при постановке вычислительной задачи в рамках строго линейных аппроксимационных законов. В данном случае подразумевается, что на первом этапе дифференцирование первого порядка для векторов смещений жидких частиц переопределяет их собственную кинематику, тогда аналогичное дифференцирование скоростей их перемещения позволит учесть инерционные (силовые) свойства взаимодействия между исходными частицами жидкости. Если в таком двойном дифференцировании поле скорости вычисляется по фиксированным узлам эйлеровой координатной сетки и соотносится к центрам масс крупных частиц жидкости, то инерционные характеристики движения этих частиц будут снова сведены к тем же узлам, но сильно сместившимся за расчетный интервал времени.
Вычислительные модели гидромеханики в каноническом представлении удобно формализовать с помощью линейных аппроксимирующих функций, точные физические величины которых определяются на разреженных узлах конечно-разностной сетки, охватывающей ограниченную область течения жидкости. Аналитические методы времен Исаака Ньютона позволяли в разностной форме выполнить постановку и прямое численное решение многих интерполяционно-динамических задач. Однако, несмотря на эффективность и универсальность ньютоновских численных решений, это направление математических исследований сдерживалось необходимостью применения сложных численно-логических схем (алгоритмов) и трудоемкостью прикладных вычислительных задач.
Современная компьютерная логика позволяет обобщить разностные методы решения задач гидромеханики с помощью методов функционального программирования, традиционно используемого в системах искусственного интеллекта.
Для явного контроля физических процессов законы движения жидкости будут изначально представляться в жестких логических операциях трехмерной тензорной арифметики, оперирующих конкретными параметрами течения в размерном виде. Трехмерный тензорный вычислительный аппарат формализует описание явлений гидромеханики именно для того случая, когда непрерывные функции определяются с помощью ограниченного количества не очень близко расположенных аппроксимирующих пространственно-временных точек.
Важным преимуществом такой постановки вычислительного эксперимента в гидромеханике явилась возможность более глубокого понимания многих законов и явлений, сопровождающих течение реальных жидкостей. Разработка же формализованных правил для компьютерной реализации вычислительных экспериментов в тензорной постановке сама по себе составила интереснейшую задачу, которая позволила вновь коснуться как математических основ гидромеханики, так и фундаментальных понятий физики в целом. Оказалось, что тензорная арифметика и логика вычислительных операций позволяют проследить физические аналогии всех вычислительных операций и построить комплекс алгоритмических объектов наиболее полно определяющих суть и форму вычислительных процессов при моделировании физических явлений и механики жидкости.
При построении новых математических операций и вычислительных объектов не будет использовано никаких новых гипотез об относительности систем отсчета и неопределенности внутренних свойств жидкости. Главная или общая система координат является всегда ортогональной и ортонормированной. Отсчеты времени всегда задаются скалярными величинами и используются только для фиксации во времени всего вычислительного процесса, и лишь при особых оговорках, уточненного состояния его отдельных подобластей или жидких частиц.
Исходное пространство и время всегда наделяются свойствами идеальности, то есть, эти системы отсчета всегда глобальны и абсолютны по проявлениям, непрерывны, линейны и недеформируемы по своим внутренним свойствам. Пространство не терпит пустоты и при необходимости заполняется условным эфиром, в качестве носителя законов математической теории поля, со свойствами вязкой, упругой и сжимаемой жидкости.
Физические размерности для полей и частиц гидромеханики являются естественным и наилучшим предикатом в формализациях элементарных вычислительных объектов. Такие же определители ‑ предикаты необходимы для фиксации типа и связности координатных базисов, для автоматизированного определения текущей системы координат и пространственной привязки к конкретной крупной частице жидкости.
В комплексе вся система признаков-предикатов необходима для автоматизированного распознавания и применения базовых функций для трансформации элементарных числовых объектов к требуемому или условно каноническому виду. В последующем, формализованные числовые объекты смогут быть задействованы в реализации или согласовании законов гидромеханики, или подвергнуты простому преобразованию к заданной системе отсчета и физической размерности.
С каждой частицей жидкости связывается собственная локальная система координат с теми же внутренними свойствами, что и единая абсолютная система отсчета. Локальная и абсолютная системы координат строго связаны между собой едиными динамическими свойствами и физическими размерностями наполняющих их жидкостей, а также с помощью строгих правил выполнения тензорных математических операций и преобразований.
Традиционная физическая интерпретация, так же как и численное решение задач гидромеханики, опирается на два взаимосвязанных и существенно отличающихся по форме геометрических представления о течении жидкости, - это известные дифференциальные формализации течений по Эйлеру – на фиксированной сетке и изменяющихся значениях гидродинамических полей, и по Лагранжу – с фиксацией законов сохранения внутри каждой из движущихся частиц жидкости.
Опыт реализации вычислительных экспериментов показывает, что для сложных расчетных областей невозможно применение дифференцирующих разностей более чем первого порядка. Задачи же механики опираются на уравнения движения второго порядка, которые в случае задач аэрогидромеханики довольно уверенно моделируются с использованием разделения решения на подэтапы, где последовательное использование интерполирующих функций первого порядка сначала опирается на неподвижные узлы сетки, затем ведется расчет в локальных координатах подвижных частиц жидкости. Такой подход к решению соответствует классическому разложению дифференциальных уравнений гидромеханики по физическим параметрам, который выполняется в лагранже-эйлеровых схемах, в методе «Крупных частиц» или «Конечного объема». Суть разложения по физическим параметрам, при таком подходе, выражается в двойном последовательном интегрировании уравнений движения первого порядка, что, в свою очередь, разделяет каждый временной цикл вычислительного эксперимента на три этапа:
1 этап – вычисляются кинематические параметры для динамических центров крупных частиц жидкости, для чего используются текущие исходные данные в неподвижных узлах конечноразностной расчетной сетки, которая обычно обладает свойствами неподвижных эйлеровых координат;
2 этап – лагранжевы или крупные деформируемые частицы жидкости участвуют в свободном движении, перераспределяя внутренние свойства исходных эйлеровых ячеек по смежному с ними пространству;
3 этап – согласуются законы сохранения массы и энергии, что достигается поляризацией или деформацией сдвинутых частиц жидкости, с последующей переинтерполяцией характеристик течения в исходные узлы неподвижной эйлеровой расчетной сетки.
Для построения вычислительного эксперимента по указанной схеме каждая из частиц жидкости должна вести себя как своеобразный энергоемкий объект, подчиняющийся законам сохранения энергии в пределах геометрического объема этой частицы, часть которой тратится на простую передачу движения смежным частицам, а часть на консервацию энергии движения внутри самой элементарной частицы жидкости. Последнее может проявляться как безвозвратная потеря энергии движения на трение при деформации жидкой частицы, а также как аккумулируемая энергия, в том числе обусловленная изменением интенсивности замкнутых течений внутри такой элементарной частицы жидкости (образование/затухание внутренних диполей).
Элементарные объекты гидромеханики и связанные с ними вычислительные операции определяются в одной из трех числовых форм:
1) Скаляр – числовая величина, не зависящая от системы отсчета, являющаяся либо инвариантом пространственно-временных преобразований, либо эмпирической величиной, формализующей реологические свойства жидкости (в обобщенном случае это одно и то же). Может использоваться только в операциях произведения, с любыми объектами;
2) Вектор – числовой объект, задает пространственно ориентированное внешнее воздействие или реакцию на него со стороны элементарной жидкой частицы. Векторные величины всегда связаны с конкретным пространственным базисом. Допускаются операции сложения для величин, измеренных в одной и той же системе отсчета и с одинаковыми физическими размерностями, а также операции умножения векторов на тензоры, в результате которых происходит замена или уточнение опорного базиса;
3) Тензор II ранга – является сложной производной величиной, характеризующей локальные свойства геометрических преобразований, или фиксирующей динамическое состояние элементарной жидкой частицы. Тензорные объекты можно интерпретировать в качестве пространственных базисов, которые хранят геометрию деформирующейся жидкой частицы, и задают их локальную (внутреннюю) кинематику и конвективные свойства течений жидкости в целом.
Тензоры всегда участвуют в анализе динамических свойств и режимов течения реальной жидкости. Любые преобразования тензорных величин выполняются только в соответствии с логикой представления физических процессов и законов гидромеханики. Тензорные операции могут определяться чисто лингвистическими правилами языков программирования (их внутренней семантикой), что позволяет в процессе вычислительных экспериментов задействовать гибридные математические модели или параллельно использовать существенно различающиеся гидродинамические модели течения.
Главным объектом исследования является конечный объем подвижной и деформируемой сплошной среды (крупная частица или конечный объем жидкости), заключенной в геометрическое пространство, ограниченное симплексом из смежных узловых точек (рис. 2.1).
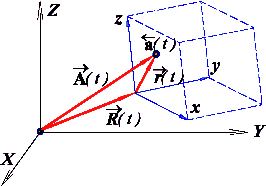
Рис. 2.1. Геометрическое положение в пространстве элементарного вычислительного объекта (малого континуума), образованного триадой координатных векторов локального базисного тензора.
Такие частицы жидкости образуют элементарные или базисные объекты вычислительной гидромеханики, с которыми связываются реологические, инерционные и энергетические свойства локальных течений. Внутри элементарной частицы, в строгой форме определяются законы независимого существования и взаимодействия между смежными объектами сплошной среды.
Симплекс из трех ортогонально ориентированных пространственных разностей математически определяется в форме тензора II ранга, который задает локальный базис для фиксации внутренних свойств жидкой частицы. Физические свойства жидкости внутри элементарной расчетной частицы с помощью тензорных произведений могут однозначно переопределяться в единую для всех других частиц глобальную систему отсчета.
Для поиска механизмов взаимодействия смежных и дальних частиц жидкости или твердых тел, уже необходимы точные правила перестроения систем отсчета с помощью линейных и обратных математических операций, что возможно только с привлечением логически сложных функциональных зависимостей (тензоров), задающих условия взаимодействия частиц, участвующих в неразрывном течении жидкости.
Геометрически частица жидкости {  -1} может быть представлена в виде условного параллелепипеда (в обратной задаче - эллипсоида), внутреннее состояние которого формализуется линейными или обратными
распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных локальных базисов в форме трехмерных тензоров II ранга, задающих линейное (или обратное) распределение внутренних свойств течения между жидкими частицами, однозначно определяемых интерполяционными (без экстраполяции) зависимостями между исходными узлами расчетной области.
-1} может быть представлена в виде условного параллелепипеда (в обратной задаче - эллипсоида), внутреннее состояние которого формализуется линейными или обратными
распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных локальных базисов в форме трехмерных тензоров II ранга, задающих линейное (или обратное) распределение внутренних свойств течения между жидкими частицами, однозначно определяемых интерполяционными (без экстраполяции) зависимостями между исходными узлами расчетной области.
Воспользуемся обобщенным базисом троичной логики для формального представления объекта исследований, целью которого является изучение возможности комплексного решения задачи о проведении вычислительного эксперимента в гидромеханике, где математический аппарат должен быть строго согласован с алгоритмическим описанием физических процессов, и обеспечивать эффективное (или автоматизированное) проектирование численных схем и алгоритмов для решения как прямых, так и обратных задач гидромеханики.
Сложные вычислительные эксперименты в гидромеханике не могут быть реализованы с помощью простых линейных повторений математических формул. Без следования теоретическим правилам при построении алгоритмов взаимодействия функций и процедур компьютерной программы, без строгого согласования форматов данных, определяющих элементарные вычислительные объекты, разработка сложного комплекса компьютерных программ может остановиться на невыносимо трудной отладке или неустранимых несоответствиях между вычислительными объектами и операциями. В отличие от изложения методов решения задач с использованием естественных языков, при разработке сложных систем в языках программирования недопустимо даже малейшего отклонения от логических законов или упущений при формализации моделируемых физических процессов.
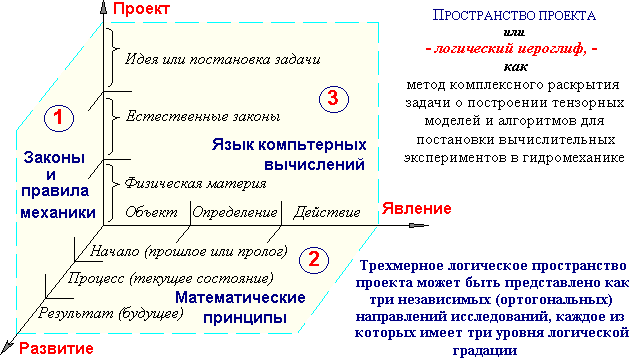
Рис. 2.2. Логическое пространство проектной задачи
о построении вычислительного эксперимента в гидромеханике.
На рисунке 2.2 представлено трехмерное логическое пространство, базисные плоскости которого образуют главные направления проектных исследований, которые должны быть в полной мере определены и представлены в виде единого комплекса логических связей, объектов и алгоритмов. Секторы, образованные градациями по направлениям, определяют внутреннее строение и условные названия конкретных этапов разработки, служебных программ, процедур и функций, определяемых на конкретных языках программирования.
Такой троичный базис позволяет согласовать противоречия при использовании встречных подходов к проектированию сложных логических систем. С этой целью противоречивые требования соотносятся между собой с позиций третьего - ортогонального и независимого от двух первых методологических подходов. С позиций такого третьего направления, названного к примеру: «Проект», могут быть согласованы (ортогонализованы) противоречия при представлении законов механики с использованием конкретных языков программирования. На самых верхних (дальних) уровнях в направлении «Проекта» должны решаться вопросы принципиальной возможности точного определения законов механики с использованием языков программирования, чем должно обеспечиваться не только их взаимное согласование, но также и должное развитие, устраняющее исходные противоречия. В этом случае, на среднем уровне будут согласованы противоречия в плоскости «Естественные законы», что обеспечит постановку прикладной физической задачи в терминах формализованной «Физической материи».
В результате полной проработки решаемой прикладной задачи, различные логические подходы должны привести к оптимальному проектированию программно-технического комплекса в целом, в котором исходные физические парадоксы и формальные противоречия должны образовать всесторонне согласованную среду для проведения прямых вычислительных экспериментов.
Пусть, к примеру, одним из ключевых понятий решаемой задачи будет выступать описание гидродинамических процессов вдоль оси «Явление», используемого по правилам «существительного» в предложении естественного языка, и ось-определение «Развитие», соотносимое с понятием «процесса» или «действия», – подобно глаголу. Тогда плоскость оси «Проект» будет выступать в роли логического поля для согласования свойств вычислительных объектов и алгоритмических операций в целом, определяя общую основу обоих подходов к численному решению конкретной прикладной задачи гидромеханики.
К логическому базису можно применять метафизические преобразования, аналогичные стандартным операциям тензорного анализа с учетом физических размерностей и соглашений об абсолютной и локальной системе отсчета. Полученные таким образом метафизические правила преобразования логических тензоров (матриц) могут быть использованы для разделения алгоритмов компьютерных вычислений на функциональные и декларативные методы программирования, в соответствии с требованиями по интерпретации исходных данных (существительных) и математических операций (глаголов).
По условиям проектирования «снизу-вверх» - направление от плоскости «Проект-Развитие», может быть изучена систематизация законов гидромеханики и тензорного анализа с позиций логики вычислительных операций. Это необходимо для формального определения гидродинамических величин и объектов, базисов и пространства их существования и областей для определения числовых величин, которые должны быть связаны жесткими правилами тензорных арифметических операций и вычислительных алгоритмов для автоматических преобразований при изменении систем отсчета или физических размерностей. Реальные вычислительные модели и их свойства могут быть рассмотрены в соответствии с другим ортогональным (независимым) направлением вдоль оси к плоскости «Развитие-Явление», и на котором строится обоснование достаточности аргументов (исходных условий) при теоретическом обосновании нового математического аппарата вычислительной гидромеханики. Ось «Явление-Проект» может быть ассоциирована с изучением специализированного языка программирования для решения задач вычислительной гидромеханики, который должен быть спроектирован и реализован для наиболее эффективного использования законов и математических принципов формализованных в двух других ортогональных плоскостях (независимых направлениях исследований), в рамках единого троичного логического базиса (настоящего исследования).
Плоскость «Язык компьютерных вычислений» находится в стадии перспективного проектирования, являясь источником и целью излагаемой здесь «Трехмерной тензорной математики вычислительных экспериментов», поэтому данный вопрос должен включать три подраздела, образующих диагональную или каноническую матрицу исходного проекта. Каноническая ‑ в данном случае означает, что логическая матрица построена в идеализированном или собственном базисе для исследования проекта тензорного языка программирования. На практике поиск таких упрощенных условий может быть начат с эвристических начальных предположений для реализации процедур «прямого хода» проекта, который должен методично корректироваться за счет «обратного решения», означающего дальнейшую детализацию и формализацию условий, необходимых для построения новых методов практической реализации вычислительных экспериментов в гидромеханике.
В плоскости «Проект - Развитие» à «Законы и правила механики» выполняется определение вычислительного эксперимента как полноценной модели физического «Явления», моделируемого с помощью логических объектов и операций цифровой дискретной ЭВМ.
Формально, методология построения «тензорной математики» представляется по правилу проектирования «сверху-вниз», которое возможно при условии, что основные математические инструменты и вычислительные алгоритмы уже известны и опробованы на практике. Соответственно при проектировании «снизу-вверх», недостающие инструментальные средства могут быть должным образом доработаны, что не снимет ограниченности результата, обусловленного недостатком исходных знаний.
Учитывая, что в этом случае каждый элемент троичной матрицы становится элементом самостоятельного исследования и законченного повествования, изложение материала может быть максимально кратким для верхних строк матрицы, и расширяться по мере приближения к практическим вопросам, разрешаемым в нижних строках троичной матрицы.
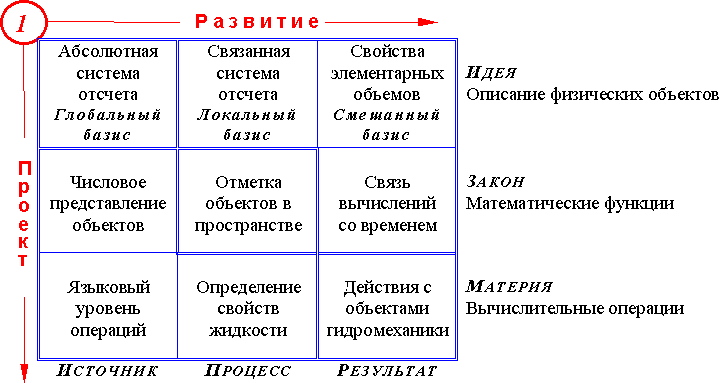
Рис. 2.3. Структура троичной матрицы, определяющей взаимосвязь проектных элементов для построения сложных программ вычислительной гидромеханики, с указанием условно применяемых к ним математических операций и логики пространственно-временных преобразований.
Приведенная на рисунке 2.3 схема построения вычислительного эксперимента может быть представлена в виде трех уровней аппаратной и языковой поддержки различных методов программирования, создаваемых по принципу от «множества расчетных алгоритмов» к «унифицированной функциональной среде», ориентированной на внутренний контроль и согласование реологических свойств жидкости, и автоматизированную численную реализацию законов механики сплошной среды.
Для определения языковой среды программирования можно воспользоваться обобщенными смысловыми понятиями [Уинстон, 1980], что позволит проводить аналогии с естественным мышлением при анализе новых проектных решений. Формально и упрощенно разделим программные процедуры на «алгоритмические» ‑ имеющие неизменный программный код, бесконтрольно применяемый к любым числовым данным, и на «функциональные» ‑ в которых исполняемый код автоматически адаптируется и перенастраивается под особенности текущего состояния элементарных числовых объектов механики сплошной среды.
Алгоритмический язык. Может быть представлен как запись командных или определяющих предложений, которые имеют однозначный смысл, существенный порядок слов и неизменную форму в процессе выполнения компьютерной программы. К алгоритмическим языкам относятся все общедоступные языки программирования, такие как Fortran, Pascal, C и С++. Базовыми операциями этих языков являются определения и преобразования числовых данных, управляемые линейными алгоритмами. Если фрагмент текста программы оформляется в виде отдельной процедуры, то внутренние числовые данные временно располагаются в стековой памяти или образуют статические поля собственных переменных, прямо влияющих на ход вычислений. Таким образом, несмотря на жесткое сохранение формы языковых конструкций, в процессе выполнения программы присутствует сильнейшая контекстная зависимость для всех слов языка программирования, а нередко и для всех процедур и функций внутри конкретного программного комплекса.
Если при построении программы на алгоритмических языках используется аппарат глобальных ссылок и обращение к общедоступной памяти типа «куча», то обобщенный анализ вычислительных алгоритмов затрудняется их чрезмерной взаимозависимостью. Современные объектно-ориентированные методы программирования, вместо логической оптимизации и обеспечения функциональной независимости отдельных процедур, используют метод автоматизированного загромождения тела программы многократным повторением формально одинаковых фрагментов машинного кода. Такой подход неприемлем для построения прямых вычислительных экспериментов в гидромеханике по причине взрывного роста машинного кода, грозящего к тому же полной потерей эффективности и цифровой разрешимости прикладных расчетов.
Главное достоинство алгоритмических языков программирования – это прямое отображение командных предложений на аппаратные средства конкретной ЭВМ, что позволяет целенаправленно оптимизировать наиболее критичные фрагменты программного кода для достижения наибольшей эффективности вычислений.
Функциональный язык. На функциональном языке программирования записываются предложения со строго определенным или уникальным физическим смыслом, исполнение которых всегда оперируют исходными данными с контекстно-зависимым содержанием. Построение такой языковой среды необходимо для прямой записи законов гидромеханики, в форме максимально приближенной к аналитическому представлению прикладной задачи в терминах естественного физико-математического мышления. В простейшем случае представление программной среды может быть выполнено в виде «языковой оболочки» над алгоритмическими исполняющими процедурами.
Вычислительный эксперимент в гидромеханике всегда означает манипулирование большими объемами строго систематизированных числовых данных. Поэтому организация числовых структур должна служить связующим звеном между алгоритмическими «глаголами» и функциональными «определителями». Следовательно, все числовые объекты должны содержать не только текущие расчетные величины, но и информацию об описываемом физическом явлении; ссылки на отсчеты времени и пространственные координаты; а также дополнительные «признаки», задающие допустимые методы трансформации и физической интерпретации числовых данных в любой момент времени проведения вычислительных экспериментов.
По аналогии с термином: «признак» для числовых данных, можно ввести термин: «образец», применяемый к исполняемым процедурам и функциям, связывающим исполняемую процедуру с допустимыми методами ее автоматического использования. Этого достаточно для формирования управляющего языка, где слова служат определителями смысловых или физических терминов, к которым всегда связаны описательные «признаки» и исполнительные «образцы». Формально можно ввести понятие «базы знаний», где использование слов определяется их внутренним смыслом и связями с текущим состоянием языковой или исполнительной среды. Если в качестве аналога пользоваться Русским языком, то суть операций будет связываться не только с местоположением слов внутри предложения, но также доопределяться строгими контекстными расширителями (образцами и признаками) в виде приставок, суффиксов и окончаний.
Двухуровневое расслоение языковой среды позволяет ограничить алгоритмический подход использованием только локальных данных, что необходимо также для обеспечения множественной реентерабельности всех исполняемых модулей в многозадачном режиме, поддерживая управление ходом вычислительного эксперимента и контроль всех числовых массивов на функциональном уровне.
С появлением нового математического инструментария в виде высокоэффективной вычислительной техники, стало снова актуальным проведение естественно-философских и теоретико-лингвистических исследований в приложении к формальным и аппаратным реализациям языков программирования [Уинстон, 1980], как новым средствам экспериментальной физики, математического мышления и искусственного интеллекта. Целью же новых метафизических поисков должно являться не столько открытие новых законов человеческого миропонимания, сколько поиск формализованных вычислительных объектов, правил их трансформации и эффективного использования при решении прикладных задач механики сплошной среды.
Второстепенным направлением поисков при проектировании программных комплексов является отработка методов выделения канонических зависимостей и выверенных законов природы из огромных потоков информации, которыми позволяют оперировать современные информационно-вычислительные и опытно-экспериментальные комплексы, а также телеметрические системы для непосредственных наблюдений за природными явлениями.
Проектирование также представляет собой процесс мышления, оперирующий с особыми квазиязыковыми объектами.
Здесь уместно ввести в рассмотрение характеристику сложности логического объекта, под которой будем понимать степень взаимозависимости компонент. Если физическое явление существует само по себе и не зависит от авторских предпочтений, то назовем это свойство СКАЛЯРНОСТЬЮ логического объекта.
Проект связывает явление с описательной идеей, что нужно понимать как познание явления с помощью обобщающих законов. Проект, основанный на законах, определяет конкретное явление в как бы пространственных координатах, назовем это свойство ВЕКТОРНОСТЬЮ логического построения, а сам объект просто сложным или сложенным из различных компонент.
Использование такого логического построения может быть оторванным от реального физического явления (что справедливо для вычислительных задач), но при этом с помощью начальных и граничных условий явление может быть поставлено в различные логические координаты, в том числе за пределы области определения математической модели. Соответствующее взаимодействие явления с окружающей средой или закритические режимы существования явления будем определять с помощью МАТРИЧНОГО логического объекта, или объекта, составленного из сложения независимых и произведения взаимосвязанных компонент.
Авторская языковая практика никогда не чуждается непротиворечивой троичной логики (трилектики). Если высказывается какая-либо идея, то она оформляется в виде предложения с существительным, глаголом и связывающими их определениями. Для увязки предложения с контекстом записываются поясняющие тезисы, состоящие из ключевой идеи, ее конкретных приложений и сложных правил взаимосвязи обсуждаемых явлений и происходящих с ними процессов. Затем краткий текст расширяется изложением исходных понятий и последствий до уровня приемлемых в практике реализаций, оптимально ориентированных на материализацию исходной идеи.
Применим последние высказывания к внутренним свойствам моделируемых физических явлений. Пусть основа их совместного существования характеризуется понятием: "процесс", который составляется из трех компонент (рис. 2.4):
а) "ИСХОД" - процесс, определяющий зарождение явления;
б) "СУТЬ" - текущее состояние рассматриваемого явления;
в) "РАЗВИТИЕ" - правила взаимодействия с окружающей средой, в том числе определение условий, приводящих к вырождению явления.
Обратим внимание, что характеристика сложности инвертируется, если происходит изменение основания для определения логической значимости определений.
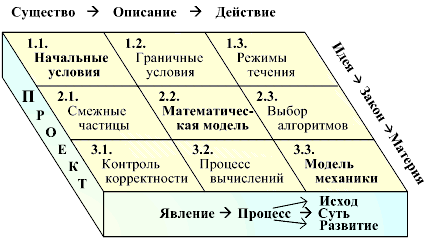
Рис. 2.4. Представление троичной логической матрицы для решения задачи по методу "крупных частиц".
Для иллюстрации рассмотрим проход от идеи к материи на примере процесса построения проекта:
- "Исход" - обладает скалярным смыслом и по сути просто формулирует постановку задачи;
- "Суть" - является пространственной величиной и определяет текущее состояние и направление в сторону развития реализуемого проекта;
- "Развитие" – комплексное или матричное понятие, связывающее новый проект с независимыми компонентами, противоречивыми идеями и реально существующими физическими явлениями
Теперь, когда введены основные предпосылки и законы, описывающие троичную логическую матрицу (рис. 2.4), можно рассмотреть содержание матрицы проекта программы для проведения вычислительного эксперимента.
Каждый столбец матрицы можно представить как пакет процедур, оперирующий с определенным типом машинной информации (X.. - означает перечисление 1+2+3..):
X.1 Процедуры, обеспечивающие доступ к структурам числовых данных, которые пользуются одними и теми же методами доступа к информации. Каждый элемент столбца преобразует числовые данные к виду, удобному для использования на данном этапе вычислений;
X.2 Система функций, исполняющая ведущие алгоритмы математической модели течения жидкости. Если проект программы ориентирован на оперативное (или интерактивное) использование, то эти функции занимают подчиненное положение между процедурами интерпретации данных (Х.1) и управляющими предложениями функциональной (языковой) среды программирования (Х.3);
X.3 Языковая среда управляет процессом проведения вычислительного эксперимента. Сюда входят все информационно - логические операции, обеспечивающие назначение расчетных режимов, обработку особых ситуаций, и выполнение активного диалога с пользователем программы.
Формально, каждая строка матрицы определяет один из расчетных этапов:
1.Х - построение расчетной области и начальных условий;
2.Х - применение математической модели;
3.Х - преобразование результатов вычислений.
В таком случае вдоль строки могут быть установлены только рекурсивные (функциональные) связи между процедурами, реальные действия которых определяются состоянием данных о ходе вычислительного эксперимента. Предложение, активизированное в столбце "действие", приведет к обращению к процедурам смежного столбца "описание", где проанализируются физические параметры течения жидкости и замкнется цепочка исполняющих функций вплоть до самого низкого уровня (столбец "существо"), что приведет к подготовке "описания" для применения конкретных законов гидромеханики и завершению требуемого "действия". Если числовые объекты попадают в зону граничных условий или в критические режимы течения жидкости, то производится непосредственное рекурсивное вхождение в функции столбца "описание" для предварительной инициации экстраполированных или специальных эмпирических данных, использование которые не повлияет на формализованные операции столба процедур "описание".
Процедуры, составляющие столбцы матрицы, трактуются как неизменные алгоритмы, преобразующие числовую информацию. В практическом программировании элементы столбца могут быть включены в проблемно ориентированный пакет программ, где каждая процедура разработана и отлажена как отдельный подпроект, который затем включен в систематизированную библиотеку или "базу знаний" вычислительного эксперимента в целом. Эта часть программного комплекса может эффективно строиться с помощью современных объектно-ориентированных языков программирования типа С++.
Линии логической матрицы образуют описание существа физического явления, а столбцы составляют исполняемые пакеты вычислительных операций в строгом соответствии с принятыми для моделирования физическими законами. Эти логические направления не имеют прямой алгоритмической связи, подобно существительным и глаголам в предложениях естественного языка, чем и достигается независимость и непротиворечивость разработки проектных решений при создании сложных программных комплексов.
Если в определениях законом будут использованы пакеты программ, созданные с использованием декларативных методов программирования, то вдоль строк должны выстраиваться динамические процедуры контекстно управляемого функционального метода программирования, нацеленные на интерпретацию и глубокий анализ текущих режимов гидродинамического моделирования, и автоматически управляющие ходов вычислительного эксперимента в определениях искусственного интеллекта.
При последовательном переборе элементов матрицы получается словесное описание программы: на основании начальных и граничных условий назначается режим течения жидкости. Затем анализируются локальные свойства крупной частицы жидкости, и на основании этого анализа выбирается математическая модель преобразования расчетной области. На завершающем этапе контролируется корректность выполненных расчетов и расчетная область подготавливается к повторению вычислений. Многократное исполнение матрицы - программы образует процесс, моделирующий течение жидкости во времени.
Пока логическая матрица введена чисто формально. При описании ее элементов можно воспользоваться расширенной терминологией: "идея проекта"; "описание явления", что означает выбор соответствующего элемента матрицы. В отношении программных проектов удобнее пользоваться термином "реализация" вместо "материя", тогда получится расширение: "существо реализации" или "результирующее действие" и т.п.
Рассмотрим основные операции, которые применимы к элементам матрицы. Эти операции могут быть разделены по степени сложности или взаимозависимости оперируемых объектов:
1. Скалярные или логические операции, суть которых состоит в выборе или отсеивании компонент включаемых в троичную матрицу.
Например: на первом проходе, от "идеи" к "материи", используется операция логического сложения для выявления новых результатов в реализации проекта; второй проход, от "материи" к "идее", позволяет с помощью операции логического произведения (сопоставления) отсеять лишние идейные предпосылки;
2. Пространственные, или операции типа сложения (усложнения), применяются для комплексного описания выполняемых работ. Сложение допустимо для элементов, находящихся в одном логическом базисе, в нашем случае это столбец или строка троичной матрицы.
Складываемые элементы должны иметь связанную терминологию и опираться на сопоставимые смысловые правила. При этом сами элементы не могут быть объединены в одно понятие, так как по определению компоненты одного базиса должны быть независимы (=направления базиса ортогональны). Примерами операции сложения служат отмеченные абзацы данной статьи, в которых строятся логически связанные определения из трех различных понятий;
3. Матричная операция произведение (умножение) применяется (как и положено для векторов в тензорной алгебре) к элементам, измеренным относительно разных базисов, но одинаковых по смысловому содержанию. Наиболее важной характеристикой тензора является определитель, который задает геометрический объем базиса. В случае нашей троичной матрицы, необходимо обеспечить возможность построения определителя на логическом уровне, то есть элементы матрицы, включаемые в операцию умножения при вычислении определителя, должны быть совместимыми по смыслу. Личный опыт автора показывает, что соблюдение последнего условия обязательно для сохранения непротиворечивости самой матрицы.
Если задача достаточно проста, или проект не предусматривает комплексного решения, то матрица может быть существенно упрощена.
Пусть, к примеру, останется только главная часть проекта, выраженная диагональными элементами троичной матрицы (рис. 2.4): "Начальные условия"; "Математическая модель"; "Модель механики ‑ в виде представления результатов расчета". По аналогии с тензорной алгеброй, можно сказать, что проект определен в ортогональном глобальном базисе и составлен из независимых (в дифференциальном смысле) компонент. В этом случае легко поменять местами элементы 1.1 и 3.3, что приведет к формулированию обратной задачи. В случае полной матрицы, обращение уже не будет столь тривиальным, но, тем не менее, не теряет смысла переформирование матрицы, оглядываясь на связи между компонентами в соответствии с алгебраическими законами (правилом Саррюса).
Затем, если необходимо использовать числовые данные, сформированные в виде функциональных структур, например, с помощью базы данных, то можно рассмотреть троичную матрицу в транспонированном виде. В этом случае, при проектировании и логическом построении вычислительного эксперимента, в описание физического явления должны включаться специальные линейные алгоритмы и процедуры, обслуживаемые транзакциями для доступа к базам исходных данных. Аналогичная задача встает при создании программ для обработки и анализа больших объемов числовых данных, получаемых в результате проведения физического эксперимента.
Завершая раздел исходных логических предпосылок, покажем троичную связь между всеми объектами и процессами при проведении вычислительного эксперимента в гидромеханике:
1. База знаний ‑ скалярное (линейное) представление всех исполнительных процедур, которые реализуют математические операции наиболее эффективным способом;
2. Алгоритмический объектно-ориентированный пакет процедур – как векторная систематизация исходных данных и результатов расчета, дающая полное описание физического явления и вводящая однозначные правила трансформации и смысловой интерпретации этих данных;
3. Искусственный интеллект – как матричная или функциональная организация всех управляющих предложений, которые на языковом уровне управляют процессами подготовки, проведения и представления результатов прикладных вычислительных экспериментов в гидромеханике.
Для иллюстрации особенностей среды программирования воспользуемся базовыми конструкциями языка С++, обладающего наилучшими способностями к прямому отображению аппаратных особенностей цифровых ЭВМ, и в то же время имеющего мощные препроцессорные средства для обобщения вычислительных операций и расширения функциональных возможностей как самого языка, так и его объектно-ориентированной среды, что обеспечивает проведение разработок программных комплексов любой сложности.
Так, к примеру, для придания числовым величинам необходимых функциональных признаков, элементарные переменные могут быть заменены структурированными объектами, типа:
typedef struct { char s; int d } integer; // для индексов,
typedef struct { char s; double d } real; // для чисел,
где символ s служит управляющим определителем при соответствующей числовой величине, и используется в качестве предиката при выборе допустимых операций на этапе выполнения программы.
Язык программирования С++ представляется с помощью полноценного классического компилятора, а потому динамическое (т.е. в ходе выполнения программы) управление внутренним содержанием исполняемых процедур и функций принципиально невозможно. Однако на этапах компиляции в качестве упоминаемых выше образцов могут выступать невидимые для разработчика расширители имен процедур, формируемые из списков используемых параметров. Показанные языковые механизмы означают, что С++ обладает богатыми функциональными возможностями на этапе компиляции новых программ, обеспечивая генерацию статического и довольно громоздкого машинного кода.
Для описания физико-механических свойств течения жидкости, на уровне компилятора должны быть построены три типа элементарных вычислительных объекта.
1. Скалярные числовые данные, которые служат для задания инвариантных характеристик течения, как например:
real T; // отсчет времени от начала вычислительного эксперимента,
real t; // шаг во времени для моделирования нестационарных процессов.
2. Векторные величины определяют точку в пространстве (рис. 2.5):
typedef struct { char s; double X,Y,Z } Point; // координатная точка в общей системе отсчета
typedef struct { char s; double x,y,z } point; // координатный отсчет внутри элементарной частицы жидкости
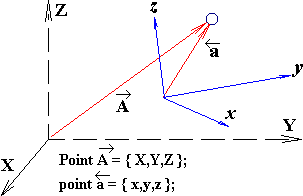
Рис. 2.5. Программное и пространственное представление вектора точки.
3. Элементарная (крупная) частица жидкости имеет малые, но конечные пространственные размеры (рис. 2.6), и может быть определена с помощью компьютерного объекта – тензора:
typedef struct { char s; point X,Y,Z } cell; // координатная ячейка элементарной частицы жидкости.
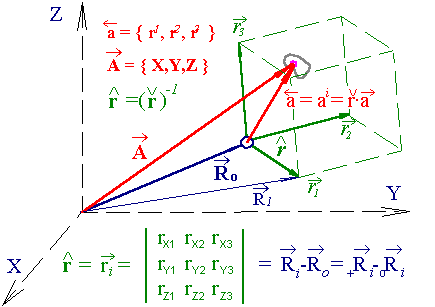
Point R = { X, Y, Z }; cell r = { { X.x, X.y, X.z } ,
{ Y.x, Y.y, Y.z } ,
{ Z.x, Z.y, Z.z } };
Рис. 2.6. Программное и пространственное представление элементарной частицы жидкости.
Предметом тензорных вычислительных операций является тетраэдр базисных векторов (рис. 2.6), связывающих пространственный параллелепипед элементарного числового объекта, внутри которого все кинематические параметры течения и свойства жидкости изменяются строго по линейным законам. Гидродинамические расчеты в таком параллелепипеде сводятся к линейным интерполяционным процедурам, при которых исходные локальные базисы образованы простыми единичными векторами.
В случае же свободных границ, и особенно – подвижных, а также на нерегуляризованной расчетной сетке, тензорные определения элементарных частиц становятся недоопределенными или вырожденными, что требует применения экстраполяционных расчетов граничных условий, обладающих более высоким порядком разностного дифференцирования, и которые могут быть реализованы исключительно путем применения функциональных методов программирования, нередко поднимающихся до уровня языковой среды искусственного интеллекта.
В приведенном определении тензора формы элементарной частицы жидкости использованы три базисных вектора, каждый из которых имеет собственные предикаты-признаки, однозначно определяющие как собственные пространственные привязки, так и физические особенности этих векторов. Это необходимо для автоматизации проектирования и построения прикладных вычислительных экспериментов, позволяя на языке высокого уровня определять только основные законы гидромеханики, а согласование координатных систем и физических размерностей будет выполняться автоматически частично при компиляции программных модулей, и в процессе контроля расчетов на этапах проведения вычислительного эксперимента.
Отметим также, что использованные в декларациях на языке С++ прописные буквы для абсолютных отсчетов (длинных векторов) и строчные – для локальных систем координат (внутренних отсчетов) приняты условно, т.к. в процессе исполнения программы система отсчета для конкретных числовых объектов, векторов или тензоров может изменяться, а потому их текущее состояние можно определить только с помощью признаков (s – предикатов) непосредственно на этапах исполнения программы.
С помощью «признаков» функциональные особенности среды для моделирования течений жидкости могут быть перенесены также и на этапы исполнения программы. Пусть каждый числовой объект сопровождается следующими s – предикатами, образованными простыми битовыми масками:
3 бита – характеристика числового объекта:
“000” – безразмерный скаляр или инвариантная величина;
“001” – вектор в абсолютной системе координат;
“010” – короткий вектор в локальном базисе частицы жидкости;
“011” – размерная скалярная величина, например – время;
“100” – тензор формы жидкой частицы в глобальном базисе;
“111” – определение тензорной величины в локальном базисе;
“101” – смешанный базис проекций векторов на локальную СК;
“110” – базис локальных векторов в проекциях глобальной СК.
Оставшиеся 5, 13 или более бит могут быть использованы для характеристики текущего состояния смежных частиц жидкости, например, для контроля готовности к интерполяционным пересчетам на этапах согласования конвективных свойств и условий сохранения, или при необходимости динамического перехода к экстраполяционным процедурам на свободных границах и в зонах вырождения численных решений.
Постоянный контроль аналогичных битовых масок-признаков особенно важен в случае глубокого распараллеливания вычислительных операций на многопроцессорных ЭВМ.
Все вычислительные объекты должны создаваться либо при начальной подготовке исходных гидродинамических полей, либо конструироваться в ходе вычислительного эксперимента с помощью специальных логических процедур, способных на функциональном уровне контролировать особые режимы течения жидкости и управлять ходом проведения вычислительного эксперимента. Новые объекты не могут порождаться или уничтожаться в результате математических действий, моделирующих базовые законы гидромеханики.
К основным действиям по моделированию внутренней динамики жидких частиц относится математическая операция ‑ произведение, которая в тензорных определениях применима к векторным величинам при условии, что все компоненты сомножителей измерены в дуально противоположных базисах. Формально это означает запрет повышения ранга тензорных величин с помощью операции умножения. Все операции умножения должны носить исключительно интерполяционный характер, суть которого состоит в линейном перераспределении характеристик течения между смежными элементарными частицами жидкости.
В тензорной форме динамика несвободной частицы жидкости будет определяться с помощью векторного аналога закона Ньютона:
Fi = Wj ·M ji или
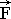 =
= 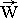 ·
· 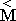 , который означает, что внешняя сила
, который означает, что внешняя сила
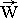 , действующая на выделенную из потока крупную частицу жидкости
, действующая на выделенную из потока крупную частицу жидкости 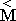 , вызывает реакцию
, вызывает реакцию
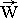 , величина и направление которой зависит как от внутреннего состояния (инерции) этой частицы, так и от ее способности деформироваться, поглощать или усиливать внешние проявления энергии движения. Жидкая частица будет двигаться в соответствии с традиционным законом Ньютона для точки со скалярной массой только в том случае, если ее освободить от связей с окружающей сплошной средой.
, величина и направление которой зависит как от внутреннего состояния (инерции) этой частицы, так и от ее способности деформироваться, поглощать или усиливать внешние проявления энергии движения. Жидкая частица будет двигаться в соответствии с традиционным законом Ньютона для точки со скалярной массой только в том случае, если ее освободить от связей с окружающей сплошной средой.
Связывая тензор массы с формой частицы жидкости 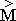 =
=  ·
·
 , получим определение плотности или внутренней энергии, которая в общем случае придает жидкой среде анизотропные свойства:
, получим определение плотности или внутренней энергии, которая в общем случае придает жидкой среде анизотропные свойства:
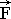 = rik · r kj
·
= rik · r kj
· 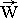 =
=  ·
·  ·
· 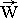 ,
где:
,
где:  – тензор формы крупной частицы жидкости;
– тензор формы крупной частицы жидкости;
 – тензор плотности, характеризующий внутреннее состояние частицы жидкости, условно понимаемый как оператор, учитывающий силовое взаимодействие малого расчетного элемента с окружающей сплошной средой.
– тензор плотности, характеризующий внутреннее состояние частицы жидкости, условно понимаемый как оператор, учитывающий силовое взаимодействие малого расчетного элемента с окружающей сплошной средой.
По сути введенных понятий и условных обозначений вполне достаточно для построения прикладных вычислительных экспериментов в гидромеханике. Кратко декларируем эти обозначения:
Прописными буквами обозначаются величины, измеренные относительно центра единой абсолютной системы координат;
Строчными буквами – в локальном базисе, связанном с конкретной крупной частицей жидкости.
Тогда:
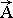 = Ai – пространственная точка (вектор), измеренная и отмеченная в глобальной системе координат [м];
= Ai – пространственная точка (вектор), измеренная и отмеченная в глобальной системе координат [м];
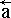 = ak – векторный отсчет внутри локального базиса элементарной частицы жидкости [м-2];
= ak – векторный отсчет внутри локального базиса элементарной частицы жидкости [м-2];
 =
= 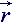 k = rik –тензор формы крупной частицы жидкости [м3];
k = rik –тензор формы крупной частицы жидкости [м3];
 =
= 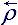 j = r kj – тензор плотности [кг·м-3];
j = r kj – тензор плотности [кг·м-3];
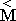 = M ij =
= M ij =  ·
·  – смешанный тензор, соотносящий внутреннее состояние частицы на абсолютную систему отсчета [кг];
– смешанный тензор, соотносящий внутреннее состояние частицы на абсолютную систему отсчета [кг];
Вычислительный эксперимент в гидромеханике обобщенно можно представить как процесс трансформации поля скорости во времени:
+ =
=  +
+ 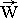 ·t, где:
t – малый расчетный интервал времени.
·t, где:
t – малый расчетный интервал времени.
Уточнение нового поля скорости + является вторым шагом дифференцирования первого порядка, завершающего исполнение закона Ньютона для уравновешивания внешних сил соответствующими приращениями скорости свободного движения частиц жидкости.
является вторым шагом дифференцирования первого порядка, завершающего исполнение закона Ньютона для уравновешивания внешних сил соответствующими приращениями скорости свободного движения частиц жидкости.
Построение вычислительного эксперимента именно таким образом, чтобы все операции сводились не более чем к разностному дифференцированию первого порядка, является главной особенностью лагранже-эйлерова подхода при численном решении задач гидромеханики. Иначе этот подход можно назвать методом расщепления решения по физическим процессам, который может быть сформирован тремя условными этапами численного решения прикладной задачи:
1 этап. По текущему полю скорости уточняется состояние крупных частиц жидкости на следующий момент времени:
+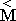 =
=  · (
· (  +
+  · t ),
· t ),
где:  · – тензор отображения текущего поля скорости на локальный базис крупной частицы;
· – тензор отображения текущего поля скорости на локальный базис крупной частицы;
 – тензор внутреннего состояния жидкой частицы на текущий момент времени.
– тензор внутреннего состояния жидкой частицы на текущий момент времени.
2 этап. После уточнения результирующего вектора всех внешних сил, воздействующих на крупную частицу жидкости, производится расчет нового поля скорости:
+ =
=  +
+ 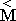 -1·
-1·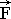 ·t.
·t.
В данном выражении тензор массы оказывается в знаменателе, что позволяет его идентифицировать как условную гидродинамическую особенность, оказывающую влияние на течение жидкости, при этом в случае модели идеальной жидкости такое влияние будет распространяться не только на смежные частицы, но и на весь поток жидкости в целом.
3 этап. В результате выполнения первых двух этапов произойдет пространственное смещение всех крупных частиц жидкости, а новые гидродинамические поля отчасти перестанут удовлетворять условиям неразрывности и изотропности исходной среды. В зависимости от типа задачи, на заключительном этапе необходимо вносить релаксационные поправки к внутренним свойствам и условиям взаимодействия между частицами жидкости, а также проводить сквозной контроль качества решения и, при необходимости, применять схемы для адаптации или эмпирической подмены решений в зонах, где вычислительная модель дает заведомо неверные результаты.
Так, например, для получения тензора конвективных скоростей, входящего в уравнение движения на неподвижной сетке по Эйлеру, достаточно произвести нормировку тензора локальных скоростей:
(  +
+  ·t )·
·t )·  -1 = 1 +
-1 = 1 +
 ·t,после чего он станет независимым от собственного локального базиса и позволит обобщить поле скорости на ближайшие или смежные частицы жидкости и, в процессе обратной интерполяции восстановить тензор плотности
·t,после чего он станет независимым от собственного локального базиса и позволит обобщить поле скорости на ближайшие или смежные частицы жидкости и, в процессе обратной интерполяции восстановить тензор плотности
 к исходному виду, либо аккумулировать в нем условную внутреннюю энергию и дополнительные напряжения, возникающие за счет вязкости, сжимаемости и упругости в сплошной среде:
+
к исходному виду, либо аккумулировать в нем условную внутреннюю энергию и дополнительные напряжения, возникающие за счет вязкости, сжимаемости и упругости в сплошной среде:
+ =
=  +
+  ·t,где:
·t,где:
 , в пересчете на смежные частицы, будет определять действующие извне силы.
, в пересчете на смежные частицы, будет определять действующие извне силы.
Граничные условия и критические режимы течения, независимо от методов постановки вычислительного эксперимента, всегда отмечаются недостатком информации для интерполяционного перестроения характеристик частиц и смежных полей жидкости. В этом случае используются специальные алгоритмы для асимптотических или эмпирических упрощений, и численных методов экстраполяции расчетных параметров на недостающие грани жидкой частицы. Выбор и исполнение таких алгоритмов может происходить только на уровне функционального языка программирования, обеспечивающего контроль численных расчетов и управление вычислительным экспериментом в целом.
При использовании криволинейных систем координат, есть возможность наиболее качественного и повсеместного согласования пространственных аппроксимационных критериев, что фактически будет означать сведение всех уравнений механики к каноническому виду, обеспечивающему, к тому же, автоматическое выполнение граничных условий, и в том числе на открытых границах расчетной области. Обеспечение столь жестких условий пространственной аппроксимации для построения вычислительных моделей в механике сплошных сред будет означать фактическое решение задачи чисто аналитическими методами, и потому возможно только в случае идеальных или искусственно подобранных расчетных областях.
В прикладных же задачах, решаемых в произвольных или сложных геометрических и физических условиях, построение криволинейных и ортогональных сеточных областей становится невозможным. При частичном решении такой геометрической задачи, она сводится к использованию косоугольных ячеек на нерегуляризованных узлах, что не дает никаких ‑ ни теоретических, ни вычислительных преимуществ по сравнению с обычными прямоугольными эйлеровыми координатными сетками, которые, при необходимости, могут иметь переменный шаг или становиться нерегуляризованными.
Для полной реализации лагранже-эйлерова подхода нет необходимости построения криволинейных координатных сеток, так как деформационные характеристики гидродинамических полей полностью учитываются внутренними энергетическими характеристиками элементарных частиц жидкости, исходная форма которых на каждом такте вычислений по времени может сводиться к обычным прямоугольным эйлеровым сеточном ячейкам.
Важным преимуществом прямоугольных расчетных сеток является то обстоятельство, что, по крайней мере, на одном из этапов гидродинамических расчетов, форма элементарных частиц жидкости будет представляться ортогональными или даже диагональными тензорами II-го ранга, что значительно упростит форму представления законов механики, и исключит недостаточную обусловленность вычислительных операций из-за сильных начальных деформаций сеточных ячеек (рис. 2.7).
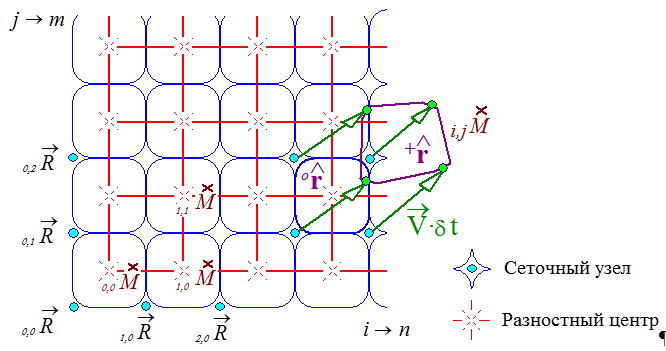
Рис. 2.7. Прямоугольная регуляризованная сеточная область.
Правые тензорные индексы используются для отметки пространственных компонент, характеризующих внутренние свойства элементарных числовых объектов в связанной с ними локальной системе координат:
 =
=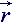 k = rik .
k = rik .
Левыми нижними индексами будем отмечать местоположение этой частицы в абсолютном пространстве по номерам расчетных узлов:
ij =
=  ( iX, jY ),где локальный базис ij
( iX, jY ),где локальный базис ij связывается с координатами X=i·x, Y=i·y.
связывается с координатами X=i·x, Y=i·y.
Тогда левый верхний индекс можно использовать для отметки расчетных шагов во времени:
k =
=  ( 0T+k·t );
( 0T+k·t );
+ = k+1
= k+1 .
.
Иногда, для упрощения записи, индексными отметками: минус "‑" и плюс "+", будем отмечать смежные в пространстве ячейки или предыдущий и последующий расчетные шаги во времени, соответственно:
++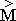 = i+1,j+1k+1
= i+1,j+1k+1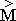 .
.
Построение прямых вычислительных экспериментов в гидромеханике может быть основано на непротиворечивом проектировании интерполяционных процессов в пространстве и во времени, при которых на каждом такте вычислений будет происходить согласование моделируемых законов механики, поочередно относимых к границам элементарных расчетных ячеек (Эйлеров этап) и к образуемым этими ячейками крупным частицам жидкости, участвующим как бы в свободном движении с внутренними деформациями (Лагранжев этап).
Главными особенностями таких интерполяционных операций, формально образующих привычное разностное дифференцирование физических полей для моделирования гидродинамических процессов на сеточных расчетных областях являются:
1 – результат разностного дифференцирования первого порядка всегда смещается в пространстве с узлов расчетной области, в которых определены исходные значения параметров пространственного поля, на центры масс условных расчетных ячеек, ограниченных этими узлами. Если разностное дифференцирование второго (четного) порядка не тривиально, то ему также присуще аналогичное, но меньшее смещение результирующей точки (рис.2.7).
2 – при прямом моделировании нестационарных течений все приращения характеристик течения во времени необходимо относить на смещенные в пространстве ячейки жидкости. Такие смещения всегда соизмеримы с размерами расчетных ячеек и потому в инженерных приложениях не могут быть ни названы малыми, ни проигнорированы.
3 – в явной или неявной форме разностные расчетные схемы первого порядка для аппроксимации гидродинамических полей самоцентрируются. Достижение корректности и надежности вычислительных экспериментов возможно только при изначальном управлении процессами такого центрирования, направленного на приведение вычислительных операций к схемам «прогноза и коррекции», что особенно важно при построении граничных условий и в случае динамического внесения внешних возмущений в исполняемую вычислительную модель.
Вычисления значительно усложняются вблизи открытых и жестких границ, а также в зонах нарушения режимов течения, связанных с образованием кавитационных разрывов, свободных поверхностей и вихревых нитей.
Этапы вычислений с использованием неподвижных (Эйлеровых) пространственных сеток могут быть определены следующим образом:
‑ На первом этапе ведется построение тензора внутренних характеристик для всех расчетных ячеек в соответствии с текущим состоянием пространственных полей. Определяются новые кинематические параметры для этих ячеек, таких как приращение скорости для ячейки – частицы в целом, изменение скорости ее деформации (если жидкость идеальная, то исходная скорость деформации отсутствует).
‑ На втором этапе, после пространственного смещения всех частиц, производится перерасчет исходных гидродинамических и физических полей, и повторным интегрированием разностных уравнений завершается моделирование движения сплошной среды.
‑ На третьем этапе осуществляются все необходимые расчеты для обеспечения режима «коррекции» и центрирования расчетных шаблонов, образующих обобщенный подход численного метода «прогноза и коррекции». В реальности же здесь решается задача согласования заданных физических свойств течения жидкости, и выполнения других особых условий проведения вычислительного эксперимента.
В частности, при решении задач гиперболического типа, к которым относится моделирование длинноволновых процессов в океане, третий этап практически полностью исключается за счет предварительного аналитического подбора весовых коэффициентов систем дифференциальных уравнений, а именно – заданием фазовой скорости[3]
распространения волн: С=Ögh. Но даже для столь простого вычислительного эксперимента на согласующем этапе расчетов остается сложнейшая проблема качественного согласования граничных условий. Это объясняется еще и тем, что на втором этапе вычислений из интерполяционных процедур выпадают все граничные точки: 0,j и i,0
и i,0 и на противоположных границах. В общем случае восстановление расчетных величин на границах возможно путем экстраполяции решений из внутренней области, что реализуемо только при условии отсутствия гидродинамических особенностей вблизи границ и гладкости внутренних гидродинамических полей.
и на противоположных границах. В общем случае восстановление расчетных величин на границах возможно путем экстраполяции решений из внутренней области, что реализуемо только при условии отсутствия гидродинамических особенностей вблизи границ и гладкости внутренних гидродинамических полей.
Любые гидродинамические расчеты сводятся к аппроксимации монотонно изменяющихся физических параметров течения жидкости на дискретных узлах расчетной сетки. В задаче о распространении длинных волн в океане и в его прибрежной зоне возможно точное аналитическое предсказание характерных масштабов исходных гидродинамических процессов. В результате аналитического решения для скорости распространения длинных гравитационных волн С=Ö(gh) и дисперсионным условием, не допускающим зарождение волн с периодом меньше исходного, сеточная область может быть адаптирована под минимальную длину моделируемых волн, с более частой сеткой вблизи берегов и многократно увеличенной на больших глубинах открытого моря.
Такая адаптация сеточной области позволит многократно уменьшить объемы используемой оперативной памяти и значительно повысить общую скорость вычислений. Но в этом случае невозможно использовать простые циклические алгоритмы для расчетов на регуляризованных сетках, так как все разорванные узлы становятся подобны свободным границам, на которых для восстановления величин в разорванных узлах необходимо активно использовать экстраполяционные методы.
Если предварительное определение параметров расчетной области невозможно, то для построения эффективных вычислительных экспериментов необходимо непрерывно оценивать интенсивность потоков в узлах расчетной сетки и внутренние напряжения в элементарных частицах жидкости, дробя или сливая расчетные ячейки в соответствии с особыми пространственными критериями.
В программной реализации динамическая адаптация расчетной сетки может выполняться рекурсивными методами, например, по критериям превышения кривизны характеристик пространственных полей, или при необходимости замедления расчетного шага в конкретной ячейке по критериям устойчивости численного решения.
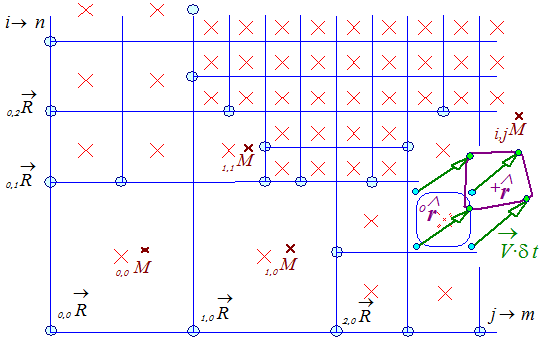
Рис. 2.8. Прямоугольная нерегуляризованная сеточная область.
На рисунке 2.8 показано, что при использовании нерегуляризованных сеток внутренние разрывы появляются непредсказуемо и почти хаотично. Тем не менее, в инженерных приложениях только неравномерные сетки позволяют повсеместно удовлетворить аппроксимационные критерии и минимизировать негативное влияние чисто сеточных эффектов, связанных с проявлением неконтролируемой вязкости, упругости и сжимаемости жидкости. В информационном же плане решение задачи превращается в непрерывное исследование ближайшего окружения всех крупных частиц жидкости, сводящееся к экстраполяционному восстановлению физических параметров жидкости как в динамически формируемых частицах жидкости, так и в разорванных узлах сеточной области.
В таком случае построение вычислительного эксперимента может опираться только на функциональные методы программирования, с глубоким использованием поисковых алгоритмов и рекурсивно подстраивающихся под свойства течения процедур, способных обеспечить уточненные гидродинамические расчеты как в областях с наибольшей интенсивностью деформации на внутренних фронтах свободных течений, так и в локальных зонах с повышенной концентрацией энергии вблизи особых гидродинамических точек.
[1] Папп Александрийский (Pappus, 2-я пол. III в.) – математик и механик эпохи позднего эллинизма, автор сочинения "Synagoge" ([Математическое] собрание).
[2] Вступительные фразы из предисловия Исаака Ньютона к первому изданию «Математических начал натуральной философии» [1936], с. 1.
[3] Из волнового соотношения величина фазы определяется как i(kx-wt) а фазовая скорость волны: V=w/k. Если эта скорость зависит от длины волны, то групповая скорость пакета волн, как реальная скорость распространения волновой энергии может быть оценена как: U = dw / dk = V -l·dV/dl. Так если для волн Герстнера V = sqrt( g·l /2/p ), то U=0,5·V; для капиллярных волн: V = sqrt( T·2·p / r / l ) и - U=1,5·V.
 Формально, на разделенных во времени этапах вычислительного эксперимента в механике сплошных сред, может быть введен своеобразный векторный аналог Закона Ньютона, определенного с помощью тензорной операции умножения, где внешняя сила F задается в абсолютной системе координат, а реакция W – уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы M будет не только аккумулировать энергию поступательного движения, но также определит инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
Формально, на разделенных во времени этапах вычислительного эксперимента в механике сплошных сред, может быть введен своеобразный векторный аналог Закона Ньютона, определенного с помощью тензорной операции умножения, где внешняя сила F задается в абсолютной системе координат, а реакция W – уже в локальном базисе, вмороженном в элементарную деформируемую частицу жидкости. В этом случае масса жидкой частицы M будет не только аккумулировать энергию поступательного движения, но также определит инерционные свойства деформационного и вращательного движения жидкости в пределах этой элементарной частицы жидкости.
 -1} может быть представлена в виде условного параллелепипеда (в обратной задаче - эллипсоида), внутреннее состояние которого формализуется линейными или обратными
распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных локальных базисов в форме трехмерных тензоров II ранга, задающих линейное (или обратное) распределение внутренних свойств течения между жидкими частицами, однозначно определяемых интерполяционными (без экстраполяции) зависимостями между исходными узлами расчетной области.
-1} может быть представлена в виде условного параллелепипеда (в обратной задаче - эллипсоида), внутреннее состояние которого формализуется линейными или обратными
распределениями скалярных и векторных полей, жестко связанных геометрическими свойствами собственных локальных базисов в форме трехмерных тензоров II ранга, задающих линейное (или обратное) распределение внутренних свойств течения между жидкими частицами, однозначно определяемых интерполяционными (без экстраполяции) зависимостями между исходными узлами расчетной области.


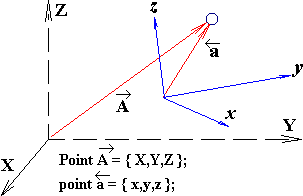

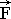 =
= 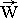 ·
· 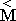 ,
, 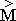 =
=  ·
·
 , получим определение плотности или внутренней энергии, которая в общем случае придает жидкой среде анизотропные свойства:
, получим определение плотности или внутренней энергии, которая в общем случае придает жидкой среде анизотропные свойства: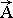 = Ai – пространственная точка (вектор), измеренная и отмеченная в глобальной системе координат [м];
= Ai – пространственная точка (вектор), измеренная и отмеченная в глобальной системе координат [м];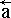 = ak – векторный отсчет внутри локального базиса элементарной частицы жидкости [м-2];
= ak – векторный отсчет внутри локального базиса элементарной частицы жидкости [м-2];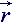 k = rik –тензор формы крупной частицы жидкости [м3];
k = rik –тензор формы крупной частицы жидкости [м3];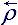 j = r kj – тензор плотности [кг·м-3];
j = r kj – тензор плотности [кг·м-3]; =
=  · t ),
· t ), ·t,
·t, ·t,
·t,
