Дальневосточное отделение
Трехмерная тензорная математика
вычислительных экспериментов в гидромеханике
Вычислительный эксперимент и использование тензорной арифметики
для описания свойств жидкости
Владивосток
ДВО РАН
2005
Трехмерная тензорная математика представляется в виде аналитического обобщения численных решений прикладных задач гидромеханики, основанных на конечноразностных моделях метода крупных частиц (конечного объема). Ориентация изложения на прямые вычислительные эксперименты приводит к поиску элементарных объектов гидромеханики, допускающих сквозную смысловую интерпретацию динамики движения и физических свойств моделируемой жидкости. Рассмотрены особенности непротиворечивого проектирования алгоритмов, сводящиеся к ключевым элементам функционального языка программирования, способного автоматизировать применение тензорных выражений для построения вычислительных экспериментов при моделировании течений жидкости.
Небольшой исторический экскурс, приведенный в первой части книги, адресован читателям, познающим развитие естественных наук во взаимосвязи со становлением прикладной математики. Логические заключения второй части книги заинтересуют разработчиков аппаратных и языковых средств специализированной вычислительной техники. Вычислительные эксперименты гидромеханики представлены в третьей части книги, в которой строгость математических законов по возможности смягчается метафизическими ассоциациями из междисциплинарных естественнонаучных дисциплин.
Книга ориентирована на студентов и инженеров, ведущих поисковые исследования и реализующих прикладные вычислительные эксперименты в различных областях науки и техники, и прежде всего в механике сплошных сред.
Ключевые слова: Математика, тензорный анализ, вычислительный эксперимент, механика, гидромеханика, непротиворечивое проектирование, функциональное программирование, трилектика.
Ответственный редактор: д.г.н. Р.П. Бернгардт
Рецензенты: д.ф.-м.н. В.В. Иванов, к.т.н. С.Д. Чижиумов
© ДВО РАН, 2005
Применение вычислительных экспериментов на основе хорошо разработанной теории, позволяет получать значительные практические результаты. Но вычислительный эксперимент проводится не над реальным объектом, а над его математической моделью, где экспериментальной установкой служит программно-компьютерная система.
Традиционные модели гидромеханики в своей основе имеют системы дифференциальных уравнений в частных производных. Для их анализа эффективно используются конечноразностные методы, среди которых широко распространен метод конечных объемов. Однако исследования многих динамических процессов, например, связанных с сильно изменяющимися границами жидкости, до настоящего времени существенно затруднены (как с точки зрения построения расчетных алгоритмов, так и в плане вычислительных затрат). В этом и состоит актуальность проблемы. Имеющиеся математические приемы зачастую столь громоздки, что за ними легко теряется физика явления. В результате часто возникает проблема потери устойчивости вычислительного процесса. Упрощающие же допущения часто приводят к потере интересных решений.
Одна из причин такого положения раскрывается в первой части данной работы. Она связана с историей развития вычислительных средств и математических моделей, и заключается в опосредованном переходе от физической модели к конечно-разностной – через дифференциальную постановку. В связи с этим в работе ставится цель построения непосредственной конечно-разностной модели механики сплошной среды, основанной на тензорной алгебре. Для этого автором предлагаются расширенные тензорные представления гидромеханики, на основе которых получены численные модели, допускающие использование смешанного подхода Эйлера-Лагранжа, адаптивных алгоритмов и параллельных вычислений. Исследования первой части монографии опираются на исторический обзор и философский анализ развития механики сплошной среды. Этот раздел будет интересен не только специалистам, но также студентам и молодым ученым.
Во второй части работы рассматриваются общие вопросы компьютерной реализации вычислительной гидромеханики. Здесь объявляется принцип сквозной физической интерпретации всех вычислительных объектов и процедур, выполняемых в вычислительном эксперименте. Большое внимание уделяется выбору языка программирования с целью обеспечения поисковых алгоритмов и рекурсивно подстраивающихся под свойства течения процедур, способных обеспечить адаптивное перестроение пространственных сеток.
В третьей, основной части монографии в тензорной форме представлены основы моделирования и алгоритмы решения задач гидромеханики. Выполнена геометрическая формализация движения сплошной среды на основе скалярных, векторных и тензорных числовых объектов. Установлены соответствия свойств введенных тензоров и тензорных операций с реологическими параметрами частиц сплошной среды и моделями течений. Рассмотрев в общей тензорной форме алгоритм моделирования нестационарного течения, основанный на смешанном подходе Эйлера-Лагранжа. Математические модели доведены до простых арифметических выражений с матрицами тензоров. Отмечается возможность распараллеливания процесса вычислений вплоть до каждого конечного объема жидкости.
Последняя часть монографии представляет некоторые примеры реализации численных моделей. Следует, однако, отметить, что результаты расчетов пока сильно ограничены и недостаточно пояснены.
Новизна проведенных исследований и полученных результатов заключается в создании обобщенного тензорного представления задач гидромеханики, позволяющего строить эффективные алгоритмы численного моделирования течений. Монография представляет интерес для молодых ученых и научных работников, занимающихся проблемами численного моделирования в области гидромеханики.
Издание работы рекомендуется также в связи с тем, что в мире стремительно развиваются методы и средства компьютерного моделирования и эксперимента в механике жидкости. Вместе с тем в отечественной литературе явно недостаточно работ, посвященных современной вычислительной гидромеханике, особенно в прикладных задачах, связанных с анализом и проектированием судов, гидротехнических сооружений и других водных объектов.
Доцент кафедры кораблестроения КнАГТУ, к.т.н., С.Д. Чижиумов
Содержание Часть 1. Часть 2. Часть 3. Часть 4. Заключение.
Научное творчество, особенно если таковое связано с изучением естественнонаучных вопросов или с инженерно-техническими исследованиями, не может не опираться на строгую и осознанную систему логических заключений, свойственных особому авторскому методу научного мышления. Следование единой логике становится жестким условием математизации знаний для их представления в виде прямых вычислительных экспериментов по моделированию изучаемых явлений природы, ставших ныне поверяемыми с помощью компьютерных алгоритмов.
Поиск точной логики познания естественного мира и построение на ее базе нового аналитического инструментария возможно исключительно и только путем философского постижения авторской методологии творчества. Процесс получения знаний о природе и мире всегда происходит на почве исторических исследований, ведущих к сосредоточению логики и совершенствованию языка описания сложных явлений, переходящих затем в практические технологии или методы управляемого воздействия на естественные процессы.
По мере осмысления и практического формирования прикладной теории обязательно должны проступать горизонты более совершенного и осознанного мировоззрения, в первую очередь для самого автора.
Ключевым направлением аналитической работы является поиск путей практического использования имеющегося комплекса знаний, вечно вопиющего о своей неполноте для решения внешне элементарных инженерно-технических задач. Такое положение дел считается естественным и общепринятым в современной прикладной и вычислительной механике сплошных сред, чем и поддерживается постоянная творческая активность всех инженеров-гидромехаников.
Механика сплошных сред и ее математические методы издревле претендуют на особую значимость в определении моделей мироздания, наполненных подвижным энергонесущим эфиром. Гидромеханическая модель мира отличается обязательным обоснованием всех видов взаимодействий между элементарными смежными объектами, происходящими посредством непрерывной среды со строго определенными физическими свойствами. Не претендуя на какой-либо всеобщий характер, идея вездесущего и мирообразующего эфира всегда существовала в естественнонаучной философии, и развитие науки всегда привносит множество фактов и логических заключений для углубленного развития идей о непрерывности материи. Историческая, философская и начальная математическая проработка данного вопроса и является предметом первой части настоящего исследования.
Во второй части книги рассматриваются вопросы непротиворечивого проектирования вычислительных систем для решения прикладных задач гидромеханики, в которых формальные законы трехмерной логики лежат в обосновании оптимальности сложных компьютерных алгоритмов. Это приводит к систематизации ключевых решений для специализированного функционального языка программирования, логически сосредоточенного на законах гидромеханики и обладающего достаточной полнотой для построения прямых вычислительных экспериментов, в том числе в понятиях древней троичной логики – трилектики ‑ на пути созидательного поиска непротиворечивых проектно-технических и чисто инженерных решений.
Истинная красота научных результатов, вновь и вновь озаряемая глубоким смыслом божественного провидения, привела к обретению хорошо известного классического тензорного подхода, образовавшего как необходимую математическую основу, так и вполне достаточное инструментально-вычислительное средство, способное с абсолютной достоверностью определить искомые законы механики и алгоритмические методы их однозначного представления средствами цифровых дискретных ЭВМ.
Обновляемые материалы настоящих исследований планируются к представлению в интернет по адресу: http://www.ShipDesign.ru/Khram/Tensor.html
Главной целью настоящей работы является исследование тензорных конечно-разностных моделей механики сплошных сред, приводящих к реализации эффективных прямых вычислительных экспериментов, допускающих применение гибридных численных схем и адаптивных компьютерных алгоритмов для решения широкого круга инженерных задач гидромеханики реальных жидкостей.
Перспективной задачей тензорного подхода является поиск новых математических формализаций и численных алгоритмов для моделирования нестационарных течений жидкости, основанных на линейных аппроксимациях главных реологических параметров (вязкости, упругости и сжимаемости) в пределах малого, но конечного объема подвижной сплошной среды.
Тензорные конечно-разностные модели позволяют в строгой форме определять как базовые расчетные объекты, так и применяемые к ним вычислительные операции цифровой дискретной ЭВМ, которые в явной форме сопоставляются с реологическими свойствами жидкости и законами гидромеханики, позволяя на всех этапах компьютерного моделирования контролировать качество численных решений.
Очень важно, что новые числовые объекты и расчетные операции не противоречат постановке задачи о сквозном распараллеливании вычислений на цифровой ЭВМ, соблюдая при этом формальную независимость расчетных операций вплоть до уровня каждой из элементарных частиц жидкости. Это же условие является необходимым для обеспечения сквозного анализа физического состояния всех вычислительных объектов в размерном виде, обеспечивающего непрерывный и повсеместный контроль корректности численного моделирования.
Как и ожидалось, логическая и математическая систематизация вычислительных операций для элементарных числовых объектов гидромеханики привела к построению концепции и законченных проектных решений по синтаксису и семантике внутренних связей специализированного функционального языка программирования, ориентированного на автоматическое построение вычислительных экспериментов в механике сплошных сред, в том числе учитывающего особенности построения гибридных решений в критических областях течения жидкости (на свободных границах и в зонах вихревого поглощения энергии).
И все же, изложенные в работе теоретические результаты все еще очень далеки от сколь-нибудь законченных или канонических утверждений. Предложенные тензорные модели и методы построения алгоритмов для постановки вычислительных экспериментов, отражают не более чем текущий опыт автора, завершающийся вечно ускользающим горизонтом поиска красивых и ясных решений задач прикладной гидромеханики.
Возвращаясь к истории естествознания, нельзя не отметить, что во многих из дошедших до наших дней естественно-философских работах сглаживаются логические и теоретические противоречия, если метафизические высказывания античных авторов соотносить с непременным наличием сплошной среды, переносящей энергетику взаимодействия в различных фазовых состояниях естественной материи. Полагая Галилея, Декарта и Ньютона основоположниками современной механики важно отметить, что в их формулировках фундаментальных законов движения всегда присутствуют и в разной форме особо оговариваются условия сосуществования и взаимодействия непрерывной среды, в том числе всегда окружающей условно твердые тела с непроницаемыми границами.
В определении настоящей работы использован термин тензорная математика *1, несколько отличающий общепринятое понятие тензорного исчисления *2 в сторону прямого, полного и однозначного описания пространственно-временных законов гидромеханики.
В истоках математических наук уже не одно тысячелетие стоят «Начала» геометрии Евклида *3 , векторные построения которой создают незыблемый фундамент определения законов статики, кинематики и динамики для любых инженерно-технических изысканий.
Основы современной механики, так же как и вычислительной гидромеханики, заложены во времена Ньютона *4 в терминах исчисления конечных разностей метода флюксий, которые ныне обрели всеобщее употребление в упрощенной форме анализа бесконечно малых и дифференциального исчисления Лейбница *5 , сводящего законы гидромеханики к бестелесной точке в системах дифференциальных уравнений в частных производных Эйлера *6 .
С появлением эффективных вычислительных машин, прикладная, или вычислительная механика Ньютона *7 вновь обретает возможность эффективного развития на пути прямого численного описания законов природы, в новом свете пересматривая двойственность непрерывной среды в рамках построения корпускулярно – континуальных алгоритмических процессов численного моделирования.
Безусловно, что сама по себе математика, пусть даже и вычислительная, не становится самоценным объектом исследований, а лишь представляется как постоянно развивающийся инструмент для решения каких-либо теоретических и сложных технических задач. Современная прикладная математика уже немыслима без вычислительной техники, всецело находящейся под контролем автоматизированных информационных систем и искусственного компьютерного интеллекта. Вычислительная математика требует существенно более строгого подхода к определению всех числовых объектов и расчетных операций, в том числе в синтаксических формальностях и семантических связях математического языка. Так, к примеру, в тензорно-векторных записях становится существенным положение сомножителей, чем уравновешивается форма записи множимого-множителя и делимого-делителя; более глубокие смысловые ограничения включаются в описаниях законов механики и в алгоритмах для их практического применения.
И все же, в условиях внешне стремительного развития технических достижений, сама вычислительная математика обновляется медленно и весьма эклектично. Стремление к фиксации исходных положений математического языка для механики точки не только поддерживает самобытный консерватизм точного мышления, но и отражается множественностью разноречивых научных школ.
При этом все школы остаются в самостоятельном свободном поиске численного решения всевозможных прикладных задач, жестко сдерживаемом критериями по корректности и надежности дискретной аппроксимации классических уравнений математической физики, открыто указывающих на ограничения «докомпьютерного» языка математики для реализации новых вычислительных моделей, что более всего проявляется в задачах механики сплошных сред.
Упования на исторически выверенные математические модели и излишнее стремление к строжайшей преемственности в достижении сложных инженерных результатов, ныне заметно ограничивают творческие потенции и явно диссонируют с научно-эстетическими предпочтениями нового программистского сословия.
Вычислительные мощности современных компьютеров создают условия для быстрого и повсеместного внедрения сложнейших логических, математических и аналитических моделей для решения широкого круга задач гидромеханики, включая проектирование, производство и эксплуатацию морской и авиационной техники. В то же время традиционные и наиболее сложные для практической реализации "докомпьютерные" математические модели механики сплошных сред, как и ожидалось, словно в эпоху возрождения оживляют старые инженерные науки и фундаментальные идеи отцов современной гидромеханики: Зоммерфельда, Жуковского, Максвелла, Кельвина, Эйлера, Бернулли, Ньютона, Декарта, вплоть до Аристотеля, Эмпедокла, Анаксагора и Фалеса, заложивших в свое время базис не только инженерно-аналитических, но и прямых численных методов прикладной гидромеханики и физики в целом.
Богатство проявлений компьютерного мира математики и аналитической механики, как вполне материализованных аналитических и логических инструментов, стало возможным ввиду особых свойств новых языков математического мышления - языков программирования, не допускающих недомолвок и пустословия в изложении технической мысли, и дающих добротные экспериментальные материалы для поверки новых и оценки античных инженерных изысканий.
Многолетний авторский опыт реализации прямых вычислительных экспериментов в гидромеханике подтверждает широкие возможности нового и очень своеобразного машинного языка – алгоритмического языка вычислительной математики, богатого по своим функциональным возможностям и неограниченного в практическом поиске совершенных аналитических законов механики сплошных сред.
Нельзя ли в таком случае поставить задачу разработки специального математического языка, изначально ориентированного на прямое описание числовых объектов и расчетных процессов, однозначно отображающих законы механики сплошных сред на архитектуру современных цифровых вычислительных машин, аппроксимирующих изменчивые пространственные поля гидромеханики с помощью больших дискретных числовых массивов?
Настоящее исследование начиналось из курса лекций по теории корабельных волн Александра Николаевича Шебалова, прочитанных им на кафедре гидромеханики Ленинградского кораблестроительного института в середине 80-х годов. Огромные вычислительные интегралы-операторы Кочина для корабельного волнообразования, определенные в рамках теории функций комплексного переменного, в те годы удавалось сворачивать к вполне прозрачным тензорным формализациям с анизотропными свойствами относительно осей действия гравитационных сил и направления движения корабля или подводной лодки вблизи свободной поверхности.
Нестройные начала тензорной теории складывались из чисто механистических построений, учитывающих кинематику взаимодействия подвижного тела и свободной поверхности. Компьютерные процедуры по-простецки настраивались на желаемые физико-алгоритмические операции из аналитических функций, и, как оказалось, не без успехов. Однако в математической основе таких искусственных моделей оказывались совсем уж простенькие формулы из «школьного учебника».
При активной поддержке А.Н.Шебалова первым чисто тензорным достижением стало решение задачи, в которой параметры ядра сингулярного интегрального уравнения удалось втиснуть в обратный трехмерный псевдо-тензор-диполь. Инварианты эвристического тензора собрались из нелинейной численной оптимизации параметров волн Герстнера на условно большом удалении от ядра, и – численное решение задачи о движении тела вблизи свободной поверхности получилось.
Классическая школа прикладной корабельной аэрогидромеханики в лекциях Ярослава Иосифовича Войткунского и Вальтера Борисовича Амфилохиева изобиловали инженерными решениями, в которых теоретический анализ пронизывался экспериментальными эмпириками и электрогидродинамическими аналогиями. Да, собственно, и корабельные учебники с изложением идей Кельвина, Жуковского и Прандтля целенаправленно вели к пользам морской гидромеханики, достигаемым всеми доступными теоретическими и экспериментальными средствами. В такой научно-инженерной среде тензорные формализации численных решений становились необходимым и довольно эффективным инструментом создания унифицированных алгоритмов для моделирования различных течений жидкости.
Тензорные записи вычислительных объектов и операций оказались на удивление эффектными и удобными для решения интегральных и дифференциальных уравнений гидромеханики, для попутных геометрических построений расчетных схем, и даже для анализа экспериментальных материалов об испытаниях моделей судов в замечательном гравитационном опытовом бассейне Ленинградского кораблестроительного института. Во всех случаях это приводило к углубленному пониманию сути и смысла математических моделей и вычислительных операций на ЭВМ, однако теоретическое выражение пользы тензорной математики сдерживалось немотой поиска универсальной записи для столь красивых, понятных и невыразимых на языке формул чувств.
И словно зная о безысходности поиска связей в математическом и алгоритмическом языках, по странным впечатлениям тех давних дней середины 80-х, Борис Валентинович Мукосеев специально и только для наших гидроаэромехаников прочитал курс лекций о «тензорных математических моделях», переработанных для углубленного понимания именно прикладных задач гидромеханики. Удивительный курс тензорной математики сводился к иллюстрации полноты и точности тензорного определения законов движения в механике реальных жидкостей. И, как следствие, получались недоопределенными другие модели аналогичных математических представлений в теории упругости, электромагнетизме, и в прочих идеализированных сплошных средах и неньютоновых жидкостях.
Этого было уже вполне достаточно для определения пути в сторону тяжелого подъема к точному тензорному описанию трехмерных законов гидромеханики, однозначно задающих динамические процессы с элементарными континуальными объектами, всегда сохраняющими свою внутреннюю геометрию и физические размерности (с выходом из матричных ограничений тензорного исчисления на прямое описание законов гидромеханики в понятиях обобщенной тензорной математики).
Несколько быстротечных встреч в начале 90-х с Юрием Михайловичем Давыдовым, автором метода «Крупных частиц жидкости», популяризатором и выразителем глубочайшей философии вычислительных экспериментов в аэрогидромеханике, создали самую благоприятную почву для методичного построения искомой трехмерной тензорной математики. В результате, излагаемые в этой книге математические закономерности и идеи о численных решениях задач гидромеханики практически полностью покрываются глубокими идеями метода «Крупных частиц жидкости», благосклонно подкрепленные подборкой книг и статей с авторскими напутствиями Ю.М. Давыдова.
Невозможно представить более благоприятных условий для проведения исследований законов чистой гидромеханики, нежели в стране всепроникающей морской деятельности, на острове Сахалин. Остается только выразить искреннюю благодарность жене и невольному соавтору, Анне Вениаминовне Файн, воистину познавшей цену безбрежных морских влечений, беспросветных математических мытарств и нескончаемых поисков вчерашнего дня.
В тексте книги широко используются разнообразные геометрические понятия и их кинематические аналогии, связанные с формализованным представлением трехмерных пространственных объектов и алгоритмических операций над ними, всегда ассоциируемых с малыми подвижными континуумами жидкой среды *8 и их своеобразными метафизическими аналогиями. Отмечая, тем не менее, что нигде в этой работе не вводится каких-либо новых математических понятий или необычных физических законов, все же необходимо изначально определиться с особой терминологией и специальными математическими обозначениями, построению и обоснованию которых посвящено излагаемое в книге исследование.
Прямые вычислительные эксперименты гидромеханики с использованием цифровых дискретных ЭВМ, могут использовать только разностное представление пространственных физических полей, задаваемых ограниченным количеством аппроксимирующих узлов в пространстве. Динамика изменения этих полей также определяется дискретными этапами вычислений во времени.
В настоящей работе повсеместно используется жесткое условие о линейности всех интерполирующих функций, применяемых как для аппроксимации пространственных полей, так и к течению физических процессов внутри вычислительных этапов. Это сильно ограничивает контекст использования всех вычислительных объектов и расчетных операций, жестко связывая их с требованиями алгоритмизации, и необходимостью постоянного контроля и коррекции физических свойств сплошной среды, выполняемых непосредственно в процессе проведения вычислительных экспериментов.
В этом случае многие понятия и определения современной математики и традиционного тензорного анализа становятся избыточно обобщенными, что приводит к недостаточности исходных условий и неоднозначности физической интерпретации моделируемых процессов; к отсутствию необходимой строгости в построении вычислительных объектов; к неопределенности всех вычислительных операций и к необычайной сложности компьютерных алгоритмов в целом.
Тензорные формализации вычислительных объектов и операций существенно упрощают логику построения новых математических моделей гидромеханики, сводя их непосредственно к структурам данных и алгоритмам современных ЭВМ. К сожалению, используемая здесь трехмерная тензорная математика, хоть и является совсем малой частью современного тензорного анализа, все же для сведения ее записей к канонической форме, приходится пользоваться новыми обозначениями и особыми объяснениями тензорных объектов и операций. Поэтому, в тексте книги, где это возможно, в сносках будут доопределяться используемые термины и математические операции. Здесь же, во вводном разделе, вкратце приводится глоссарий и объяснения используемых математических операций и вычислительных объектов.
В определении координатных систем и векторных величин воспользуемся обобщенными терминами теоретической гидромеханики и понятиями математической теории поля:
Скаляры– эти величины вполне определяются своими численными значениями при заданных единицах измерения, например, как: время, длина и масса. Скалярными параметрами определяются также реологические (инвариантные) свойства сплошной среды, как: плотность, вязкость, упругость, сжимаемость (метрики, объемы и ориентация базисов) и др.
Векторы– это особые вычислительные объекты *9, в точности характеризующие местоположение точек в абсолютной или локальной системах координатных отсчетов; задающие пространственную ориентацию и масштабные параметры моделируемых объектов – элементарных континуумов жидкой среды; а также направление действия сил и реакций в рамках законов аналитической механики для крупных частиц жидкости и поляризованных корпускул.
Тензоры – пространственные композиции (симплексы *10 из базисных векторов или координатных осей, однозначно определяющие геометрические преобразования между различными системами координат и задающие линейные законы для описания физических свойств сплошной среды внутри и в ближайшей окрестности малых векторных триад – крупных частиц жидкости.
По физической сути тензор II ранга наиболее близко соответствует понятию аффинор а, введенного в использование Людвигом Прандтлем в книге «Гидро- и аэромеханика» [1932], где тензором называлась только симметричная часть аффинора, а выделяемая антисимметричная часть аффинора определялась в качестве особого вектора вращения.
Тензорные операции с элементарными объектами гидромеханики, их свойства и правила арифметических преобразований наилучшим образом соответствуют определениям, принятым в работе Дж. Астарита и Дж. Маруччи «Основы механики неньютоновских жидкостей» [1978], от нотации и смыслового содержания которых в этой книге не делается значительных отклонений.
В целом же, используемая здесь тензорная математика ограничивается использованием тензоров не выше второго ранга, всегда представляющих пространственно-кинематические процессы в малых объемах трехмерного пространства. Однако, несмотря на изначальные ограничения на разнообразие вычислительных объектов и операций с ними, изложение выходит за рамки тензорного исчисления повсеместным использованием двух дополнительных смешанных тензоров, которые не формализуются в рамках матричной алгебры. В основах математических записей особо оговаривается местоположение сомножителей одночленных выражений, в которых умножаемая (трансформируемая) тензорно-векторная величина всегда располагается слева от множителя (по аналогии с делимым – слева, и делителем справа). В качестве такого множителя чаще всего будет использоваться геометрический тензор формы крупной частицы жидкости, или обобщенные тензоры ее внутренней энергии, инерции, плотности и т.п.
Векторное исчисление составляет математическую основу современной геометрии, гидромеханики и электромагнетизма, всех явлений и процессов в океане и атмосфере, в законах теоретической гидромеханики и механики сплошных сред. Векторное описание пространственных объектов и методы геометрического представления непрерывных процессов берут свое начало из работ механиков XVII века Рене Декарта и Исаака Ньютона, создавших векторное исчисление в абсолютных координатных системах классической механики.
Вводя локальные системы координат для элементарных подвижных и деформируемых частиц жидкости, изначально ограничим рассмотрение принципов дальнего механического взаимовлияния, чтобы законы механики для близкого взаимодействия смежных частиц могли определять как большие внешние силовые воздействия, так и интенсивные инерционные реакции и значительные внутренние деформации элементарных гидродинамических объектов. Это позволяет сохранять декартовы базисы с евклидовым пространством для каждой из локальных систем отсчета, а все законы кинематики жидкости и механики ее трансформаций представить в виде линейных пространственно-временных зависимостей в простейшей тензорно-векторной форме.
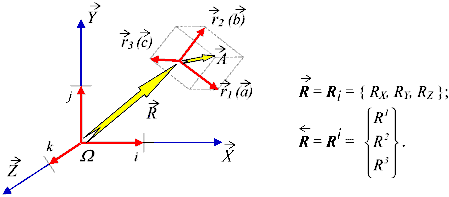
Рис. 1. Локальный базис ri местной системы координат образуется тройкой базисных векторов – ортов единичной длины.
Для удобства представления аналитических выражений, векторные величины будем обозначать различными способами:
1. 
– формальное обозначение векторной величины, где прописная буква R означает, что вектор измерен в проекциях с центром в единой абсолютной системы координат, а стрелка, направленная вправо обозначает, что векторные компоненты также измерены в проекциях абсолютной системы отсчета. Если стрелка направлена влево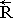 
, то величины векторных компонент считаются спроектированными на базисные оси какой-либо отдельной крупной частицы жидкости, обладающей собственным или дуальным базисом, связанным с глобальной системой координат с помощью геометрического тензора формы этой элементарной частицы.
2. Ri – определение векторной величины с помощью буквы и нижнего индекса, обозначающего наличие координатных проекций вектора на базисные оси двух- или трехмерного пространства. Такие компоненты вектора называют ковариантными. Если индекс у любого типа векторов или тензоров показан сверху, как: Rj, то это означает, что величины координатных проекций отмерены в связанной локальной системе отсчета элементарной крупной частицы жидкости, а компоненты такого относительного вектора называют контравариантными.
3. Векторная величина, при необходимости анализа каждой из ее компонент, записывается в виде матрицы-строки для привязки к абсолютной системе отсчета, или матрицы-столбца – для ее связывания с локальным базисом. В окончательном виде векторные величины могут быть заданы одним из указанных способов:
- вектор в проекциях абсолютного базиса;
- тот же "длинный" вектор в локальном базисе.
Как это стало общепринятым в компьютерных моделях, в локальном базисе вместо наглядных буквенных обозначений координатных осей, нередко используются цифровые индексы с порядковыми номерами тех же векторных компонент.
Местная или связанная система координат в трехмерном пространстве математически формализуется в виде локального базиса, образуемого некомпланарными векторами произвольной (ненулевой) длины, которые определяют собственный масштаб единичных ортов внутри локальной системы координат. В проекциях глобальной системы отсчета компоненты локальных тензоров могут быть представлены в виде строки из трех базисных векторов или ‑ трех столбцов координатной матрицы из 9 чисел:
Новый математический объект, определяемый с помощью трех условно единичных базисных векторов или матрицы компонент этих векторов, называют геометрическим или базисным тензором 2-го ранга, или просто – тензором.
Простейшими примерами локальных систем отсчета в технике являются местные координаты, в том числе связанные с подвижными объектами, как самолет, корабль или автомобиль.
По формальным признакам иногда скалярные величины называют тензором нулевого ранга, а векторные величины – тензором первого ранга.
По аналогии, в местной системе отсчета единственным образом могут быть представлены проекции единичных ортов исходной абсолютной системы координат, что образует обратную матрицу, или – дуальный базис: 
, как:
,
В определении местных координатных систем используется правило, что собственные оси внутри локального базиса всегда представляются строго ортогональными (взаимно перпендикулярными) и ортонормированными (с собственной единичной мерой). Это означает, что из локального базиса абсолютная система координат смотрится как некая другая – «как бы локальная» (дуально связанная или - обратная), косоугольная и неортонормированная система векторных отсчетов.
Точно также операция умножения вектора на произвольный (невырожденный) тензор II-го ранга, всегда переводит его из собственного декартового базиса в некую произвольную, в том числе видимую изнутри как ненормированную и косоугольную внешнюю координатную систему, основанную на связных (дуальных) базисных осях.
Введенные таким образом геометрические правила позволяют при определении законов гидромеханики опираться на важное свойство локальных систем координат, всегда обладающих собственным декартовым базисом в локальном евклидовом пространстве, и дающих возможность определять базовые законы гидромеханики в явной или даже в канонической форме.
Вычислительная техника и систематическое программирование вернули к жизни многие антично-философские обобщения, усилив их древнюю словесную логику строгими правилами современных алгоритмических языков, обогатив давние учения новыми функциональными возможностями искусственного интеллекта современных вычислительных систем.
Поиск специальных математических начал гидромеханики, подобно созданию сложных технических объектов, происходит на пути прямого логического проектирования, с последующим всесторонним обоснованием принятых технических решений.
На начальных этапах такого проектирования можно линейно выстраивать ключевые умозаключения, выбираемые только из необходимых физических предпосылок диалектическими методами, как своеобразно позиционированный выбор между гиперболизованными логическими противопоставлениями. Последующая функциональная оптимизация внутренних свойств для новых логических объектов, строго связанных с условно внешними операциями над ними, потребует удовлетворения жестких критериев единственности и достаточности принятых в качестве базовых законов механики и специальных математических инструментов, в свою очередь сводящихся к независимому трехстороннему обоснованию всего комплекса проектных решений в рамках непротиворечивой логики – трилектики.
Непротиворечивые методы логического проектирования могут быть жестко связаны с технологиями создания сложных программных комплексов, реализующих все этапы численного моделирования в гидромеханике, от подготовки числовых объектов, до графической визуализации результатов и интерактивного управления проведением вычислительного эксперимента в целом. В диалектическом противопоставлении здесь встают технологии чисто функционального и декларативного программирования, которые применяются к особо организованным структурам данных и исполняемым последовательностям машинных кодов.
Непротиворечивость проектирования программ достигается трехсторонним рассмотрением всех вычислительных объектов и физических процессов с позиций достижения наиболее эффективной реализации конкретной прикладной задачи вычислительной гидромеханики.
|
Исходя из диалектического учения Платона, это метод восхождения к новым знаниям на пути синтеза и разрешения всевозможных логических противоречий, как пути познания ведущего к вершине понимания технической задачи в виде сложного, но единого инженерного комплекса. В терминах оптимального проектирования это путь «снизу-вверх», от анализа и накопления необходимых предпосылок и конкретных технических решений, к определению универсальных логических объектов и законов их динамического взаимодействия. Этот этап завершается достижением условной вершины знаний об изучаемых предметах и явлениях, называемой Платоном «божественной». С такой высоты уже нечетко видится фундамент искомого предмета исследований, зато очень точно поименовывается условно новое направление чисто технического познания природы.
На поверочном пути «сверху-вниз», как минимум, должны быть жестко связаны все аналитические результаты: обоснована оптимальность новых теоретических построений; доказана достаточность найденных проектных решений и единственность их технической реализации. Для инженерной задачи только на обратном поверочном пути проектирования могут быть определены окончательные параметры всех составляющих единую систему устройств и ее комплектующих звеньев; указаны области совместного существования различных технических решений и определены функциональные ограничения новых технико-теоретических разработок.
По формальным признакам такой всесторонний анализ результатов проектных исследований уже выходит за рамки одномерного диалектического познания, так как в обоснование технических решений закладываются качественно другие независимые критерии и инородные количественные оценки, обусловливающие оптимальность позиционирования относительно диалектически противопоставляемых концепций. И все же, именно двухстороннее диалектическое изучение проектных крайностей, гиперболизация частных технических «достоинств», ярко освещает недостижимость слишком простых технических результатов, в том числе обусловленную динамической нестабильностью, как для отдельных конструкций, так и для всего будущего инженерного сооружения или сложного вычислительного эксперимента в целом.
Это означает, что диалектический метод может представляться лишь одномерно-скалярным аналогом в выборе направления поиска в трехмерном логическом пространстве, в котором формальные противоречия можно развести по ортогонально ориентированным базисам, добиваясь поиска независимых оценок и оптимальных количественных критериев, изначально присущих противопоставляемым теоретическим концепциям.
При создании компьютерных алгоритмов, в рамках диалектики останутся не только скалярные проектные критерии, принимаемые в противопоставляемых системах логических определений, но также и тензорные математические объекты, которые логически фиксируются в абсолютной и в локальной системах отсчета, устанавливаемые как связные, дуальные, а по сути – взаимно обратные объекты математической теории поля.
|
Применение троичной логики в физике лучше всего иллюстрируется аналогиями из трехмерного пространства – времени, в котором описываются, анализируются и решаются все прикладные задачи механики сплошных сред.
Важно отметить, что математические законы гидромеханики позволяют разрешить многие физические парадоксы, и в том числе обосновывать ограниченность энергетических взаимодействий и устойчивое существование подвижной среды именно в трехмерном абсолютном пространстве с идеальным временем.
К сожалению, для прикладных задач вычислительной гидромеханики до настоящего времени еще нет строгих определений даже для элементарных законов механики близкого взаимодействия смежных частиц жидкости, не установлены строгие математические зависимости между динамическими инвариантами движения и деформациями ограниченных жидких континуумов. Фактически отсутствуют универсальные теоретические разработки для численной реализации законов движения и кинематики деформируемых сред, математически строго не определяются пространственно распределенные реакции внутри и в окрестности жидких континуумов при их взаимодействии с внешними и внутренними силовыми полями; так же как и при локальных энергетических воздействиях на границы крупных частиц жидкости.
Современный тензорный анализ, используемый для описания законов движения жидкости, обладает значительным аналитическим заделом. Как оказалось, при минимальных понятийных уточнениях тензорная математика приводит к существенно более строгим и однозначным выражениям при числовой фиксации состояния элементарных частиц жидкости, включающим специальные правила для реализации динамики взаимодействия смежных числовых объектов в рамках аналитической механики и математической теории поля одновременно. Обобщенные тензорные числовые объекты определяют свойства жидкости и механику взаимодействия смежных частиц в строго линейной постановке аппроксимационной задачи.
Ограничивая теоретические исследования поиском эффективных численных решений прикладных задач гидромеханики, можно разделить исходную постановку проблемы на три взаимосвязанных и одновременно независимых объекта чисто прикладных исследований в области проектирования и компьютерной реализации прямых вычислительных экспериментов в гидромеханике, как таковых:
1. Троичная логика исследования элементарных числовых объектов, вычислительных процессов и комплексных математических моделей, нацелена на создание условий для непротиворечивого проектирования и оптимального построения сложных прикладных вычислительных экспериментов в механике сплошных сред;
2. Поиск путей построения специальных функциональных языков программирования, управляющих адаптивными алгоритмами вычислительной гидромеханики, и предназначенных для автоматизированной постановки задачи и контролируемого решения прикладных задач гидромеханики, в том числе со сложными режимами течения жидкости;
3. Тензорный математический аппарат вычислительной гидромеханики, формализующий описание фундаментальных законов существования и динамики энергоемкой непрерывной среды.
– координаты узла сеточной области Ω на момент времени T [м]; – координаты смежной точки в следующий момент времени [м]; 
– полная скорость частицы жидкости в абсолютной системе отсчета [м/с]; – вектор скорости относительно подвижного центра частицы жидкости [м/с];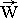 
– вектор приращения скорости (ускорения) для частицы жидкости [м/с2]; 
= 
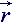k = rik – геометрический тензор формы крупной частицы жидкости [м3]; 
= DD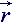i – тензор локальных скоростей (приращений скоростей) [м3/с]; 
= ·
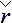= / – тензор конвективных скоростей [1/c];
= Δi – тензор течений внутри крупной частицы жидкости [м3/с];
= 
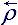j = ρ ij – тензор плотности, или внутреннего состояния жидкой частицы [кг/м3];
= · = м ij – тензорная масса жидкой частицы, как смешанный тензор, приводящий внутренне состояние жидкой частицы к абсолютной системе отсчета [кг];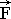 
– результирующий вектор массовых (объемных) сил [Н; кг·м/с2]; 
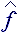– тензор напряжений на границах жидкой частицы [Н·м2; кг/с2]; 
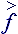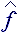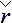= · – напряжение внутри и в ближайшей окрестности жидкой частицы [Н/м; кг/2]; 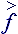н = 
· / Λ – условный тензор вязких напряжений , : [кг/м/с; Н·с/м2];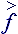г =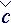 
· / Λ – условный тензор упругих напряжений , 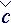: [кг/м/с; Н·с/м2] Сноски
[1] Математика – наука о количественных отношениях и пространственных формах действительного мира.
[2] Тензорное исчисление - математическая теория, обобщающая векторное исчисление и матричную алгебру. Математический язык матричной алгебры недостаточен для построения законов механики элементарных частиц жидкости, так как в трехмерном пространстве необходимо еще и точное определение двух смешанных тензоров, задающих деформационные и конвективные характеристики в кинематике движения жидкости.
[3] Геометрическое (векторное) 
пространство Евклида характеризуется существованием метрики, которая позволяет однозначно измерять расстояние между любыми двумя точками. В трехмерном пространстве в декартовой системе координат такое правило задается квадратичной зависимостью: r2=|2R-1R|2=(2x-1x)2+(2y-1y)2+(2z-1z)2.
Здесь и далее левые нижние индексы задают собственные отметки точек или объемных вычислительных объектов в геометрическом пространстве Евклида.
[4] Исаак Ньютон (Newton Isaac, 1643-1727).
[5] Готфрид Вильгельм Лейбниц (Leibniz Gottfried Wilhelm, 1646-1716).
[6] Леонард Эйлер (Euler Leonard, 1707-1783).
[7] Механика Ньютона подразумевает существование абсолютной системы отсчета, задающей однозначные и линейные преобразования координат с любым из локальных базисов, жестко связанных с подвижными телами или вмороженных в элементарные континуумы сплошной среды. При этом для любых систем отсчета всегда справедливы кинематические идеализации абсолютного времени, последовательно текущего во всех законах механики и всегда единого для любых пространств и материальных объектов.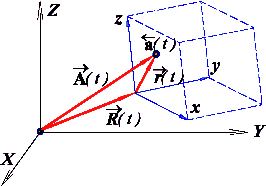
[8] Малый континуум включает в себя сплошную среду в ближайшей окрестности локального базиса, заданного базисными осями трехмерного конечноразностного тензора, внутри которого все физические характеристики и законы механики жидкости аппроксимируются линейными зависимостями.
[9] Векторные величины представляются с помощью композиций из числовых величин их проекций на координатные оси, либо с помощью задания длины (модуля) и угловой ориентации (направления) векторов. Последние определяются в виде специальных полярных, цилиндрических или сферических систем координат, имеющих криволинейные изолинии, и потому в данной работе они рассматриваться не будут.
[10] Симплекс – минимальное количество базисных векторов, задающих линейное пространство в ближайшей окрестности пространственной точки. В трехмерном пространстве симплекс составляется из 3 векторов, в двумерном – 2, в одномерном – 1 вектора.
... Оглавление 1. Технико-исторический обзор трехмерных физических обоснований непрерывной и вездесущей среды. 2. Логика создания вычислительных моделей и компьютерных алгоритмов. 3. Тензорное представление алгоритмов вычислительной гидромеханики. 4. Опыт построения программных алгоритмов.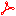 ... Заключение