 =
=
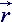 i= rij, based on neighbouring nodes of estimated frame, forming elementary nonplanar simplex.
basis vectors. It is rather convenient to call new nonplanar object by geometric or basis tensor of the second trace, or simply - tensor.
i= rij, based on neighbouring nodes of estimated frame, forming elementary nonplanar simplex.
basis vectors. It is rather convenient to call new nonplanar object by geometric or basis tensor of the second trace, or simply - tensor.BULLETIN OF THE FAR EASTERN BRANCH, RUSSIAN ACADEMY OF SCIENCES.
The Bulletin FEB RAS. 2004. ¹ 1
 V.N.Khramushin, A.V. Fine
*
V.N.Khramushin, A.V. Fine
*
The Tensor Mathematics Notation for the Computational Fluidmechanics Algorithms.
Vasily N. Khramushin, Anna V. Fain (Special Research Bureau for Automation of Marine Researches , FEB RAS, Yuzhno-Sakhalinsk).
The results of generalizations of the numerical solutions executed when searching for the effective computer algorithms for the applied fluidmechanics problems have been presented. Finite sizes differentials, which Isaac Newton had yet worked with, have been formalized within the context of tensor calculus enabling linear interpolation of physical parameters between adjacent spatial cells and their knots. It turned out that the computing instrument like this not only simplifies the traditional numerical scheme notation, but also is able to pretend to peculiar theoretical analysis of some phenomena and paradoxes in the continuous field mechanics. In this fluidmechanics model, the convective flow components are considered. There is a possibility to verify the physical correctness of simulated processes immediately during the calculations. Some new phenomena and paradoxes of the fluid mechanics, which the principle possibility and quality of computational experiments depends on, are elaborated.
The base of mathematical rules of spatial objects building and methods of their space-temporary interactions analysis may be connected with works of the mechanical engineers of XVII century Rhenium De Cart and Isaac Newton, determined laws of vector interactions in absolute counting systems of classical mechanics.
De Cart, proceeding with mathematization and geometrization of physics, determined the measure of local motion of one object relative to another: "If one of two men moves with the help of ship, and another stands ashore motionless... that there is no any advantage neither in the motion of the first, nor in the rest of the second". This meant entering of the common vector laws for description of physical objects and processes in absolute and in local counting systems, nominally concerning with different active objects.
Newton submits the main rules of vector geometry to mechanics: "Absolute space, in the main, regardless to external, remains always identical and stationary. Relative - is the measure or some limited active part...". It turns out, that absolute space is always relative, but physical objects can be mathematically strictly connected with local counting systems derived from them. Newton determines also the main world scalar value - time: "All motions can be quickened or slowed, but current of absolute time can not be changed."
"Time and space forms the receptacle of themselves and the whole existing. At time all is situated in the sense of the sequences, but in space - in the sense of position order ". These determinations are quite enough to build new computer variants of mathematical description of elementary objects, operations and computational fluidmechanics algorithms.
However the world of computer models not quite simply displays in modern mathematics, presenting the laws of fluid motion in form of systems of differential equations in quotient derivatives. Is it possible to use finally-differential objects and operations, inherent digital COMP, as independent mathematical instrument? De facto mathematical bases of such approach are well designed by Y.Ì.Davidov [3] as method of large particles, sometimes called by method of final volume.
Computational experiments in fluidmechanics in completed type need complex presentation of information about greater fields of fluid currents, to which as laws of fluid mechanics, as different algorithms for adapting the numeral solutions to real conditions must be strictly used. In such statement, the computational experiments designing must be guided by theoretical bases of "functional programming", in which the initial data control both applicability of mathematical functions, and structure of computational algorithms as a whole.
The traditional finally-differential approximations of fluid motion equations, after their algorithmic formalization, with appointed share of conventionality can be considered in the capacity of another fluid mechanical model, qualitative distinguishing from initial record of the mechanics laws in the manner of systems of differential equations in quotient derivatives. The optimization of computational models for increasing the rates of computations, checking the physical criteria of solutions correctness and using the adaptive methods for expansion of area of engineering computations applicability is quite often executed in notions of algorithmic operations for special numeral objects inside the COMP. Especially actual and the most difficult such analysis of computational models in accordance with the agreement of physical characteristics of fluid in special conditions, appearing as inside the calculated area, so on free borders. The practical experience of computational experiments realization, connected with the decision of engineering problems of fluidmechanics, required the practical formalization of that actions, which are necessary as for acceleration of calculated algorithms (including the optimization of cycles of calculations), as for the unification of procedures, simulating the laws of fluidmechanics on internal breakups and external borders of calculated area (provision of functional invisibility of borders). The natural mathematical instrument is the classical tensor calculus for building of elementary computational objects [5], more exactly - its small part, simulating the linear intercalation operations with elementary physical objects in dimensioned type (not above tensors of II rank - for 3-measured space). With this the curtailment of numeral schemes to tensor form brings to the original canonical writing of initial equations, which are realized on digital COMP. more quickly and efficiently. As the practical experience showed designing and realization of computational experiments, new models in tensor presentation perform deep physical sense and can be applying for solving of appointed circle problems of mechanics of entire media, including an analytical form.
Nevertheless the most important element of considering work is searching for universal mathematical instrument for building of computational experiments in fluidmechanics, which would have deep and full analytical possibilities and simultaneously allowed to use automatically different physical laws depending on criteria of processes development in entire media, would allow through paralleling of all calculations up to each elementary particles of fluid.
Introductory determinations. Computational experiments in mechanics of entire media base upon their own mathematical device of final differences, in base of which the approximations of unceasing functions by limited amount of supporting values lay, distributed among discrete cells of digital COMP memory [3]. The differential calculus, basing on analysis of infinitesimal values and equitable for analog designing devices, is not applicable in full measure for digital models of discrete approximated physical fields and torn calculated time intervals of kinematical processes.
It is reasonable to simplify the problem, limited only by linear interpolating functions in node points of space, with linear extrapolation of physical values on calculated time intervals. The classical tensor calculus in full measure defines the necessary rules of linear interpolation within the elementary particles of fluid, closed between adjacent nodes of calculated space. With this tensor formalizations greatly increase the possibilities of computational fluidmechanics, as point or scalar values of separate differential equations are changed by their volumetric tensor analogues, containing full determination both externals powers, and kinematics of internal deformation for all elementary particles of fluid.
The possibility of numeral solution of fluidmechanics applied problems practically is always complicated by approximation restrictions or unfulfilled criteria, which correct account is possible with using of special adaptive decisions and hybrid numeral schemes, based on heuristic, empirical or experimental confidant dependencies. For conservation of principle possibility of hybrid algorithms use, as well as for the purpose of through controlling of executed calculations quality during the designing of computational experiments, it is very important to support physical non-discrepancy of all computational objects and numeral operations with them [6]. Then: 1) elementary objects of fluid mechanics must be determined in dimensioned form only, in strict accordance with given set of fluid characteristics; 2) all computational operations must be comply with the concrete laws of fluid mechanics, and using of the intermediate analytical transformations to simplify the initial mathematical models is not admissible; 3) calculated algorithms must watch automatically the attribute of numeral components to the united absolute and bound local coordinate systems, providing necessary changes between them, with unconditional controlling of accordance with all physical dimensionalities.
The observance of so hard complex of logical rules limits noticeably the use of new algorithms to reproduce directly a lot of traditional problems of computational fluid mechanics, and especially - based on differential equations of high order. However these algorithms do not contain the principle restrictions for numeral direct modeling of mechanics' problems of any entire media. And sometimes some of realized computational experiments are compared better with natural observations, as analytical decisions and traditional numeral methods until do not allow to get the analogous qualitative results.
The main prerequisites for computational experiment project building. The traditional physical interpretation, as well as numeral decision of fluid mechanics problems, is based on two geometric ideas about current of fluid, interconnected and greatly differing in form: these well known differential formalizations of currents by Euler - on fixed net and changing of meanings hydrodynamic fields in its cells , and by La Grange - with fixation of laws of conservation into each moving particles of fluid, forming special active and irregular net too.
The most effective computational experiments in fluidmechanics are based on methods of division of decisions on physical processes, in which the stage of modeling with use of La Grange free fluid particles is changing into process of concordance of physical fields on Euler's motionless nodes of calculated net. Formally these two stages of first-order integration, which reconstruct together the decision of traditional differential equation of second order mechanics.
La Grange's free particles within the own geometric sizes must behave themselves like power-consuming objects, which partly waste the energy of their own motion and accumulate it inside itself in interaction with surroundings ( picture 1).
 Formally Newton's vector law can be built with the help of tensor multiplying operation, where external power F
can be determined in absolute coordinate system, and reaction W - in local base, freezed in elementary deformed particle of fluid. Tensor mass of
fluid particle M will be able not only to perform role of energy accumulator of onward motion, but also take into account inertial characteristics
of deformational and rotary movements of fluid within this elementary fluid particle.
Formally Newton's vector law can be built with the help of tensor multiplying operation, where external power F
can be determined in absolute coordinate system, and reaction W - in local base, freezed in elementary deformed particle of fluid. Tensor mass of
fluid particle M will be able not only to perform role of energy accumulator of onward motion, but also take into account inertial characteristics
of deformational and rotary movements of fluid within this elementary fluid particle.
Picture 1. Elementary object of computational fluidmechanics - large particle of fluid, being always encircled unceasing medium with similar characteristics, reacts on total external influence taking into account prehistory of its non-free motions and internal deformations.
Determination of base objects in space and time. The spatial description of large particles of fluid is executed in extended tensor notation in two interconnected coordinate systems. The first - absolute, or motionless (Euler), net of node values, which is the united and global system of computational experiment. The computational objects, connected with the absolute counting system, are marked the capital letters. The second - local, which emerges the natural base of concrete large particles of fluid, participating in free (La Grange) motion on own path, and in which the internal characteristics of this particle of fluid are determined. Counting outs of time are always absolute and scalar.
The capital letters mark the values, measured in absolute counting systems (Rk - the vector of coordinates for point in space, Ò - counting out of time from the beginning of computational experiment). The small letters mark measured inside local (active) bases (rk - vector of point local coordinates, determined in bound counting system inside concrete particle of fluid). Then in spatial indications by capital letters the counting outs of big size are marked, commensurable with scale of calculated area, the small letters mark the final differences, which are used as linear differentials.
By left upper indexes we will be mark the current counting outs in time, to which the computational objects or processes are concerned. The index + --is the following counting out of time. If time in computational experiment is connected with calculated times k, that: +F = k+1F that comply with counting out of time: +T=k+1T=0T+(k+1)·t, where t is a calculated time interval. Left lower indexes are the numbers or indexes of net area spatial cells , which can be interpreted as Euler's quiet coordinate system or absolute one. Source location of liquid particulates are marked by the left lower indexes and capital letters { J,K }, spatial marks of fluent liquid particulates are marked by small indexes { j,k }and some adjacent accounting cell will be marked by the lower index +.
All right indexes are the tensor identifiers and they also identify belonging to the accounting system. Lower indexes bend the object to the absolute coordinate system and upper indexes to the local basis properly. The vectorial heads can change indexes, in this case head vectored to the right ® marks belonging to the absolute accounting system (lower index), and the head vectored to the left ¬ to the local accounting system (upper index). Tensor amounts are marked by double indexes or nooks Ù - absolute; Ú- local; >,< and ´ - mixed accounting systems.
Local coordinate system shapes mathematically in the form of local basis, formed by noncomplanar heads with an ordinary length:  =
=
 i= rij, based on neighbouring nodes of estimated frame, forming elementary nonplanar simplex.
basis vectors. It is rather convenient to call new nonplanar object by geometric or basis tensor of the second trace, or simply - tensor.
i= rij, based on neighbouring nodes of estimated frame, forming elementary nonplanar simplex.
basis vectors. It is rather convenient to call new nonplanar object by geometric or basis tensor of the second trace, or simply - tensor.
On the analogy, projections of ordinary versors of absolute coordinate system can be presented uniquely in the local accounting system, that forms dual
basis :  =
= 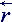 j = r ij
j = r ij  -1, where
tensor's components can be formed by simple geometric constructions of absolute basis free ordinary intervals in the cuttings-off in the parts of parallelograms
within the local basis (figure 1).
-1, where
tensor's components can be formed by simple geometric constructions of absolute basis free ordinary intervals in the cuttings-off in the parts of parallelograms
within the local basis (figure 1).
Figure 1. Local basis  of local coordinate system is formed by trey basis vectors - versors
of conventionally ordinary length
of local coordinate system is formed by trey basis vectors - versors
of conventionally ordinary length
 =
= 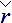 ·
·
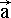 – converts vector from the absolute coordinate system to the local one. In the time of transition of local vector from the one coordinate
system to another, it does not change its differential - difference context. To surgery the definite (restricted) vector from the local accounting system to the
absolute (figure 2) it is necessary to add supporting point coordinates of local basis:
– converts vector from the absolute coordinate system to the local one. In the time of transition of local vector from the one coordinate
system to another, it does not change its differential - difference context. To surgery the definite (restricted) vector from the local accounting system to the
absolute (figure 2) it is necessary to add supporting point coordinates of local basis: 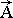 =
= 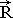 +
+
 ·
·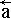 .
.
Mixed tensors are formed in a similar way, and they become apparent in the manipulation of determination of motion laws of continuum. Unfortunately, it is impossible to employ the usual means of matrix algebra in the construction of tensor amounts for hydrodynamical objects, its descriptive capability is not hold out for determination of mixed tensors. All laws of tensor algebra [4] are correct to the full.
Summation convention. If the same index comes across twice in one-term formula- one time, as upper and another, as lower, then the summation of conformable formulas in the run of this index of amounts 1,2,3 is supposed. Such index is called dummy.
Checking up on concurrence. Any index which is not dummy owe come across in all components of formula or as upper either as lower index. Any formula, containing indexes different from dummy, must be explanated as the system of equations, when each index takes up amounts 1,2,3.
Ought to notice, that upper indexes, coming across in the consequent of monomial expression, amount to this expression lower indexes.
In indicial form manipulation of general tensor multiplication: 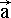 =
=  ·
· 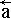 can
be presented as: ai =rij · aj, where indexes, standing under the multipliers right on different levels, are called dummy,
and their emergencies in the manipulations of product subtend summation of vectorial components through this index:
can
be presented as: ai =rij · aj, where indexes, standing under the multipliers right on different levels, are called dummy,
and their emergencies in the manipulations of product subtend summation of vectorial components through this index:
ai = åj (rij · aj). (9’)
Multiplication manipulations can be made with an increment or dip of trace of composite product. Thus, as a result of multiplication of vector by tensor: (rij · ak) tensor of the third trace is formed- with three indexes. Such manipulations do not have singular manual context therefore are not considered. Besides, it is inhibited to use them in usual manipulations even as algebraic generation intermediate result. Multiplication with dipping of tensor trace, such as scalar product of vectors: q=ai · bi ( projection of one vector on another), usually is used in analysis of computation objects features and it is also inhibited to use it in the multiplication manipulations because dipping of trace result is meant the loss of assumed vectorial objects information. Prohibitions on trace changing in making of product manipulations allow to avoid logical faults in regrettable disposition of tensor and vectorial multipliers in monomial expression.
Hard terms on satisfiability of structure and multiplication manipulations for analysis vectorial and tensor object in this work are necessary for building special computation algorithm, which on formal condition of computation objects belonging to actual accounting systems allow to automate all coordinate generations as in immediate solution of mechanics matters so in presenting their results on computer.
It is convenient to use left indexes for computation objects binding (large fluid parts): in space - left lower index, in time - left upper index. Lack of the left indexes subtends that determination occurs to the current situation and to the all elemental cells of accounting field properly.
ΩT 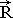 – main point coordinates, where R points count away from zero of absolute
coordinate system, head vectored to the right ® points the belonging to it, W determine location of main in
estimated field; T – the point of time away from the beginning of computation experiment.
– main point coordinates, where R points count away from zero of absolute
coordinate system, head vectored to the right ® points the belonging to it, W determine location of main in
estimated field; T – the point of time away from the beginning of computation experiment.
+t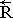 – refer on neighbouring point, in Ωt
– refer on neighbouring point, in Ωt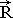 point, removing to (+) with regard for basis point of fluid elementary volume Ω (large part) in a time t. Head vectored to the left
¬ shows, that "long" vector of absolute counts is taken to the local basis projection , but herewith it was connected with current
location of large fluid part.
point, removing to (+) with regard for basis point of fluid elementary volume Ω (large part) in a time t. Head vectored to the left
¬ shows, that "long" vector of absolute counts is taken to the local basis projection , but herewith it was connected with current
location of large fluid part.
Also dynamic conception excess of speed in the shape of resulting differences (figure 3): 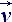 = D
= D = +
= + - 0
- 0  . Reologic features of fluid become apparent in computation
experiment in the shape of tensor specifiers of elementary rated objects internal features, for which persistence of fluid flow reologic characteristics must
be presented in the course of computations, in parallel with realizing of control of criterions of existing the most computed solution.
. Reologic features of fluid become apparent in computation
experiment in the shape of tensor specifiers of elementary rated objects internal features, for which persistence of fluid flow reologic characteristics must
be presented in the course of computations, in parallel with realizing of control of criterions of existing the most computed solution.
Basic operations of computational fluidmechanics construction. General fluidmechanics principles in tensor form allow to define not only kinematics of
elementary fluid parts, but also their internal deformation in a strict correspondence with intensions from the external force actions. Let following dimensional
field in absolute (global) coordinate system be determined as given data for building of computation experiment in fluidmechanics:{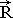 }[ì]
– coordinate field of double points; {
}[ì]
– coordinate field of double points; { } [ì/ñ] – rate field; {
} [ì/ñ] – rate field; { }[êã] – tensor field of internal features for each
fluid part.
}[êã] – tensor field of internal features for each
fluid part.
In net domain local computation objects are comprehended- as elementary large fluid parts, in which manual parameters of fluid flow are determined in the same
coordinate system:  [ì3] – tensor of large part form;
[ì3] – tensor of large part form;  [ì3/c] – local (convectional) rates;
[ì3/c] – local (convectional) rates;
 [Í·ì2] – intension tensor.
[Í·ì2] – intension tensor.
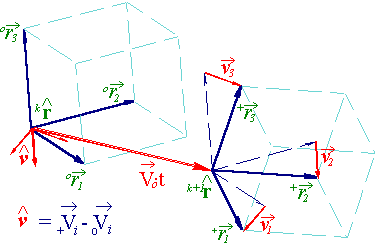 Figure 3.Tensor of local rates is formed by deformation blases of large fluid part basic vectors in rated
time interval.
Figure 3.Tensor of local rates is formed by deformation blases of large fluid part basic vectors in rated
time interval.
Laws of motion for deformed fluid part in tensor form not complicated than usual arithmetical manipulations, which are similar in shape, in point of fact as for the external force, so for internal deformations. This allows to handle rather simple analytic dependences, which use the effects of accumulation and following emission of mechanical energy, obtained in the result of external interactions between neighbouring rated cells.
Internal energy of elementary deformed parts (if rotational or dipole effects be in tensor of convectional rates) can define changing in pointing of reaction on external force, and also changing of fluid part persistence amount, this enlarges the use of general laws of motion (for organic and inseparable universes).
1. Newton vector law for deformed part:  =
= 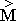 ·
· 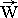 =
= ·
·
 ·
·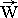 . (1)
. (1)
2. Viscidity intension tensor for Newton's fluid **: 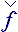 Í
=
Í
= 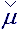 ·
· H =
H = 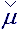 ·
· 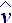 H·
H·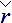 .
(2)
.
(2)
3. Tensor of elastic intension for Gook's solid body: 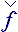 Ã =
à = 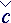 ·(
·( +
+
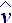 r·t)·
r·t)· 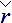 =
=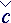 ·(
·( 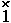 +
+
 r·t), (3)
r·t), (3)
where local rates tensor is determined by an algorithm as: 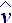 = +
= + i - 0
i - 0 i
(figure 3); and dominant reologic constants are represented formally as tensors, for which the following formulas are correct:
i
(figure 3); and dominant reologic constants are represented formally as tensors, for which the following formulas are correct: 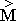 = M
i j =
= M
i j =  ·
·  = rij·r
jk -tensor of persistence in projection on absolute accounting system, and determinations:
= rij·r
jk -tensor of persistence in projection on absolute accounting system, and determinations:  -
tensor of density and internal energy accumulation;
-
tensor of density and internal energy accumulation; 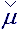 ,
, 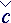 - tensors of dynamic viscidity and hardness
of fluid.
- tensors of dynamic viscidity and hardness
of fluid.
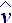 ·
·
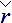 =
= 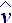 ·
·  -1=
-1=  , in the result of it tensor of
rates in the mixed coordinate system obtained, which can be denoted as tensor of convective rates in total of physical properties. Obtained tensor is without dimension
in space argument, therefore its amounts can be put in correspondence with reologic parameters of fluid.
, in the result of it tensor of
rates in the mixed coordinate system obtained, which can be denoted as tensor of convective rates in total of physical properties. Obtained tensor is without dimension
in space argument, therefore its amounts can be put in correspondence with reologic parameters of fluid.Use the splitting of convective rates tensor on
deviatoric  * and globular tensors:
* and globular tensors:  =
=  0 +
0 +
 *. Tensor of globular compressibility
*. Tensor of globular compressibility  0 is presented in the shape of scalar matrix, all
elements of which are equal among themselves, in convective rates tensor it characterizes scalar divergence (compressibility) of fluid flows and is connected with
the first reologic parameter of fluid:
0 is presented in the shape of scalar matrix, all
elements of which are equal among themselves, in convective rates tensor it characterizes scalar divergence (compressibility) of fluid flows and is connected with
the first reologic parameter of fluid: 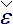 – dynamic compressibility coefficient.
– dynamic compressibility coefficient.
Deviatoric tensor  * has null linear invariant: tr(
* has null linear invariant: tr( *)=0, that formally indicate the
peculiarities of the rest fluid flow irretractability. Tensor of viscid potential difference is obtained by discrimination alternating part from the matrix of deviatoric
tensor
*)=0, that formally indicate the
peculiarities of the rest fluid flow irretractability. Tensor of viscid potential difference is obtained by discrimination alternating part from the matrix of deviatoric
tensor  *, that is formally in accord with rotation of fluid elementary parts and inertial potential difference, connected with it:
*, that is formally in accord with rotation of fluid elementary parts and inertial potential difference, connected with it:
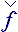 =
= 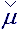 ·
·  H =
H =
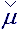 · (
· (  *-
*-  * T)/2. The other symmetrical tensor
will be define proper deformation of fluid elementary part, which can be related to elastic potential difference:
* T)/2. The other symmetrical tensor
will be define proper deformation of fluid elementary part, which can be related to elastic potential difference: 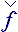 Ã
=
Ã
= 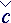 ·
·  Ã · t =
à · t = 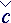 ·(
·(  *-
*-
 * T)·t/2. Properly, general tensor of internal intensions:
* T)·t/2. Properly, general tensor of internal intensions: 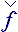 = (
= (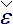 ·
·
 0+
0+ 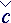 ·
·  Ã)·t +
Ã)·t +
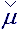 ·
·  H.
H.
Usually tensor determination of reologic parameters are adapted in anisotropic peculiarities of continuum, but in case of analyzed computation models fluid traditional scalar physical parameters must be presented as orthogonal tensors, determined with the help of conformable scalar matrixes.
The prehistory of elementary rated objects deformation is connected with density tensor  , on Lagrange's level of computation
experiment allow to sum up the fluid large parts taking part in free (corpuscular) motion. With exception of density tensor on all rated stages elastic and
viscid fluid peculiarities in the shape of constrained tensors
, on Lagrange's level of computation
experiment allow to sum up the fluid large parts taking part in free (corpuscular) motion. With exception of density tensor on all rated stages elastic and
viscid fluid peculiarities in the shape of constrained tensors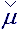 è
è 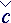 will be appear, which real
physical quantities depends on present tensor's form condition
will be appear, which real
physical quantities depends on present tensor's form condition  . If the model of optimum fluid on quiet mesh points Ω
. If the model of optimum fluid on quiet mesh points Ω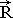 is used in computation experiment, than main being of computations will be reduced to the support of medium isotropy, when tensors
is used in computation experiment, than main being of computations will be reduced to the support of medium isotropy, when tensors
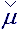 è
è 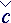 are formed by diagonal components equal in value.
are formed by diagonal components equal in value.
Properties of computation operations and elementary objects. All operations of computation fluidmechanics are made in a different way to the utmost, that is necessary for controlling of physical correctness of modeling processes for each taken individually fluid part and, as the need arose, using of hybrider schemes in subdomains, where the mode of current changing and automatic changing of motion laws using and their mathematical models. Three types of operations are concerned with computation objects:
1) logical operations, or empirical. Such physical laws as: if convective rates tensor exists  , than it induces tensor of densities
, than it induces tensor of densities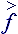 by law (2), and etc. Such operations define the method of formation and methods of analysis of tensor's objects condition, as well as taking of decisions about
mathematical models changing along the computations;
by law (2), and etc. Such operations define the method of formation and methods of analysis of tensor's objects condition, as well as taking of decisions about
mathematical models changing along the computations;
2) composition operations, applying to the amounts with an equal physical dimensions on condition that they are determined and constructed in the same basis. Composition can be applied to the complex objects in conditions where operations of automatic correlation of counting systems and physical dimensions are determined;
3) "product" operation applying to the objects, linked components of which are situated in dual counting systems only. Inhibit the increment of tensor's trace in the product operations. Special algorithms, based on physical arrangement problem of computation experiment realization, must be determined for vectorial and tensor objects construction.
Computation objects are provided by the following properties:1) scalar and invariant amounts, for example time t, can de involved into product operations only, with any objects; 2) vectorial amounts take part in composition operations with comparable amounts and in product operations with tensors, if it is necessary to change the coordinate system. It is invalid to apply multiplication of vectors for dyads constructing; 3) tensor amounts determine the physical particulars of fluid elementary parts, their geometric deformations [1], cinematic particulars and the other dynamic processes of solid medium. Tensors also can be involved as in the composition operations with the comparable tensors, as in the product ones with linked vectorial and scalar objects. Using to tensor objects fundamental fluidmechanics laws are enunciated, and automatic design and analysis of these objects form logic-mathematical problem of realizing of computation experiment in fluid mechanics.
Moving of check point in space, jumping at one pass of the first (Euler's) step of computation experiment, can be presented as enumeration of point coordinates
in a local counting system to the absolute, with regard to time lag t :
+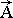 =
= 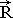 +
+  ·t +
·t + 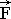 ·
·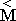 ·t2/2
+ (
·t2/2
+ ( +
+ 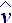 ·t +
·t + 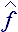 ·
·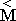 ·t2/2)·
·t2/2)·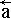 ... ( 4 )
... ( 4 )
The following step of computations can be determination of vector of local rate increment for this point (acceleration), then judging by its field new field
of external forces and internal energy for initial large parts are recreated:
+ =
=  + (
+ (  +
+ 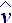 ·t )·
·t )·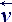 .
( 5 )
.
( 5 )
Thus the first step of computation experiment, in which the control of solution correctness on field { r }is followed; correlation of persistence
conditions of physical parameters into elementary fluid meshes{ M }; and to this end - recalculation of new "external forces" for each large fluid part:
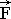 =
= 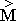 ·
·  ·
·  =
=  ·
·
 ·
·  ·
·  .
.
We will call the scheme of solution splitting for equation of the second sequence on the physical processes as division of computations process into two steps, on every of which differentiation of first order is realized. If the spatial differentiation of rate field is realized on the one step, then according to it the new field of tensions is is computed, prompting carrying out, on the second step, the computation of fluid parts blases according to the rate field corrected by accelerations and using convective redistributions flows to agree the conditions of the persistence, and the field of force is restored again, but now for new instant of time.
Under the spatial differentiation the result of operation is carried from the nodes of counting field to the formed large fluid particles' centers, but these centers are displaced toward the rate of free moving of particles. It means that the second step of calculations is complicated by additional algorithms of interpolation into accounting field and extrapolation in rent nodes on external borders of this field.
If disposal mass forces take participant in problem, such as free fall acceleration, that they will constantly displace the path of free particles moving, which must recover at the cost of liquid bounce on the second step. It is necessary to search for the changeover mechanisms of the external force field by tense condition to free surface, to example, for outage of such mechanism of fluid particles transformation.
Computation experiment construction.
Process of fields transformations, in case of the source requirement of node point coordinates persistence { }, can be divided
into three stages:
}, can be divided
into three stages:
I. Kinematics. The new field of node points:
{+ =
= 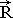 +
+  ·t +
·t + 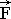 ·
·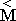 ·t2/2
}( 6 )
·t2/2
}( 6 )
The field of convective forces is formed by algorithmic buildings of tensor:
{ 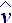 } = { +
} = { + i - 0
i - 0 i
} ( 7 )
i
} ( 7 )
Accounting condition of the new internal characteristics field:
{ +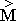 } = {
} = { ·+
·+ } = { (
} = { ( +
+ 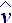 ·t)·
·t)· };
};
{+ } = {
} = {  ·(
·(
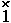 +
+ ·t) } ... ( 8 )
·t) } ... ( 8 )
II Dynamics. The collation of fluid rheology is realized here with the current condition of the computation model. Let the law of persistence of motion amount
is determined on spaced time interval on stages of :
+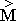 ·
· =
= 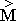 ·(
·(  +
D
+
D ), on the basis of (8):
), on the basis of (8):
D = ( +
= ( +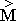 -
- 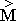 ) ·
) ·
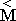 ·
· =
=  ·
· ·t, ( 9 )
·t, ( 9 )
the Newton's equation is resulted in the form of Euler, correct for large particle on quiet nodes of the accounting field:
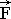 =
= 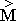 ·
· ·
· =
=  ·
· ·
· ·
· .
( 1* )
.
( 1* )
The obtained expression contains in itself tense condition of fluid, which can be explained by reologic characteristic to computation model of the current:
{ 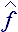 } = { +
} = { +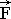 i - 0
i - 0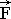 i
} or
i
} or 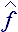 =
=  ·
· ·
· ·
·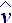 =
= 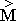 ·
· ·
·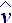 .
.
In shape new equation corresponds to writing of tensions in Navie-Stoksa's equations. Real fluid rheology is formed in the manner of laws (2),(3),
concerned with tensor of convective rates  . Then the matter of calculations can be converted to correlation of characteristic of
computation and physical fluid models.
. Then the matter of calculations can be converted to correlation of characteristic of
computation and physical fluid models.
As a result of different derivation in expression (9) thridementional acceleration component was lost, which can be received while analysis of moving of
the particle with variable mass, without considering deformation:
M = det( 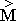 ), r = det(
), r = det(  ),
),
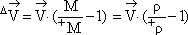 (10)
(10)
Considered computation model always provides fluid with characteristics of condense, viscosity and elasticity [1]. There were not considered the tensor deformations
of large particle form  in obtained equations, that allows to consider the fluid inwardly it isotropic. By separation of the
diagonal tensor
in obtained equations, that allows to consider the fluid inwardly it isotropic. By separation of the
diagonal tensor  0, such, that trace from the remainder will be equal
0, such, that trace from the remainder will be equal  * will be a zero:
* will be a zero:
 =
=  0 +
0 +  * (tr
* (tr * =0),
we will get the tensor of globe compress:
* =0),
we will get the tensor of globe compress:

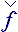 0 =
0 = 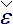 ·
· 0·t,
( 11 )
0·t,
( 11 )
where tensor components 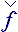 0 define the pressure,
0 define the pressure, 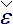 –coefficient
of the dynamic compression.
–coefficient
of the dynamic compression.
By separation of an alternating particle of matrix  *, which defines the rotation of large particle as regard to adjacent ones,
will be received tensor of viscous tensions:
*, which defines the rotation of large particle as regard to adjacent ones,
will be received tensor of viscous tensions:
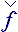 Í =
Í = 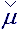 ·
· H =
H =
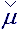 ·(
·(  * -
* -  * T)/2. ( 12 )
* T)/2. ( 12 )
Remained symmetric tensor is linked with elastic deformation (6):
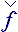 Ã =
à = 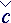 ·
· Ãt =
Ãt =
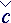 ·(
·(  *-
*-  * T)·t/2. ( 13 )
* T)·t/2. ( 13 )
Full tensor of internal tensions: 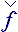 = (
= (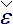 ·
· 0+
0+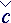 ·
· Ã)·t
+
Ã)·t
+ 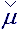 ·
· H. ( 14 )
H. ( 14 )
Considered dynamic coefficients 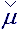 ,
, 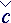 and
and 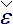 , are differed from kinematic,
on scalar density coefficient r. Under the tensor of tension action
, are differed from kinematic,
on scalar density coefficient r. Under the tensor of tension action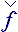 , the
particle gets the incremenation of internal (isolated) motion rate:
, the
particle gets the incremenation of internal (isolated) motion rate:
D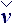 =
= 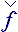 · t /r
( 15 )
· t /r
( 15 )
If the current is formed, than, for accounting time lag, tensor of rates incremenation D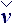 must compensate tensor of convective rates by itself in accounting time interval:
must compensate tensor of convective rates by itself in accounting time interval: 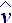 ·
·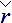 +
+
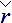 · D
· D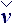 = 0. This formula is sharp at this stage of calculations, as
far as large particles blas is not taken into account in a time t.
= 0. This formula is sharp at this stage of calculations, as
far as large particles blas is not taken into account in a time t.
The last formula is sharp, if the large particles blas is not taken in account in a time t.
3. Static. It is necessary to conduct the recovering of the rate field on the terminating stage under the incremenations calculated on the second one, herewith deformational motions round the static particles gravitational centers are considered.
It is necessary to go from tensor D 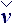 , determined in local base, to the mixed tensor, where the
local characteristics rest on absolute accounting system:
, determined in local base, to the mixed tensor, where the
local characteristics rest on absolute accounting system:
D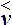 = D
= D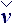 ·
· .
( 16 )
.
( 16 )
This tensor is not concerned with the local geometry of basis  .
.
To turn to the base net we will build the new local basis, rested on quiet node, and in the capacity of adjacent ones uses spatial points displaced in time :
+ = ++
= ++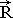 i - 00
i - 00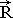 i,
( 17 )
i,
( 17 )
Revealing formula (7), used during the building of the local rates tensor: 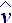 = +
= + i
- 0
i
- 0 i, in rates, connected with the new basic vectors
i, in rates, connected with the new basic vectors 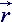 , we will get an algorithm of calculation
of the new rate field:
, we will get an algorithm of calculation
of the new rate field:
+ =
=  + Si
+ Si ·D
·D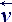 i,(18
)
i,(18
)
which sums up the incremenations of rate from surrounding large particles.
Formulas (15) - (18) reveal the main algorithmic buildings, allowing to use of Newton's converse law: 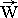 =
=
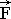 ·
· 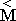 .
.
Accelerations obtained in vectorial form: for the particle with variable "mass" (10); and for portioned mass forces, must be interpolated with the centers of cells on the initial nodes of the accounting field.
Wordy the stages of calculations are defined as follows:
I - on quite Euler's net the calculations of the portioned current characteristics are realized;
II - the internal characteristic of the fluid particles are considered with the aim of tensor "masses" building , in which pre-history of deformation is saved. Also here the iterative processes of determination are organized, in which the correlation of computation rheology and physical models of fluid current is taken place;
III - the characteristics of a current are interpolated with displaced in La Grange motion gravitational centers of large particles on the initial nodes of computative area. On this stage we can consider the conditions on free (fluid) borders, where instead of interpolation algorithms in broken nodes of non-regularized net inwardly the computative area will be used the extrapolation with the aid of abroad centers of special (border) fluid particles .
Computation ambience. The characteristics of tension tensor 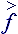 in the process of calculations can be unadjusted
with rheology of considered fluid. To get an iterative algorithm of physical and computative parameters correlation current tensor
in the process of calculations can be unadjusted
with rheology of considered fluid. To get an iterative algorithm of physical and computative parameters correlation current tensor
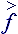 can be divided into true tensor and deviator. This will allow to include the possible tensions in the current dynamics,
and to reflect deviatoric ones from borders of the adjacent particles interfacing, therefore damping the further development of negative deviation. Compatible with
it tensor of convective rates is corrected, from which deviation components are subtracted. In point of fact, it is an usual mechanism of free and reflecting borders,
only used relaxational correlation of computational solutions.
can be divided into true tensor and deviator. This will allow to include the possible tensions in the current dynamics,
and to reflect deviatoric ones from borders of the adjacent particles interfacing, therefore damping the further development of negative deviation. Compatible with
it tensor of convective rates is corrected, from which deviation components are subtracted. In point of fact, it is an usual mechanism of free and reflecting borders,
only used relaxational correlation of computational solutions.
If initial conditions, when started the process of decision, do not correspond to the laws of fluid current, then value of the deviation tensor can be as big that there will be destruction of approximated criterions. In this case it is possible to use the amendments to the reologic parameters of fluid, which must agree (or bring nearer) physical and computative current characteristics by iteration method. The latest is very important for the idealized fluids, the numerical algorithms for which will be always reduced either to tacit schemes, or to iteration processes.
Correctness control for executable decision is reduced to checking of interpolating formulas acceptability. As an example of the decision destruction we can quote on the event, when one bound of the particle, as a result of free motion in given rates field, will overtake the opposite bound of the same particle. This can be avoided by the reduction of calculation time interval. Formula, showing such maximum permissible interval, are usually called the criterion of decision stability in time. The well-known Courant's criterion exactly corresponds to above determination.
With checking on the spatial approximation the deal is more complicated, as far as conformable criteria are linked not only with initial conditions, but also with local geometric computative area features. On debugging stage of computation experiments realization method of visual checking on forms of computative areas, drawn on computer graphic screen can be offered.
In accordance with formula (8): +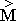 = (
= (  +
+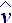 ·t )·
·t )· , mass of the particle is really a summer of local rates tensors. On the first stage
, mass of the particle is really a summer of local rates tensors. On the first stage 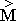 is used for determination of internal characteristics
of particles, on the third one - by means of = -1 is described an interaction of the adjacent fluid particles is described due to
is used for determination of internal characteristics
of particles, on the third one - by means of = -1 is described an interaction of the adjacent fluid particles is described due to 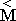 =
=
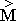 -1. Computation model always contains three main characteristics of fluid: compressibility; viscosity; bounce, in the process
of correlation of the stated voltages intensities, can bring to critical mode or change the mode of fluid current (we mean the formation of streams, rotational
layers and cavitational breaks).
-1. Computation model always contains three main characteristics of fluid: compressibility; viscosity; bounce, in the process
of correlation of the stated voltages intensities, can bring to critical mode or change the mode of fluid current (we mean the formation of streams, rotational
layers and cavitational breaks).
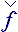 =
= 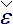 ·
· 0·t·+
0·t·+ 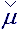 ·
· Í·+
Í·+
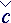 ·
· ã·t·=
ã·t·= 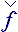 0 +
0 +
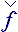 Í +
Í + 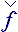 Ã. ( 14*)
Ã. ( 14*)
Tensor of voltages (14) can be defined as characteristical polynomial for the internal condition of the computation particle, in which fluid rheological parameters click into place of main tensor invariants:
 0 : I ¹ 0 - compressibility;
0 : I ¹ 0 - compressibility;  Í : II
¹ 0 - rotation;
Í : II
¹ 0 - rotation;  ã : III ¹ 0 - a clean deformation, the other invariants
of these tensors are equal zero.
ã : III ¹ 0 - a clean deformation, the other invariants
of these tensors are equal zero.
If internal condition of the particle is considered without notice of computation nodes blas, then the requirement of compensations of local rates at the cost
of incrementations of rate caused by tensor of voltages can be put:
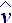 ·t +
·t + 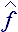 ·
·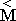 ·t2/2 = 0, ( 19
)
·t2/2 = 0, ( 19
)
from which, as summer of voltages may be tensor density remove:
+ =
=  + (
+ ( 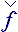 0 +
0 +
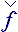 Í +
Í + 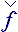 Ã.)·t2/2
@
Ã.)·t2/2
@  0 +
0 +  Í +
Í +  Ã.
( 20 )
Ã.
( 20 )
Consider two variants of tensor + destruction during the execution of one calculations tact, when
r = det(
destruction during the execution of one calculations tact, when
r = det(  ) reduces to zero.
) reduces to zero.
1. Cavitational break of density:
 Í - is not considered;
Í - is not considered;
 0 such that det(
0 such that det(  0 ) < 0 - ñîîòâåòñòâóåò ïîëþ ñ ðàçðåæåíèåì; corresponds to the field
with sparcification;
0 ) < 0 - ñîîòâåòñòâóåò ïîëþ ñ ðàçðåæåíèåì; corresponds to the field
with sparcification;
 * such that det(
* such that det(  0+
0+  ã ) = 0 - tensor of density reduced
to dyad, which can be determined by plane perpendicular to the main axis of the strain of bounce tensor
ã ) = 0 - tensor of density reduced
to dyad, which can be determined by plane perpendicular to the main axis of the strain of bounce tensor  ã.. If liquid
does not stand the negative pressure, then given plane must be used as free border, getting through the large particle.
ã.. If liquid
does not stand the negative pressure, then given plane must be used as free border, getting through the large particle.
2. Formation of free stream or turbulent rotation.
 Let accounting system will be connected with moving particle, subjected to translation deformation.
Let accounting system will be connected with moving particle, subjected to translation deformation.
On completive stage of calculations source rotational particle can turn the determinant of internal field of adjoint particle into a zero, where ro > 0. It is possible, in this case, to use the empirical algorithm of rotation transport from the first stage of calculations in tensor of "mass" of the third stage. Then the voltage will be taken down from an adjacent cell, and the particle in free motion will show peculiarities, typical of turbulent rotation. Presented algorithm is an empirical model, which can be used outside the approximated reduction of computation area, to receive proximate decision the net can be condensed near the rotation.
Simple examples of effective computational realization of method
Tensor arithmetic, used for designing of full and direct computation experiments in fluidmechanics, in general case always deals with real fluids, possessing full complex of rheological characteristic, which are imposed by linear/inverse restrictions within finite-difference scale of elementary accounting cells. The main illustrations were executed on the example of solution of hyperbolic problem about spreading the springy longitudinal waves (long waves in ocean), which allow the evident spatial solutions and therefore very opportune for physical interpreting of main computation processes.
1.Realization of computation experiments about long waves spreading in the ocean, built on basis of tensor model, under real modeling of long-wave processes in the ocean (tides, storm surges, earthquake waves) shows the good correspondence of the model to full scale observations. Tensor model possesses clear-cut dispersion characteristic (increase of the period during the wave motion over uneven bottom, or so called red shift); shows the good coordination with supervision for time of the long waves fading processes close to seaside (decrement of fading characterizes correctness of long-wave processes energy conservation of conditions); in the case of successful coordination of approximating criteria close correspondence of form and an order of following of long-wave pulse of modulated and real earthquake close to seaside shallow area (correct streaming of interference, dispersion and refractive processes for wave processes). There are always "convective" particularities of fluid current in tensor model, that is connected for traditional computational methods with need for modeling of currents with "nonlinear characteristics". Tensor model affords easily to use the hybrid schemes and introduce in solutions of different empirical restrictions, such as tidal geopotential, innate viscosity and surface voltages at passing of storm and deep cyclones. As far as the model is based on conceptions of solutions division on physical processes, that all foreign restrictions can be included or excluded in process of computational experiments undertaking.
2.An important confirmation of tensor equations correctness is the computational experiment of several flow-around objects of free form modeling by flow to ideal fluid (i.e. flow, the vorticity sources in which are absent). In this case not only the shown tensor restrictions are correct as regards to adjacent accounting cells, but also all distant accounting cells have active connections, realized on direct line strictly. This implies that modeling of objects flow-around by fluid can be reduced to simple integrating of moving body on its volume and ed surface. For this volume of solid is changed with equivalents dipoles, and surface - with vorticity sources. Such problem is worked upon successfully, including for several moving objects simultaneously.
3.Visualization of initial datas and demonstrative analysis of computational experiments results, wherein multivariate restrictions are presented on two dimensional field of computer graphic screen are occupies an important place in modern computation mathematics. Shown computational algorithms in this work are simple and efficient methods of recalculation of vector-tensor values between different coordinate systems.
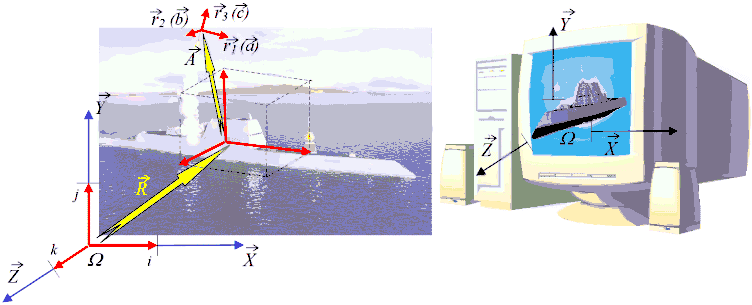
Figure 4. In management of shiftable objects multiple transformations of coordinate systems are always used, bound both with real objects
and with their representer in counting-solving devices and computer terminals
In many cases tensor transformations shown in work are actively used for quick and demonstrative building of two- three-dimensional interpolating procedures, working as transformation of coordinate systems, including nonorthogonal, possessing highest numerical efficiency.
The last example (figure 4), in case of free tensor basis use, can serve as original model of distant interaction between energy intensive corpuscles-quantas, that can be used for formalization of many laws of electromagnetic interactions successfully [2].
But the main result of the work is detection of relationship between the numerical description of large fluid particles and its rheological parameters and, as consequence, possibility of computational experiments setting up for unstable processes, allowing through processes of calculations control, including with adaptive using of physical laws in changing of current mode.
Bibliography
1. Àstarita G., Marucchi G. Elements of fluidmechanics of non -Newton's fluids, Ì.: Mir, 1978. 307 s.
2. Astakhov A.V., Shirokov Y.M. Physics course. Ò.2. Electromagnetic field. Ì.: Nauka, 1990, 384 s.
3. Belozerkovsky O.M., Davidov Y.M. Method of large particles in gas dynamics. Ì.: Nauka 1982. 370s.
4. Kilchevsky N.A. Elements of tensor calculation and its addition to the mechanics. Ì.: State publishing of technical-and-theoretic literature,1954. 167 s.
5. Mac-Connell À.G., Introduction into tensor analysis, Ì.: Nauka, 1963, 411s.
6. Khramushin V.N. Three-dimensional tensor mathematics of computational experiments in fluidmechanics // Effective calculations and its additions: Materials of All-Russian Science Symposium Ì.: ÍÈÂÖ ÌÃÓ, 2000. S. 114-117.
* Khramushin V.N. - Candidate of Science,
Fine A.V. (SRB-AMR FEB RAS, Yuzhno-Sakhalinsk)
** Hereinafter specially stipulate marks or indexes, denoting special physical peculiarities of mathematic objects will be used with dimensions with graphical tensor-vectorial notation.
Òåíçîðíîå ïðåäñòàâëåíèå àëãîðèòìîâ âû÷èñëèòåëüíîé ãèäðîìåõàíèêè, ñ.52-68
BULLETIN OF THE FAR EASTERN BRANCH, RUSSIAN ACADEMY OF SCIENCES, ¹ 1, 2004
V.N. Khramushin, A.V. Fine. The tensor notation of the computational fluidmechanics algorithms, ð.52-68