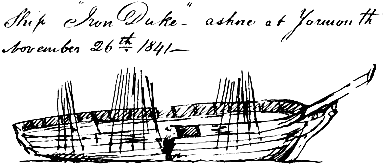Н.А. Мытник
КРАТКАЯ ИСТОРИЯ КОРАБЕЛЬНЫХ НАУК
(хронология событий с комментариями)
Глава 3. Период становления и революционного развития корабельной науки
( с 1746 по 1854 год)
(Продолжение)
События 1746 г.
- Морской академией России при участии сподвижника В.Беринга Алексея Чирикова
(1703-1748 гг.) составлен итоговый атлас русских открытий на Тихом океане, содержащий
около 100 карт.
Через три года в 1749 г. членом Петербургской и Берлинской академий наук
математиком Леонардом Эйлером (1707-1783 гг.), приглашенным для работы в
Россию в 1727 г. (в 1724 г. Петром I была основана Петербургская АН), издана книга
“Корабельная наука или трактат о строении кораблей и управляемости ими” (рис.25),
в которой он изложил основные законы теории корабля и оригинально применил математические
методы к изучению мореходных качеств судна, в частности, по параболической аппроксимации
строевой по ватерлиниям и определению метацентрического радиуса.
Краткая биографическая справка:
Леонард Эйлер, швейцарский математик, физик, астроном,
механик. Окончил Базельский университет, член Петербургской, Парижской
и Берлинской академии наук, Лондонского королевского общества, автор
свыше 800 работ (!) в области математического анализа, дифференциальной
геометрии, теории чисел, приближенных вычислений, небесной механики,
математической физики, оптики, баллистики, кораблестроения и гидромеханики,
сопротивления материалов, теории музыки и др. Разработал теорию движения
Луны и морских приливов, предложил метод определения долготы
по лунным расстояниям.
|

|
Книга Эйлера стала вторым после труда Бугера учебником для кораблестроителей
и была в разное время издана во многих странах. Особенно полезной она оказалась
ввиду того, что Эйлер изложил там основы аналитических приемов определения искомых
характеристик проектируемого судна.

Рис.25. Титульный лист знаменитого учебника по теории корабля Л.Эйлера "Корабельная
наука или трактат о строении кораблей и управляемости ими".
Уравнение остойчивости
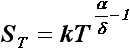 ;
;
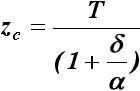 ;
;
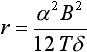 ;
;
h = zc + r - zg ;
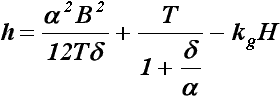 ,
(1749 г.)
,
(1749 г.)
где ST - площадь ватерлинии, м2; zc
- аппликата центра величины, м; r - поперечный метацентрический радиус,
м; h – начальная метацентрическая высота как основная характеристика остойчивости
судна, м; Т - осадка судна, м; d - коэффициент
общей полноты корпуса судна; a - коэффициент полноты
ватерлинии; В - ширина судна, м; zg - аппликата центра
тяжести судна, м; kg - коэффициент аппликаты центра тяжести;
Н - высота борта судна, м
(рис.26).
В своей работе Эйлер предлагает методы измерения остойчивости, развивает учение
о сопротивлении воды движению судна, о действии ветра на паруса и управляемости
корабля, решает задачу качки судна на тихой воде и выводит формулу для расчета периода
собственных колебаний судна.
Дифференциальное уравнение незатухающей качки:
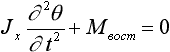
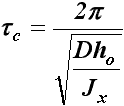
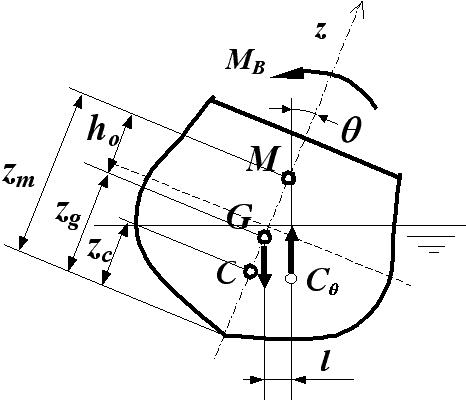
Рис. 26. Схема сил, действующих на накрененный корабль.
где Jx - момент инерции масс судна относительно продольной
центральной оси, кг·м2; ¶ 2q
/¶ t 2 - угловое ускорение поперечных
колебаний судна, рад/с2; Мвост= Dhoq
- восстанавливающий момент, н·м; D - весовое водоизмещение
судна, н; ho - начальная метацентрическая высота, м;
t с = 2p/wс
- период собственных поперечных колебаний или бортовой качки судна на
тихой воде, с; wс
- частота поперечных колебаний, 1/c; q
=q o сosw
ct - текущая амплитуда качки, рад.
Таким образом, с появлением в середине XVIII века учебников по теории корабля
Бугера и Эйлера искусство строить суда, передававшееся от отца к сыну, от мастера
к ученику, стало развиваться в науку, не имеющую тайн.
События 1749 г
- Русский корабельный мастер Гавриил Окунев на Адмиралтейской верфи спускает
на воду 66-пушечный линейный корабль “Александр Невский”, построенный по французской
технологической схеме, изученной им у француза М.Пангало, работавшего при Петре
I на верфи, и во время учебы во Франции с 1725 по 1731 г.
- Во время шторма затонул голландский корабль Ост-Индийской компании “Амстердам”
с грузом серебра и бургундского вина.
В 1752 г. в Париже издается первое сочинение Даламбера в области сопротивления
воды “Очерки новой теории сопротивления жидкости”, которое внесло существенный
вклад в развитие теоретической гидромеханики.
Интересным и важным с точки зрения проектирования судов событием в этом же году
явился выход в свет книги известного французского кораблестроителя, инспектора французского
флота, Дюамеля дю Монсо “Начала корабельной архитектуры”, в которой впервые
высказываются соображения о значении для проектирования судна прототипов
и математических методов в определении главных размерений. Монсо предлагает определять
длину боевых кораблей из условия размещения пушечных портов, а ширину и высоту борта
- по прототиповым значениям (L /B)o и (L
/H)o . Таким образом, размерения корабля предлагалось
находить исключительно из условий обеспечения вместимости и никакой связи
между характеристиками задания и водоизмещением пока не устанавливалось.
В работе обобщается установленная еще Дином практика определения водоизмещения судна
и соответствующей ему осадки после изготовления теоретического чертежа и конструктивных
чертежей корпуса судна.
События 1752 г.
- На Соломбальской верфи русский корабельный мастер Потап Качалов (1709-1767гг.)
строит первый бомбардирский прам русского флота “Дикий бык”.
- Гибель в Южно-Китайском море корабля голландской Ост-Индийской компании
“Гельдермалсен” с грузом китайского фарфора.
В 1753 г. Парижская АН объявляет конкурс на разработку ряда тем по теории
корабля. Результатом конкурса явились известные работы Эйлера, братьев Бернулли,
Бугера и других ученых, установившие методы вычисления элементов плавучести и
остойчивости по теоретическому чертежу, расчет нагрузки корабля, основы
учения о качке и напряжениях, испытываемых связями плавающего в воде судна.
Необходимо отметить также конкурсные работы, посвященные новым способам движения
судов. Интересно, что, если Д. Бернулли, Эйлер и другие французские ученые наиболее
перспективными считали бортовые гребные колеса, причем приводимые в движение мускульной
силой при помощи специальной механической передачи, английские ученые и кораблестроители,
как представители более развитой в промышленном отношении страны, предлагали наряду
с гребными колесами и гребные винты, в том числе приводимые во вращение паровой
машиной.
В целом этот год фактически закрепил научные достижения того времени в области
теории корабля и прочности и лишний раз подтвердил передовые позиции французской
кораблестроительной школы в Европе.
События 1753 г.
- Суд над русским вице-адмиралом Петром Бредалем, который в 1742 г. вернул
эскадру из 10 кораблей назад в Архангельск по причине ветхости кораблей и полученных
ими повреждений во время штормов на переходе из Белого моря на Балтику.
В 1757 г. выходит новая книга Бугера “О маневрировании судов”,
в которой ученый дает дальнейшее развитие своих исследований в области теории корабля
по маневренным качествам судов.
События 1757 г.
- Английский капитан Кампелл усовершенствует навигационный прибор типа секстана
- октан Гадлея, что позволяет ему измерять углы светил до 120о.
В 1759 г. в Берлине выходит книга Эйлера “Исследование усилий, которым
подвергаются все части судна при бортовой и килевой качке, и наилучший способ создания
при их сборке прочности, необходимой для сопротивления этим усилиям, без вреда для
положительных качеств судна”, которая может считаться первым сочинением исключительно
по прочности судна. В этом труде, в частности, рассмотрена критическая нагрузка
сжатого стержня, при которой он теряет устойчивость и которая с тех пор носит
имя Эйлера
Ркр = p2 E Jmin /
l 2 , (1759 г.)
где Ркр - критическая нагрузка, кг; Е - модуль упругости
материала, кг/см2; J min - минимальный центральный
момент инерции площади поперечного сечения стержня, см4; l - длина
стержня, см.
И хотя потеря устойчивости палубных и днищевых связей в результате изгиба корпуса
для деревянных судов была редкостью (ввиду значительных толщин связей и небольшой
длины корпусов), формула эйлеровой силы хорошо послужила инженерам-кораблестроителям
позднее при переходе от деревянных к металлическим конструкциям корпусов, для которых
проблема потери устойчивости связей до сих пор остается актуальной.
События 1759 г.
- Первый русский академик Петербургской АН Михаил Ломоносов (1711-1765 гг.)
заканчивает работу над книгой “Рассуждение о большой точности морского пути”,
в которой предлагает ряд навигационных инструментов и методов астрономического
определения судна в море.
- Английский часовой мастер Джон Гаррисон, после 45-летней упорной работы
над созданием корабельных часов - хронометра, наконец создает вместе со своим
сыном первый надежный хронометр, четвертый по счету, который впоследствии стал
прототипом обычных карманных часов. Это означало практически решение многовековой
проблемы определения долготы, однако только через 13 лет после этого Гаррисон
получит наконец-то свою заслуженную премию.
- Английская эскадра под командованием Джорджа Роднея (1717-1792 гг.) во время
Семилетней войны 1756-1763 гг. блокирует французскую военно-морскую базу Гавр-де-Грас
и уничтожает собранные там морские запасы.
В 1763 г. и затем 1767 г. французский ученый Жан Борда (1733-1799 гг.)
опубликовал сочинение “Опыты по сопротивлению жидкости”, впервые посвященное
экспериментальным исследованиям по сопротивлению воды движению судна. С 1756
по 1757 г. Борда проводил в Дюнкерке эксперименты по буксировке тел в воде (шары,
пластины, конусы и клинья) и установил, что сопротивление тела, полностью погруженного
в воду, пропорционально квадрату скорости, а сопротивление тела, частично погруженного
в воду, растет пропорционально более высоким степеням скорости, ибо они при движении
образуют систему волн.
Необходимо отметить, что серьезные попытки экспериментального определения гидродинамического
сопротивления тел в воде были вызваны, прежде всего, неудовлетворительной точностью
теоретических методов, которые тогда давала гидромеханика. И в дальнейшем, несмотря
на совершенствование последних, экспериментальная гидромеханика продолжает
развиваться параллельно, опираясь на теорию и одновременно дополняя ее, что характерно
для развития технической мысли в целом.
События 1763 г.
- Работа М.Ломоносова над научными трудами, посвященными океанографии и освоению
Северного Ледовитого океана, предвосхитившими многие арктические исследования
XIX и XX веков.
- Русский горный мастер Иван Ползунов (1728-1766 гг.) конструирует первую
в России пароатмосферную промышленную паровую машину.
В 1766 г. в Париже выходит в свет новая книга Эйлера “Полная теория
конструирования и вождения кораблей”, которая помимо обобщения научных исследований
по остойчивости и ходкости судов содержала и некоторые теоретические основы управляемости
парусных кораблей.
К этому времени при исследовании движения тел в пространстве Эйлер впервые использует
подвижную и неподвижную системы координат, связанные между собой углами, которые
впоследствии получат его имя (рис.27). Такой подход при изучении качки корабля оказался
очень удобным и до настоящего времени используется с небольшими изменениями, которые
были внесены в конце XIX века русским ученым-кораблестроителем А.Крыловым, предложившим
использовать корабельные эйлеровы углы.
|
а)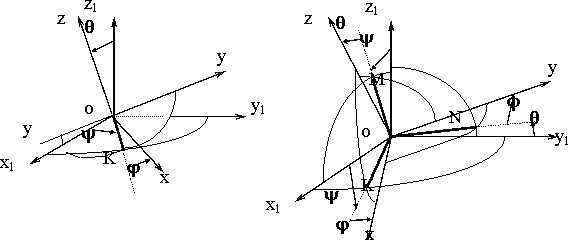 б) б) |
X1OY1 - неподвижная система координат;
XOY - подвижная система координат;
ОК - линия узлов;
y - угол прецессии;
j - угол собственного вращения (относительно
оси OZ);
q - угол нутации.
|
ОК, ОМ, ОN - линии узлов;
XOY - подвижная система координат
(связанная с корпусом судна);
y - угол дифферента;
j - угол рыскания (дрейфа);
q - угол крена.
|
x = cosj cosy
x1 + (sinq cosj
siny - cosq sinj
) y1 + (cosq cosj
siny + sinq sinj
) z1.
Рис.27. Эйлеровы (а) и корабельные (б) углы между подвижной и неподвижной системами
координат и формула перехода по абсциссе.
События 1766 г.
- Русский горный мастер И.Ползунов (1728-1766 гг.) готовит к испытаниям оригинальную
пароатмосферную машину, которая, в отличие от всех предшествующих, позволяла
осуществлять вращательное движение исполнительного механизма.
- Для защиты от древоточцев корпуса английских кораблей в подводной части
оббиваются медными листами в соответствии с приказом Совета Адмиралтейства от
1761 г.
- Повторная попытка русской полярной экспедиции Василия Чичагова (1726-1809
гг.) пройти Сев. морским путем, в результате которой было завершено исследование
района Шпицбергена.
- Первая французская кругосветная экспедиция под командованием выдающегося
мореплавателя и военачальника Луи Бугенвиля (1729-1811 гг.) отправляется в плавание,
которое закончится в 1769 г.
- Вступил в строй флагманский корабль Горацио Нельсона (1758-1805 гг.) - 104-пушечный
линейный корабль “Виктори”, построенный в 1765 г. в Чатаме корабельными мастерами
Д. Локом и Э. Аллином и участвовавший в знаменитом Трафальгарском сражении с
франко-испанским флотом в 1805 г., во время которого прославленный адмирал был
смертельно ранен.
- Гибель русского купца и зверопромышленника, пионера промышленного освоения
Ближних Алеутских островов, Андреяна Толстых на боте “Петр” у берегов Камчатки
после вторичного поиска в Тихом океане таинственной “Земли Хуана да Гамы”.
В 1768 г. издается знаменитый “Атлас архитектуры корабля” известного
в Европе шведского инженера-кораблестроителя и ученого Фредерика Чапмана (1721-1808
гг.). В своей книге Чапман составил подробный атлас конструкций боевых кораблей
разных рангов и предложил “параболический” способ проектирования теоретического
чертежа, где основные линии - шпангоуты и ватерлинии представляли из себя параболы,
а также различные способы вычисления площадей сечений корабля, его водоизмещения,
центра величины и метацентрического радиуса, указал влияние на остойчивость и качку
корабля его ширины и метацентрической высоты, обусловливая величину последней не
более 1,8 м для самых крупных линейных кораблей. При этом ограничение начальной
метацентрической высоты представляет первую попытку нормирования остойчивости крупных
боевых кораблей. За этот капитальный труд, имеющий огромную практическую ценность
для проектирования судов, Чапман был избран членом Стокгольмской академии наук.
 |
Краткая биографическая справка:
Фредерик - Хенрик Чапман, шведский корабельный инженер
и ученый, основоположник теории проектирования судов, вице-адмирал.
Образование получил в Швеции, изучал судостроение в Англии, член Королевской
АН в Стокгольме, автор трудов по судостроению и проектированию судов.
Изобретатель канонерских лодок и специального метода постройки
судов, главный кораблестроитель Швеции, возглавлял работу королевской
верфи, построившей по его методу 10 линейных кораблей, 11 фрегатов и
множество небольших судов.
|
Впоследствии Чапман разработал также весьма сложный геометрический способ расчета
сопротивления корпуса по теоретическому чертежу корпуса корабля на основании серии
систематических испытаний моделей кораблей, проведенных им на глубоком пруду
неподалеку от Карлсруны. Однако главной заслугой Чапмана было то, что он явился
основоположником еще одной новой науки - теории проектирования судов.
События 1768 г.
- Подготовка эскадры Балтийского флота под командованием Григория Спиридова
(1713-1790 гг.) и Д. Эльфингстона к первому средиземноморскому походу для боевых
действий в тылу у Турции во время русско-турецкой войны 1768-1774 гг.
- Завершено плавание в южной части Тихого океана через Магелланов пролив английского
путешественника и мореплавателя Самюэля Уоллиса (1728-1795 гг.), в результате
которого открыты о. Таити, некоторые острова в Туамоту, Гилберта и Маршалловых
островах.
В 1771 г., развивая работы Эйлера по бортовой качке, член Петербургской
академии наук Д. Бернулли опубликовал теорию боковой качки корабля на волнении,
считавшуюся классической на протяжении почти 100 лет. Рассмотрев качку судна, расположенного
лагом (бортом) к набегающей волне, Бернулли включает в дифференциальное уравнение
качки помимо составляющих инерционных и восстанавливающих сил, так называемую,
вынужденную составляющую, зависящую от параметров волны, и объясняет явление
резонанса при совпадении периодов волны tв
и качки судна на тихой воде tс.
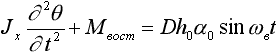 , (1771 г.)
, (1771 г.)
где a o - угол волнового склона,
рад; w в = 2p /tв
- частота волны (1/c); tв - период
волны (с).
В этом же году испанский кораблестроитель Георг Хуан составляет правила,
по которым можно было определить размеры деревянных деталей корпуса и рангоута,
изготовленных из разных пород дерева, сравнивая их с наиболее широко применявшимися
дубовыми деталями. Способ Хуана был основан на гипотезе пропорциональности прочностных
характеристик деревянного материала его весу или плотности. Например, если дубовый
шпангоут следовало заменить новым, изготовленным из другой породы дерева, то удельный
вес дуба надлежало умножить на площадь поперечного сечения детали и, полученный,
таким образом, погонный вес детали поделить на удельный вес нового материала. В
результате получалась площадь поперечного сечения шпангоута из нового деревянного
материала, размеры которого определялись пропорционально старому.
Такой подход в назначении размеров деталей корпуса кораблей говорит о достаточно
высоком уровне испанского судостроения в те времена, о чем свидетельствует, например,
постройка в 1769 г. на Гаванской верфи одного из самых крупных деревянных парусных
боевых кораблей за всю историю судостроения - 144-пушечного линейного корабля “Сантиссима
Тринидад” водоизмещением ок. 5 тыс. т (рис.28). Этот корабль находился в строю испанского
флота вплоть до своей гибели в 1805 г. во время Трафальгарской битвы, где был затоплен
англичанами уже после боя.
Кроме того, в своей книге "Экзамен маритимо", изданной в 1771 г.,
Хуан впервые при оценке сопротивления воды исходит из явления поднятия воды
перед форштевнем и опусканием за ахтерштевнем, а также указывает, что частицы воды
в волне совершают в вертикальной плоскости круговые движения.
События 1771 г.
- Закончилось первое кругосветное плавание выдающегося английского мореплавателя
Джеймса Кука (1728-1779 гг.) на корабле “Индевор”, в результате которого им
открыты о-ва Общества, Большой барьерный риф и доказано островное положение
Новой Зеландии.
- Строительство во Франции Жаном Доксироном (1728-1778 гг.) и Перье бота с
пароатмосферной двухцилиндровой машиной, который через год затонул, не успев
пройти ходовых испытаний.

Рис. 28. Гордость испанского деревянного судостроения - 144-пушечный линейный корабль
“Сантиссима Тринидад” (L =62,4 м, водоизмещение ок. 5 тыс. т).
В 1773 г. французский инженер и физик Шарль Кулон (1736-1806 гг.)
в своих трудах опубликовал правильное решение задачи о нормальных напряжениях при
изгибе балки, которая была развита до современного вида позднее французским ученым
А. Навье, автором первого учебника по сопротивлению материалов.
sz
= Mизг z/ Jy o = Mизг / Wz
, (1773 г.)
где sz - нормальные напряжения в сечении
балки на уровне z от нейтральной (центральной) оси, кг/см2;
Мизг - изгибающий момент балки в рассматриваемом сечении по длине,
кг·см; Wz - момент сопротивления балки на уровне z , см3;
Jy o - центральный момент инерции площади поперечного сечения балки,
см4.
События 1773 г.
- Дж. Кук в поисках Южного материка (Терра Аустралис инкогнита) во время второго
кругосветного плавания на корабле “Резолюшн” впервые в истории мореплавания
пересек Южный полярный круг и дошел до 71°10'ю.ш.
- Французы Ж.Доксирон и Перье на р.Сена успешно испытывают два паровых бота.
- Английский механик Джеймс Уатт (1736-1819 гг.) патентует универсальную паровую
машину двойного действия.
- Изобретатель Ч.Кольз разрабатывает в Филадельфии первый американский паровой
катер.
- Успешные действия Дунайской флотилии под командованием голландского военачальника,
создателя основ морской тактики, Иоганна Кинсбергена (1735-1819 гг.) против
турецкого флота во время русско-турецкой войны 1768-1774 гг.
Примерно в это же время Эйлер получает знаменитые дифференциальные уравнения
движения невязкой жидкости, в основу которых заложен совершенно новый метод исследования
теоретической механики, ориентированный на решение задач динамики не твердого тела
(когда задаваясь начальными значениями времени и координат, определяется траектория
движения материальной точки, а затем ее скорость и ускорение), а жидкости. Он заключается
в том, что внимание наблюдателя фиксируется не на самих частицах жидкости, как это
делается в механике твердого тела, а на точках пространства с заданными координатами,
где и определяются скорости потока в различные моменты времени. Этот метод до сих
пор является основным в гидродинамике, так как позволяет использовать более эффективные
способы и приемы изучения движения различных сплошных сред.
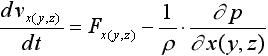 ,
,
где v - скорость жидкости в рассматриваемой точке, м/c; t - время,
с; F - массовая сила, например, вес или инерция, н;
r - плотность жидкости, кг/м3; p -
давление жидкости в рассматриваемой точке, н/м2; x, y,z - направления
по осям координат.
Значительным вкладом Эйлера в развитие гидродинамики является также формулирование
им первого критерия гидродинамического подобия, который представляет собой,
так называемое, число кавитации, используемое при моделировании явления кавитации.
Необходимо отметить, что с проблемой кавитации кораблестроители серьезно столкнутся
только в начале XX века, когда после создания и эксплуатации в качестве судовых
двигателей первых паровых турбин, гребные винты, рассчитанные под низкооборотные
паровые машины и вращаясь с большими оборотами в воде, начнут работать крайне неэффективно
из за кавитации.
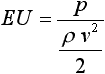 ,
,
где EU - число Эйлера; p - гидростатическое давление
в зоне кавитации, н/м2; r v2/2 - скоростное давление
в зоне кавитации, н/м2.
В ходе разнообразных научных исследований, которые проводил Чапман в 70-х годах
XVIII века, был поставлен и решен основной вопрос теории проектирования судов -
о зависимости водоизмещения и главных размерений
судна от характеристик задания на его
проектирование. В научной работе “Трактат о судостроении”, опубликованной
в 1775 г., а затем и трудах 1806 г., Чапман впервые применил уравнение
масс (нагрузки) в функции водоизмещения и предложил оригинальные способы построения
теоретического чертежа корпуса корабля. При этом связь масс с водоизмещением была
установлена им путем статистического анализа. Чапман попытался также связать
вес полезного груза с водоизмещением судна и его главными размерениями, учитывая
довольно примитивно, и требования остойчивости.
D = S Pi(D) + PНЗ ; (1775 г.)
D = g d LBT = Pгр / hp ,
где D - водоизмещение судна, т; Рi(D) -
зависимые от водоизмещения составляющие нагрузки; РНЗ - независимые
составляющие нагрузки; Ргр - полезная грузоподъемность судна,
т; hp - коэффициент утилизации водоизмещения по грузоподъемности.
Интересной и важной также с точки зрения проектирования является трактовка Чапманом
понятия вместимость судна на основе опыта английского судостроения и судоходства:
“Вместимость наиболее распространенных в Англии видов судов определяется, собственно,
не для того, чтобы можно было по ней узнать, какой груз может принять судно, а для
того, чтобы составить понятие о величине или объеме судна, по которым и производятся
все денежные начисления на судно.
Эту величину находят так: длину киля умножают на ширину судна (по внешней кромке
обшивки), а полученный результат - снова на половину ширины, деленную всегда на
94. Окончательный результат показывает вместимость судна в тоннах.
Если судно приняло большее число тонн, чем получилось при расчете, то говорят,
что оно загружено сверх вместимости; если меньшее, - то говорят, что оно загружено
меньше вместимости” [11].
Так Чапман впервые разъяснил смысл, так называемой, регистровой вместимости
судна как условной разновидности вместимости или объема судна, предназначенной
для начисления портовых налогов.
На основе опытов в бассейне для определения положения шпангоута наибольшего
сечения и отстояния центра величины от миделя Чапман разработал пригодные для
практического применения рекомендации, не противоречащие и современным исследованиям
в этой области.
Опираясь на описании обводов корпуса параболическими формулами, он впервые
составил таблицы с указанием элементов кораблей, спроектированных по его методу
при закономерно изменяющихся полезной нагрузке и других общих проектных характеристиках.
Такие таблицы сегодня рассматривались бы как попытка создания стандартной “сетки”
судов.
Таким образом, научные исследования Чапмана оказали огромное влияние на практику
проектирования судов во всем мире.
События 1775 г.
- На венецианской верфи заложен последний “Буцентавр“ - галера для традиционной
церемонии обручения с Адриатическим морем республики Венеция .
- Французский изобретатель Готье строит паровой бот мощностью 1 л.с. и осуществляет
по Сене показательные плавания.
- Американский изобретатель Бенджамин Франклин испытывает первый водометный
движитель.
Возвращаясь к Эйлеру, нельзя не отметить один из последних его капитальных трудов
в области кораблестроения - однотомное сочинение "Полное умозрение строения и
вождения кораблей, сочиненное в пользу учащихся навигации", изданное в 1776
г. и сконцентрировавшее в себе все самое ценное в практическом отношении, что
давала по тем временам теория корабля. В этом труде, пережившем большое количество
изданий в разных странах, что подтверждает его практическую ценность для кораблестроителей,
рассматривался широкий круг вопросов теории корабля: статика, сопротивление и управляемость,
бортовая и килевая качка судна.
События 1776 г
- Американец Давид Бушнелл (1742-1826 гг.), изобретатель первых морских мин,
на своей металлической подводной лодке с мускульным приводом “Тартл “ осуществляет
атаку английского фрегата "Игл" во время Войны за независимость в Северной Америке
(1775-1783 гг.).
- Дж.Кук на кораблях "Дискавери" и "Резолюшн" отправляется в свою третью и
последнюю экспедицию на Дальний Восток.
Во второй половине XVIII века большой вклад в экспериментальную гидродинамику
вносит французский аббат Шарль Боссю (1730-1814 гг.), проводивший в 1775
г. обширные модельные испытания в г. Мезьере, где на территории инженерной школы
был организован гравитационный бассейн (длина - 30 м, ширина - 16 м, глубина - 2
м, рис.29). Исследованию подверглись различные тела - параллелепипеды, призмы и
цилиндры, имеющие примерную форму корабельного корпуса.
В результате в 1777 г.
в Париже выходит в свет совместный труд Даламбера, Жана Кондорсе (1743-1794
гг.) и Боссю “Новые эксперименты по сопротивлению в жидкостях”, в котором
представлены результаты испытаний этих моделей и впервые обнаружено влияние мелководья
и узкостей на их сопротивление.
 |
Краткая биографическая справка:
Жан Кондорсе, французский философ-просветитель, математик,
социолог, государственный и политический деятель, член и секретарь Парижской
академии наук, член Конвента, реформатор народного образования. |
События 1777 г.
- Один из основателей американских военно-морских сил Поль Джонс (1747-1792
гг.) готовит дерзкое нападение своего корабля на порты Англии во время войны
за независимость в Сев. Америке 1775-1783 гг., которое успешно завершится в
1778 г. уничтожением порта Уитхавен и захватом замка Селкирк.
- Русскими мореходами И.Антипиным, Шабалиным, М.Петушковым и И.Очерединым
закончено исследование Южно-Курильских островов.
Большое значение в конце XVIII века имели научные работы французского инженера
Поля (Пьера) Дюбуа (1734-1809 гг.), который первым попытался связать теоретическую
гидродинамику и практическое судостроение.
Во время работы над своим классическим
трехтомным трудом “Принципы гидравлики”, изданным в 1779, 1786 и 1806
г., и проведения обширных гидравлических испытаний Дюбуа впервые разделил гидродинамическое
сопротивление на сопротивление формы (вихревое) и сопротивление
трения, а также фактически впервые ввел понятие присоединенной массы воды,
отмечая роль кормовой оконечности судна в формировании сопротивления. Но все же
он не смог тогда дать надежных количественных соотношений, которые позволяли бы
вычислить сопротивление судов.

Рис.29. С такого опытового бассейна во французском городке Мезьере начиналась
экспериментальная гидромеханика как жизненно важная составляющая корабельной науки.
События 1779 г.
- Убит в стычке с гавайцами Дж.Кук.
- Корабли английского коммодора Джона Байрона (1723-1786 гг.) по прозвищу
”Джек - скверная погода” разгромили испанскую эскадру у берегов Гренады.
- На заводе Каррона в Шотландии изготовлены новые пушки с небольшой длиной
и очень большим калибром ствола, названные каронадами и поступившие на вооружение
английского флота.
- Франко-испанская эскадра под командованием адмирала Пьера Сюффрена (1726-1788
гг.) блокирует перевозки англичан во время войны за независимость Сев.-Американских
колоний, в результате чего в 1780 г. она перехватила в море 12 купеческих кораблей
с грузами.
- Гренадское морское сражение французской эскадры Ш.д' Эстена (17 кор) после
захвата ей островов Сент-Винсент и Гренада с английской эскадрой Д. Байрона,
закончившееся поражением англичан.
- Бой в Бискайском заливе корабля П.Джонса "Бонхом Ричард" с двумя английскими
кораблями конвойного охранения, считающийся одним из самых ожесточенных сражений
XVIII века: после сдачи одного из английских кораблей, потеряв 150 чел. убитыми,
корабль Джонса, будучи в плачевном состоянии, был покинут командой и затоплен.
В 1782 г. французский математик, астроном и физик Пьер Лаплас (1749-1827
гг.), создавший математическую теорию вероятностей и достигший больших успехов
в области мореходной астрономии, при изучении движения жидкости и других
материальных систем вводит понятие потенциала скорости - условной характеристики
скорости, производная которой по любому направлению дает проекцию скорости на это
направление, и получает уравнение неразрывности безвихревой (потенциальной)
жидкости.
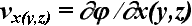 ,
,
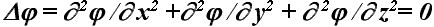 ,
,
где j - потенциал скорости, м2/c;
x,y,z - направления по осям координат; vx(y,z) - проекции
скорости на оси координат, м/c; Dj - оператор
Лапласа.
 |
Краткая биографическая справка:
Пьер Лаплас, французский астроном, математик, физик и
государственный деятель, член Парижской и Петербургской академии наук,
профессор Парижской военной школы, председатель Палаты мер и весов.
Автор классических трудов по теории вероятностей и ошибок, небесной
механики, работ по дифференциальному исчислению и математической физике,
теории капиллярности, теплоте, акустике, геодезии, прочности и пр. Автор
космогонической гипотезы и динамической теории приливов. В разное время
занимал государственные посты министра внутренних дел, вице-председателя
сената, руководителя Бюро долгот.
|
Это уравнение оказалось настолько удачным в математическом моделировании гидродинамических
процессов, что является основным во всех современных гидродинамических теориях,
исследующих многие мореходные свойства судна. В теории потенциального движения невязкой
жидкости, основоположником которой явился Лаплас, основной задачей становится определение
потенциала скорости в рассматриваемой точке, зная который можно определить все кинематические
и динамические параметры исследуемой гидромеханической системы.
События 1782 г.
- Русский механик-самоучка Иван Кулибин (1735-1818 гг.) демонстрирует на Неве
“водоходное судно“, перемещающееся по якорному канату против течения за счет
гребного колеса, вращаемого течением.
- Английская эскадра уничтожает при Алжезирасе испанские плавучие батареи
французского инженера Д.Аркона, спроектированные им как несгораемые от английских
“каленых“ ядер.
- В Херсонском адмиралтействе заложен первый со времен Азовской флотилии корабль
для Черноморского флота - 66-пушечный линейный корабль “ Слава Екатерины”.
- Французский изобретатель Жоффуа Даббан (1751-1832 гг.) начинает оборудовать
паровой машиной бот “ Пироскаф “, который в 1783 г. смог в течении 15 минут
плыть против течения реки Соны.
- Доминиканское (Гваделупское) морское сражение между английской ( Д. Родней,
36 кор) и французской (де Грасс, 30 кор) эскадрами, в ходе которого адмирал
Д. Родней впервые отошел от классических канонов линейной тактики и применил,
так называемую, маневренную тактику линейного боя, разработанную шотландцем
Джоном Клерком (1728-1812 гг.) в научном труде “Движение флотов“.
- В Карлсруне Ф.Чапманом ведется строительство 64-пушечного линейного корабля
“Ретвизан” (D=2200 т, L=49,6 м), который во время русско-шведской войны 1788-1790
гг. был пленен в результате боя с фрегатом “Венус” и линейным кораблем “Изяслав”
и вошел в состав русского Балтийского флота.
В 1784 г. в Дании выходит книга Стиболта “Воздействие на суда усилий
относительно миделя”, которая явилась первой книгой по общей прочности судов.
Стиболт, в отличие от Бугера и Эйлера, не представлял вес корпуса и силы поддержания
в виде аналитических кривых, а использовал фактические данные по конкретному судну.
События 1784 г.
- Основание русским зверопромышленником и купцом Григорием Шелиховым (1747-1795
гг.) первого поселения на берегу Русской Америки.
- Основана главная военно-морская база Черноморского флота Севастополь.
- * В Херсонском адмиралтействе корабельными мастерами Иваном Афанасьевым
(1730-1793 гг.) и И. Соколовым строится флагманский корабль адмирала Ф.Ушакова
“Святой Павел”.
- Английским инженером Генри Кортом запатентован процесс получения пудлингового
железа и прокатки его на вальцах.
- Дж.Уатт успешно испытывает усовершенствованную им в течение 9 лет универсальную
паровую машину двойного действия, признанную с начала XIX века во всем мире
как наиболее удачную и нашедшую применение в качестве надежного судового двигателя.
- Американский изобретатель Дж.Рамси испытывает в присутствии Джоржа Вашингтона
паровую лодку, в качестве движителя в которой использован поршневой водомет.
В 1787 г. во Франции издается книга корабельного инженера В. Клербуа
“Элементарный трактат по конструкции кораблей”, в которой дается описание конструкций
кораблей, их размеры, число и расположение пушек. На основании работ Чапмана, переводом
которых занимался Клербуа, он приводит метод проектирования судов по уравнению нагрузки,
что позволяет еще перед постройкой корабля определить его водоизмещение, положение
центра тяжести и центра величины, метацентрический радиус и высоту.
События 1787 г.
- Севастопольская эскадра Черноморского флота, вышедшая под командованием
М. Войновича после начала русско-турецкой войны 1787-1791 гг. к берегам Болгарии,
на подходе к Варне переносит сильнейший пятидневный шторм, в результате чего
ни в одном сражении она не получала столько и таких серьезных повреждений, как
в этот драматический поход: “Святой Павел” Ф.Ушакова оказался у Кавказского
побережья, фрегат “Крым” пропал без вести, полузатопленную “Марию Магдалину”,
которую снесло к Босфору, захватили турки.
- Американский изобретатель Джон Фитч (1743-1798 гг.) построил второе паровое
судно “Эксперимент“(L=18,3 м) с паровой машиной Уатта и кормовыми веслами, установленными
по идее Бугера, которое показало на испытаниях в 1790 г. невиданную для пароходов
скорость - 12,9 узла.
- Английский заводчик Дж.Уилкинсон строит из железных листов первые цельнометаллические
надводные суда - баржи грузоподъемностью 20 т и длиной 20 м, открывшие эпоху
железного судостроения.
Значительным вкладом в развитие механики твердого тела, и в частности строительной
механики корабля, явилось издание в 1788 г. фундаментального трактата французского
математика Жозефа Лагранжа (1736-1813 гг.) “Аналитическая механика”, в котором
в основу статики он закладывает принцип возможных перемещений, а в основу
динамики - этот же принцип в сочетании с принципом Даламбера. Впоследствии, развивая
эту идею дальше, Лагранж предложил в гидродинамике использовать метод исследования
течения жидкости, который заключается в том, что движение жидкости изучается с позиций
классической теоретической механики: частицы жидкости отождествляют с материальными
точками и определяют траектории их движения, задаваясь в начальный момент времени
начальными координатами. Метод Лагранжа, несмотря на свою значительную трудоемкость,
используется для решения некоторых задач гидромеханики и в настоящее время.
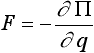 ;
;
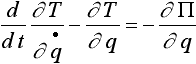 ,
,
где q - обобщенное перемещение; F - обобщенная сила; П -
работа или потенциальная энергия перемещения силы;
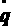 = ¶ q/¶
t - обобщенная скорость; Т - кинетическая энергия системы.
= ¶ q/¶
t - обобщенная скорость; Т - кинетическая энергия системы.
 |
Краткая биографическая справка:
Жозеф Лагранж, французский математик, механик и астроном,
член Берлинской, Петербургской и Парижской академии наук. С 17 лет на
преподавательской работе сначала в военной школе Турина, затем Политехнической
школе в Париже. Создатель Туринской академии. Президент Берлинской академии
наук. Автор трудов по вариационному исчислению координат орбит небесных
тел для навигации, математическому анализу, теории чисел, алгебре,
теории дифференциальных уравнений и теории волн.
|
Cобытия 1788 г.
- Формирование в Средиземном море во время русско-турецкой войны 1787-1791
гг. каперской флотилии под командованием Ламброса Кацониса (1752-1805 гг.),
состоящей из 9 кораблей и одержащей через год ряд побед над турками.
- В южной части Тихого океана пропала без вести вторая французская кругосветная
экспедиция под командованием Жана Лаперуза (1741-1788 гг.), впоследствии обнаруженная
в 20-х годах XIX века на рифах о. Ваникоро ( Санта-Крус ).
- Первое сражение молодого Черноморского флота под командованием М.Войновича
(12 кор) с турецкой эскадрой (Эски-Гасан, 25 кор) у о. Фидониси, закончившееся
поражением турок благодаря командиру линейного корабля “Святой Павел” Федору
Ушакову (1744-1817 гг.). Через два года он будет назначен новым командующим
Черноморским флотом.
- Сражение во время русско-шведской войны 1788-1790 гг. русского флота под
командованием Самуила Грейга (1736-1788 гг.) с шведским флотом при попытке высадки
крупного десанта в районе о.Гогланд, закончившееся полным разгромом шведов.
Успешные действия брига “Меркурий” под командованием Романа Кроуна (1753-1841
гг.), захватившего в крейсерствах 29 судов противника.
- Экспедиция за хлебным деревом английского брига “Баунти", вошедшего в историю
мятежом команды в 1789 г. и беспримерным плаванием на баркасе в Тихом океане
зарвавшегося капитана корабля Вильяма Блая (1754-1817 гг.) с 18 единомышленниками,
который добрался до о.Тимор, преодолев расстояние более 4000 миль (!).
- Успешные действия во время русско-турецкой войны 1787-1791 гг. Днепровской
флотилии под командованием П.Джонса против турецкого флота, закончившиеся взятием
крепости Очаков.
- Испытание в Англии парового судна-катамарана, спроектированного и построенного
шотландцем П.Миллером совместно с горным инженером Вильямом Саймингтоном (1763-1831
гг.).
- Во Франции закладывается самый большой в истории кораблестроения деревянный
парусный боевой корабль - 120-пушечный линейный корабль “Коммерс де Марсель“
(D = 5,3 тыс.т, L=64 м.)
В конце XVIII века Лагранж на базе уравнения Бернулли получает уравнение энергетического
баланса для потока неустановившегося (нестационарного) потенциального или
безвихревого движения жидкости
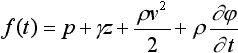 ,
,
где f(t) - функция полного давления жидкости, имеющая в данный момент
времени одинаковое значение для всех точек потока, н/м2;
j - потенциал
скорости потока, м2/c.
В 1795 г. английский исследователь Марк Бофуа (1764-1827 гг.) при
содействии Лондонского общества по усовершенствованию кораблестроения, образованного
как реакция на хроническое отставание английского кораблестроения от французского,
с целью определения сопротивления трения проводит в Гринокском доке самые
крупные в XVIII веке испытания моделей кораблей длиной 12 м (!), продолжавшиеся
в общей сложности 7 лет с 1791 по 1798 г. (всего около 10 тыс. опытов). Эксперименты
Бофуа завершаются изданием в 1834 г., уже после его смерти, капитального труда “Морские
и гидравлические эксперименты”, в котором выявлено влияние на ходкость корабля
обводов носовой, средней и кормовой части корпуса, оценивалась также парусность,
поворотливость и качка исследуемых моделей. При этом он впервые экспериментально
попытался определить величину сопротивления трения, которую все его предшественники,
начиная с Ньютона, считали пренебрежимо малой.
События 1795 г.
- В Бостоне началось строительство из очень твердого белого дуба 44-пушечного
фрегата “Конститьюшн“ для защиты от пиратов американских коммуникаций, который
в настоящее время является самым старым кораблем, постоянно находящемся на плаву
(с 1974 г. - плавучий музей).
- Француз Арман Мезьер разрабатывает проект паровой подводной лодки с весельным
движителем.
Находясь в Париже в конце XVIII века, американец Роберт Фултон (1765-1815
гг.) создал опытовый бассейн длиной 20 м и провел там эксперименты, исследуя
на самоходных моделях эффективность различных типов движителей от гребков
до винтов. В итоге ему удалось сделать то, чего не смогли предшественники: найти
рациональную взаимоувязку корпуса, паровой машины и гребных колес. В 1803 г. первая
экспериментальная паровая лодка Фултона развила скорость 4,8 км/час, двигаясь против
течения Сены.
 |
Краткая биографическая справка:
Роберт Фултон, американский изобретатель, художник и ювелир.
Участник строительства морских каналов, шлюзов и водопроводов. Создатель
различных машин, подводной лодки «Наутиль», плавающей мины, первых коммерческих
пароходов и военного парохода-катамарана – плавучей батареи «Демологос».
|
В 1804 г. издается четвертый и последний том капитального труда русского
профессора второго в Европе (после Парижского) Петербургского Училища корабельной
архитектуры Платона Гамалея (1766-1817 гг.) “Высшая теория морского искусства”,
в котором он развил и существенно дополнил учение Эйлера о теории корабля. И
хотя международного признания этот труд не получил, его следует считать первой капитальной
научной работой, написанной русским ученым-кораблестроителем.
События 1804 г.
- Американский изобретатель Джон Стевенс после испытаний первой в мире паровой
винтовой лодки в 1803 г. патентует гребной винт собственной конструкции, который
устанавливает на катере с паровой машиной Уатта “Литтл Юлиана”, развившим во
время плавания между Нью-Йорком и Хобокеном скорость 5,4 км/ч.
- Успешные испытания на Волге второго “водохода” И.Кулибина, предназначенного
для замены тяжелого бурлацкого труда.
- Американец О. Эванс сконструировал паровой катер для очистки доков Филадельфии.
- Третий год в Индийском океане свирепствует французская каперская эскадра
под командованием Роберта Сюркуфа (1773-1827 гг.), которая только осенью 1806
г. захватила 14 английских кораблей.
- Второй год идет первое кругосветное плавание русских кораблей “Надежда”
и “Нева” 1803 - 1806 гг. под командованием Ивана Крузенштерна (1770-1846 гг.),
которое впервые в истории мореплавания завершится переходом шлюпа “Нева” под
командованием Юрия Лисянского (1773-1837 гг.) из Кантона (Китай) до Британских
островов без заходов в порты.
- Третий год в Шотландии в канале Ферт оф Клайд эксплуатируется наиболее удачный
буксирный пароход своего времени “Шарлотта Дандас” (L=17 м, N=12 л.с.), построенный
инженером В. Саймингтоном. Побывав в свое время на этом судне, Р.Фултон использует
все технические достижения англичан в этой области для создания пароходов нового
поколения, признанных классическими.
- Год находится во французском плену на о.Маврикий английский мореплаватель
Мэтью Флиндерс (1774-1814 гг.), возглавлявший третью английскую экспедицию к
берегам Австралии, где он начинает исследования судового компаса, которые приведут
к открытию им явления девиации от корабельного железа и выработке рекомендаций
по ее устранению.
- Дипломатическая миссия Николая Резанова(1764-1807 гг.) на шлюпе “Надежда”
прибывает в японский порт Нагасаки для проведения переговоров, которые, однако,
закончились безрезультатно.
- Английская армия и флот получают на вооружение гильзы Генри Шрапнеля, начиненные
смертоносными зазубренными осколками.
- Спуск на воду в 1804 г. на Архангельской верфи 74-пушечного линейного корабля
“Сильный”, построенного русским корабельным мастером Андреем Курочкиным (1770-1842
гг.) и признававшегося долгое время образцовым в отечественном кораблестроении.
Входя в состав Средиземноморской эскадры Дмитрия Сенявина, “Сильный” после Лиссабонского
пленения с 1807 по 1813 г. находился в Англии, где его чертежи неоднократно
копировались английскими мастерами, после чего на нем и на линейном корабле
“Мощный” были доставлены в Кронштадт все орудия и снаряды сгнившей сенявинской
эскадры.
В начале XIX века Лаплас вносит свою лепту и в науку о прочности, создав общую
безмоментную теорию тонких оболочек, имеющих форму любого тела вращения (от сферы
до цилиндра) и испытывающих давление изнутри. Уравнение, носящее его имя, в частном
случае дает котельную формулу Мариотта.
Уравнение Лапласа 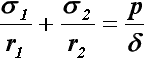 ,
,
где r1 и r2 - соответственно радиусы кривизны параллели
и меридиана поверхности сосуда, м; s 1 и s 2 - нормальные
напряжения растяжения вдоль параллели и меридиана, кг/м2.
Таким образом, Лаплас в целом теоретически обосновывает расчеты прочности тонкостенных*
трубопроводов и резервуаров энергетического оборудования и судовых систем, находящихся
под давлением, что способствовало интенсивному развитию в начале XIX века судовой
энергетики, а затем в конце этого века и различных сложных судовых систем.
В 1822 г. французский ученый Анри (Луи) Навье (1785-1836 гг.),
а позднее, независимо от него, и английский физик и математик Д.Стокс получили
на основе уравнения Эйлера дифференциальные уравнения движения вязкой жидкости и
газа
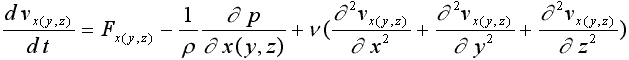 , (1822)
, (1822)
где n = m / r - кинематический коэффициент вязкости жидкости, м2/с.
События 1822 г.
- Английским мореплавателем и путешественником Вильямом Маринером (1790 -
1860 гг.) закончена работа над 3-х томным трудом “Рассказ о туземцах островов
Тонга”.
- Первая попытка русских шлюпов “Открытие” и “Благонамеренный” пройти Сев.
Западным проходом из Тихого в Атлантический океан.
- Первые рейсы первого морского железного парохода “Авраам Мэнби” (L=36 м,
N=80 л.с.), построенного в Англии по проекту заводчика Роберта Нэпира.
- Через 175 лет после открытия Семеном Дежневым пролива между Евразией и Америкой
Колымский отряд экспедиции русского мореплавателя Фердинанда Врангеля (1796-1870
гг.) исследует Сев.-Восточную Сибирь для окончательного решения вопроса о том,
соединяется ли Азия и Америка.
- Французский артиллерист Пэксан конструирует бомбическую пушку большого калибра
(220 мм), стреляющую 80-фунтовой разрывной гранатой.
- Английский пароход “Райсинг Стар” завершил плавание из Грейвсенда в Вальпараисо
(Чили), впервые пройдя с помощью пара Магеллановым проливом.
- Вслед за русской экспедицией Ф. Беллинсгаузена и М.Лазарева 1819 - 1821
гг., открывшей в 1820 г. Антарктиду (Терра Аустралис инкогнита), английский
капитан-китобой Джеймс Уэддел (1787-1834 гг.) на судах “Джейн” и “Буфой” в поисках
новых районов промысла проникает до самой южной из достигнутых в то время широт
в районе Западной Антарктиды.
В 1827 г. английский ученый Традголд опубликовывает первую математическую
теорию гребного винта, позволяющую, несмотря на свою примитивность, аналитически
оценивать эффективность этого нового типа движителя, который уже в 30-х годах XIX
века начнет постепенно вытеснять на морских судах гребные колеса. Однако, практически
все изобретатели гребных винтов того времени все же более охотно шли на экспериментальные
исследования этих движителей, ввиду малой достоверности расчетных способов определения
их характеристик, а также и самого буксировочного сопротивления корпуса.
События 1827 г.
- Наваринский бой объединенного русско-англо-французского флота (11 кор: русская
вторая Архипелагская эскадра Л. Гейдена, английская Э. Кодрингтона и французская
де Риньи) с турецко-египетским флотом под командованием Мухаррем-Бея (36 кор),
закончившийся сокрушительным поражением турков. В этом бою прославился русский
линейный корабль “Азов” под командованием М. Лазарева, который потопил 2 фрегата,
1 корвет, заставил выброситься на берег и затем взорвал 80-пушечный линейный
корабль и уничтожил флагманский линейный корабль, за что ему впервые в истории
русского флота было присвоено звание георгиевского (гвардейского) корабля.
- Английский полярный исследователь Джон Франклин (1786-1847 гг.) на 4 шлюпах
заканчивает обследование арктических берегов Аляски от устья р. Маккензи в западном
направлении.
- Организация первых пароходных сообщений на Черном море из Одессы в Херсон
на транспортном судне “Надежда” и между Одессой, Евпаторией и Ялтой - на пакетботе
“Одесса”.
- В Охотске корабельным инженером Черногубовым построен бриг “Николай”.
- Испытания в Триесте чешским изобретателем Иозефом Ресселем первого в мире
винтового парохода «Циветта» с винтом Архимеда.
В 1832 г. вышел в свет научный труд английского инженера- кораблестроителя
Мак Грегора Лэрда (1808-1861 гг.) по технологии постройки судов из
железа и стали, который является первым научным исследованием, посвященным специфике
сборки металлических корпусов судов. Этот шотландский кораблестроитель известен
также как строитель первого морского стального колесного парохода "Олберка", совершившего
в 1834 г. плавание из Ливерпуля в Гвинейский залив и обратно.
События 1832 г.
- В Монреале идет достройка парохода "Ройал Вильям": среди 235 его акционеров-совладельцев
были Самюэль Кунард, с именем которого связана вся последующая история трансатлантического
судоходства, а также два его брата.
- Основание Шарлем Балем в Париже филиала классификационного общества “Бюро
Веритас”.
В 1833 г. английский физик и математик Джордж Грин (1793-1841 гг.)
получает интегральное уравнение теории потенциала и особые функции, зависящие от
времени и описывающие источники волнообразования единичной интенсивности, на основе
которых впоследствии гидромеханики смогут вычислять волновое сопротивление тел,
движущихся под свободной поверхностью жидкости, и в частности подводных лодок. В
это же время он предпринимает первую попытку математически описать присоединенные
массы воды.
l = ò vr (v/vo)2dV,
(1833 г.)
где l - присоединенная масса воды объемом V вокруг твердого тела, колеблющегося
в жидкости, кг; v - cкорость частицы воды объемом dV, м/c2;
vo - скорость центра массы твердого тела, м/c2.
События 1833 г.
- Командующим Черноморским флотом и портами Черного моря назначен контр-адмирал
Михаил Лазарев (1788-1851 гг.), прослуживший на этих должностях 18 лет и сделавший
огромный вклад в развитие Военно-морского флота и судостроения на Черном море.
- Экспедиция русского Черноморского флота в Босфор по просьбе турецкого султана
Махмуда II для высадки десанта у Стамбула, которая вынудила приостановить наступление
на турецкую столицу египетской армии восставшего паши Мухаммеда Али.
В 1834 г. Регистр английского Ллойда (в 1696 г. кофейня Эдварда Ллойда
опубликовывает первый бюллетень “Новости Ллойда” с информацией о судах, с 1734 г.
“Списки Ллойда” печатаются периодически, в 1760 г. опубликована Регистровая книга
Ллойда и сформировано первое классификационное и страховое общество “Регистр английского
Ллойда”) выпустил “Книгу правил, регламентирующую порядок классификации судов”
(А1 - первый сорт, А2 - второй сорт и т. д.). С тех пор это общество регулярно
выпускает Правила постройки и классификации судов, которые отражают весь
опыт, накопленный английскими кораблестроителями. Для осуществления надзора за постройкой
судов появились штатные специалисты (“сервейеры”), наблюдающие, чтобы суда строились
без отклонений от правил, соблюдение которых являлось условием регистрации и страховки
будущего судна.
В том же 1834 г. английский ученый и кораблестроитель Джон Рассел (1808-1882
гг.) проводит опыты в канале с моделями, а затем осуществляет и опытные буксировки
натурных кораблей: в 1840 г. - брига “Сфинкс” и в 1846 г. - корабля “Пингвин”. Обработав
результаты этих экспериментов, он впервые установил, что сопротивление воды движущемуся
судну зависит от характера создаваемых им волн (рис.30). В отличие от Дюбуа, Рассел
впервые выделяет волновое сопротивление и обращает внимание своих современников
на важность его учета при проектировании кораблей.
События 1834 г.
- Начало арктической экспедиции русского мореплавателя и гидрографа Петра
Пахтусова (1800-1835 гг.) на шхуне “Кротов” и карбасе “Казаков” для исследования
района Новой Земли.
- Опытные стрельбы бомбических пушек во Франции, показавшие огромное разрушительное
действие разрывных гранат.
- Русским военным инженером Карлом Шильдером (1786-1854 гг.) построена первая
русская металлическая подводная лодка, вооруженная миной и ракетами.
- Англичанин С. Хэлл изобретает и патентует поверхностный конденсатор, позволяющий
допускать непрерывную эксплуатацию парового котла.
- Русский физик и электротехник Борис Якоби (1801-1874 гг.), изучая электромагнетизм,
изобрел электродвигатель, который в 1838 г. будет установлен и испытан на небольшом
судне в качестве главного двигателя.
- В Англии построен железный пароход “Гарри Оуэн”, впервые снабженный железными
водонепроницаемыми переборками, делящими корпус на множество отсеков. В одном
из первых рейсов это судно было посажено на мель и не разрушилось, что показало
все преимущества железных корпусов перед деревянными.
- Кораблестроитель Джон Лэрд (1805-1874 гг.), брат М.
Лэрда, строит в США первый
речной стальной колесный пароход “Джон Рэндольф”.
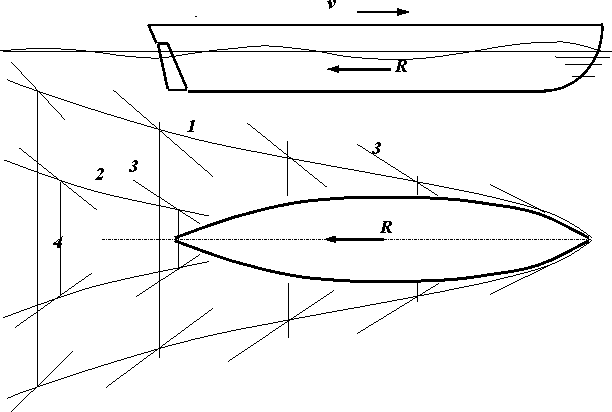
Рис. 30. Виды корабельных волн, возникающих при движении судна в воде. 1 - носовые
расходящиеся волны; 2 - кормовые расходящиеся волны; 3 - линии вершин и впадин расходящихся
волн; 4 - поперечные волны.
В 1835 г. в Англии впервые в мировой практике был принят закон, в соответствии
с которым на каждый фут глубины трюма грузовому судну полагалось иметь 3 дюйма высоты
надводного борта. Это была первая попытка регламентации минимального запаса плавучести
судна для обеспечения его безопасности, являющегося одним из условий обеспечения
такого важного эксплуатационного свойства любого судна как непотопляемость,
хотя она и имела тогда чисто экономические корни.
В те времена стремление судовладельцев взять на борт как можно большее количество
груза и получить, тем самым, максимальный доход с рейса часто заканчивалось трагически
для самого судна и его экипажа. Однако все суда, как правило, и страховались. Поэтому
страховым обществам, наподобие Ллойда, пришлось законодательным образом ограничивать
риск при эксплуатации судов и свои финансовые потери на выплату страховок.
Fmin = k H , (1835 г.)
где Fmin - высота минимального надводного борта; Н - высота борта судна; k - коэффициент пропорциональности между высотой борта (глубиной трюма) и надводным бортом.
Таким образом, при эксплуатации построенных или проектировании новых судов максимальная осадка с точки зрения безопасности могла быть определена как Tmax = H - Fmin= H (1 - k ).
При превышении этого значения осадки вследствие перегруза портовые власти Англии имели право не выпускать грузовое судно в море.
В этом же году в России издан первый научный труд о сопротивлении материалов, применяемых в судостроении, - книга русского корабельного инженера Степана Бурачека
(1800-1876 гг.) “Теория крепости лесов и металлов с приложением к строительству
кораблей”, который можно считать первым учебником по судостроительным конструкционным
материалам. До этого сравнительно молодой инженер уже проявил себя как талантливый
ученый: он усовершенствовал и значительно развил параболический метод построения
теоретического чертежа Чапмана и один из первых в отечественной практике ввел понятие
коэффициентов теоретического чертежа.
 |
Краткая биографическая справка:
Степан Бурачек, русский инженер-кораблестроитель, ученый,
изобретатель, генерал-лейтенант, внесший большой вклад в развитие русского
кораблестроения. Окончил Петербургское училище корабельной архитектуры,
где был оставлен для преподавательской работы. В разное время возглавлял
Астраханское адмиралтейство, проектировал и строил корабли Каспийской
флотилии, осуществлял наблюдение за постройкой военных кораблей «Не
тронь меня», «Аврора», «Кастор» и др., заведовал кафедрой в Офицерском
классе Морского корпуса. Разработчик оригинальной системы набора корпуса,
автор идеи использования твердого топлива методом газификации, одного
из первых проектов подводной лодки и оригинального проекта водотрубного
парового котла, занимался вопросом использования жидкого топлива в судовых котлах.
|
События 1835 г.
- Английский инженер-кораблестроитель Дж.Скотт построил первое металлическое
судно с мощными продольными связями корпуса - стрингерами.
- На Александровском заводе в Петербурге по проекту К. Шильдера построен полуподводный
пароход “Отважный”, способный погружаться несколько ниже уровня воды и оставлять
над водой лишь дымовую трубу.
- Завершение 5-летнего плавания английского брига “Бигл” под командованием
Р. Фицроя, которое считается первой в мире научно-исследовательской экспедицией,
возглавляемой знаменитым Чарльзом Дарвином.
В 1836 г. издается научный труд потомственного судостроителя, русского
корабельного инженера Михаила Окунева (1810-1873 гг.) “Опыт сочинения чертежей
военным судам”, в котором он один из первых рассматривает вопросы проектирования
теоретического чертежа корпуса судна, а также предлагает приближенные формулы для
расчета остойчивости по главным размерениям и коэффициентам полноты, аналогичные
формулам Эйлера. Эта работа явилась значительным вкладом в развитие теории проектирования
судна.
События 1836 г.
- Шведский инженер-кораблестроитель Джон Эриксон (1803-1889 гг.) создает эффективный
гребной винт, который впоследствии стал использоваться на многих американских
винтовых судах.
- Английский фермер Ф. Смит патентует и испытывает на боте винт, который в
1838 г. будет установлен на экспериментальном пароходе “Архимед”, а затем принят
Адмиралтейством как базовый для всех винтовых кораблей.
- В зимнюю Атлантику из Ливерпуля уходит парусник “Даймонд”, который доберется
до Нью-Йорка только через 100 дней (!), в результате чего 17 из 180 пассажиров
умрут от истощения.
- Английский изобретатель Август Зибе работает над совершенствованием водолазного
костюма, оснастив шлем выпускным дыхательным клапаном и приведя его к виду,
в принципе не отличающему это оборудование от современного.
В 1841 г. было произведено первое практическое изучение прочности железных
судов в результате аварии английского судна “Айрон Дюк” (рис.31), севшего
на мель в районе Ярмута.
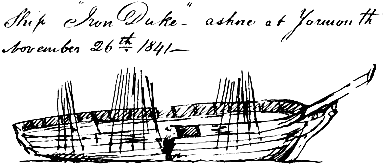
Рис. 31. Эскиз железного корпуса судна “Айрон Дюк”, зарисованный сервейером Регистра
Ллойда Байли при освидетельствовании причин его разрушения.
Сервейер Регистра Ллойда Байли показал расчетным путем, что верхние листы обшивки судна
были слишком тонки для тех усилий, которые там действовали, и что они должны были
на волнении терять свою прямолинейную форму, т.е. устойчивость; это со временем
и привело к появлению в них трещин. Возможно, что именно с “Айрон Дюка” и началось
определение прочных размеров связей металлических судов на основе опыта эксплуатации.
События 1841 г.
- На первую регулярную трансатлантическую линию выходит последний однотипный
с «Британией» четвертый пароход Кунарда – «Колумбия» (ВRT=1150 рег.т, v=10 уз),
который окажется и самым невезучим: в 1843 г. в тумане он налетит на скалы Галифакса
и погибнет.
*) По некоторым
источникам - Изамбарда. |
Во всяком случае, в отличие от деревянной кунардовской «Колумбии», севшей на
мель в 1846 г. у берегов Ирландии и пролежавшая там целый год (!), винтовой пароход
выдающегося английского инженера Исидора* Брунеля (1805-1858
гг.) “Грейт Бритн”, практически не получил повреждений корпуса в результате
его изгиба.
При создании в 50-х годах совместно с Расселом “чуда света XIX века” - гигантского
парохода “Грейт Истерн” ( длина 207,2 м, водоизмещение 32 тыс.т, рис.32)
Брунель, как талантливый инженер и математик, уже применял расчеты элементов конструкции
этого монстра на прочность при общем изгибе корпуса, причем для ее обеспечения он
впервые предлагает стрингерную продольную систему набора корпуса с двойными
дном и бортами, полностью исключающую шпангоуты (!). Эксплуатация этого несчастного
судна (помимо человеческих жертв, которые этот пароход взял при постройке и спуске,
“Грейт Истерн” стал причиной смерти и своего создателя) в течение 30 лет с 1858
по 1888 г. подтвердила правильность выбора конструкции корпуса и не выявила сколько-нибудь
серьезных его пов-реждений. Даже посадка этого гиганта на скалы, в результате которой
он получил пробоину в днище длиной около 25 м, не вызвала у аварийного судна существенного
снижения мореходных качеств.
В 1852 г. немецкий физик Генрих Магнус (1802-1870 гг.), проводя
аэродинамические эксперименты на cнарядах с целью определения влияния их вращения
на траекторию полета, установил эффект, который заключался в том, что при вращении
цилиндра под набегающим потоком на нем образуется боковая сила, направленная в сторону
вращения наветренной части цилиндра (рис.33). Этот эффект, не имеющий на первый
взгляд прямого отношения к судостроению, был позднее успешно реализован при создании
новых парусных судов. В качестве роторного движителя на парусных судах вращающиеся
цилиндры были впервые использованы немецким инженером А.Флеттнером только в середине
20-х годов XX века.
События 1852 г.
- Дж. Эриксон строит первое судно с двигателями Стирлинга, дальнейшее распространение
которые однако не получили.
- Введен в строй французского флота первый в мире парусно-винтовой 90-пушечный
линейный корабль “Наполеон” (D=5047 т), построенный по проекту известного кораблестроителя
Станислава Дюпюи де Лома (1816-1885 гг.) и показавший на ходовых испытаниях
небывалую скорость - 13,5 уз.
- В Бостоне знаменитым американским кораблестроителем Дональдом Мак-Кеем (1810-1880
гг.) завершается постройка самого большого в мире клипера “Грейт Рипаблик” (D=5400
т, L=98,8 м) и не менее знаменитого клипера “Соверин оф Сиз” (L=80,5 м, B=13,4
м).
- Первый трансатлантический рейс немецкого винтового парохода “Эрцгроссгерцог
Фридрих Франц”, построенного в 1851 г. на верфи Тишбайн в Ростоке.
- В Николаеве инженером-кораблестроителем Иваном Дмитриевым (1797-1881 гг.)
строится 84-пушечный линейный корабль “Империатрица Мария”, который, будучи
флагманским кораблем эскадры адмирала Павла Нахимова (1802-1855 гг.), примет
участие в последнем за всю военно-морскую историю сражении парусных флотов в
Синопской бухте в 1853 г., где за 20 минут с помощью бомбических орудий было
уничтожено 15 турецких кораблей и береговые батареи.
- Катастрофа английского пароходо-фрегата “Биркенхед”, которая знаменита неписанным
морским кодексом чести: “Женщины и дети - вперед”. Эта команда капитана Сальмонда
позволила за 20 минут гибели корабля в результате посадки его на камни спасти
всех женщин и детей в составе 184 спасенных из 638 человек, находящихся на борту
судна.
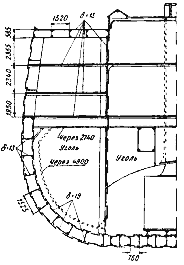

Рис.32. Внешний вид гигантского для своего времени парохода “Грейт Истерн” (L= 207,2
м; B= 25,2 м; T= 9,1 м; v= 13,0 уз; N= 8300 л.с.) и его уникальная конструкция корпуса.
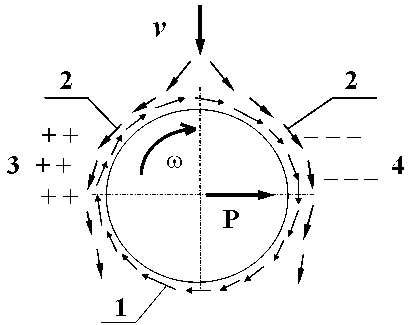
Рис. 33. Схема эффекта Магнуса. 1 - поток пограничного слоя воздуха при вращении
цилиндра; 2 - набегающий поток воздуха; 3 - зона повышенного давления; 4 - зона
пониженного давления.
С 1854 г. в Англии и других странах проводятся исследования по созданию
правил расположения поперечных переборок для обеспечения непотопляемости судов.
В результате к концу XIX века были сформулированы основные требования к разделению
судов на водонепроницаемые отсеки, которые были положены в основу рекомендаций
Первой международной конференции по охране человеческой жизни на море (впоследствии
конвенция SOLAS), организованной после гибели “Титаника” (рис.49) в 1914 г.
События 1854 г.
- Применение французами паровых винтовых бронированных плавучих батарей “Девастасьон”.
“Лав” и “Тоннан” при взятии дунайской крепости Кинбурн.
- Первенец Д.Мак-Кея английский клипер “Молния” на линии Англия - Австралия
показывает среднюю скорость 18 уз, дважды проходя за сутки более 430 миль. Для
английской судоходной компании Блек Болл лайн Д. Мак-Кей завершает строительство
еще трех великолепных клиперов - “Чемпион морей”, “Джеймс Бэнс” и “Дональд Мак-Кей”,
среди которых самым быстроходным оказался “Джеймс Бэнс”: в 1855 г. он дошел
до Австралии за 63 суток и 18 часов, побив все существующие рекорды.
- В канцелярии главного управляющего путями сообщения и публичными заведениями
России графа П. Клейнмихеля пылится рапорт коллежского асессора Иванова с предложением
проекта “трехкильного духоплава” - прообраза судна на воздушной подушке.
- Француз Проспер Пайерн построил подводную лодку “Пиргидростат”, впервые
оснащенную механическим двигателем - паровой машиной.
- Английским путешественником Робертом Мак-Клуром (1807 - 1873 гг.) обследован
последний участок Сев.-Западного прохода из Атлантического в Тихий океан (пролив
Принца Уэльского - пролив Мэлвилла). Оставленное им судно “Инвестигейтор” только
после 57 лет (!) дрейфа вышло на чистую воду.
- Гибель многих кораблей англо-французской эскадры под Балаклавой во время
знаменитого ноябрьского урагана. Среди погибших оказался и английский винтовой
пароход “Принс”, история которого породила легенду о золоте “Черного принца”.
- Героическая оборона под руководством Василия Завойко (1810-1898 гг.) главной
тихоокеанской военно-морской базы Петропавловска-Камчатского от нападения английского
флота и десанта.
- Осада Севастополя англо-французской эскадрой, в результате которой практически
все парусные корабли Черноморского флота были разоружены и затоплены в одной
из его бухт.
- Создан, так называемый, Ливерпульский комитет, который до 1861 г. исследовал
теории и противоположные предложения английских ученых Арчибальда Смита и Джорджа
Эри (1801-1892 гг.) по устранению магнитной девиации компаса.
- Гибель в Северной Атлантике в результате столкновения с французским пароходом
“Веста” одного из четырех шикарных американских трансатлантических лайнеров
компании Драматик лайн, обладателя приза “Голубая лента Атлантики”, парохода
“Арктик”(BRT=2860 рег.т), в результате чего из 365 пассажиров спаслось только
86, причем погибли жена и двое детей самого владельца компании Эдварда Коллинза.
- Пропажа без вести с 480 пассажирами первенца эмигрантской трансатлантической
судоходной компании Инман лайн - одного из первых винтовых лайнеров “Сити оф
Глазго”(BRT=1600 рег.т).
Глава 3c. Период становления и революционного развития корабельной науки (золотой век - по 1906 год)


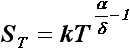 ;
;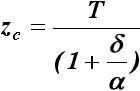 ;
;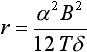 ;
;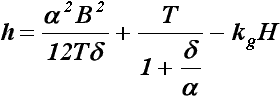 ,
(1749 г.)
,
(1749 г.)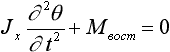
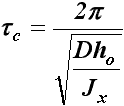

 б)
б)
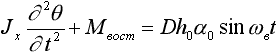 , (1771 г.)
, (1771 г.)
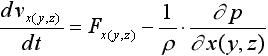 ,
,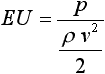 ,
,

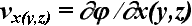 ,
,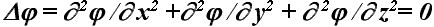 ,
,

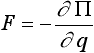 ;
;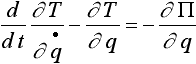 ,
,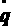 = ¶ q/¶
t - обобщенная скорость; Т - кинетическая энергия системы.
= ¶ q/¶
t - обобщенная скорость; Т - кинетическая энергия системы.
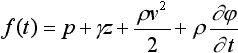 ,
,
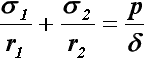 ,
,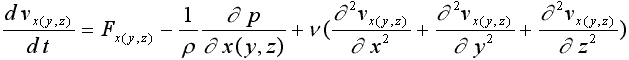 , (1822)
, (1822)