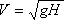, задана точка береговой линии P, которую мы будем отождествлять с населенным пунктом.В настоящей главе описываются некоторые геометрические свойства изолиний полей времен пробега цунами и их разностей от точечных источников в бассейнах простейшей формы, на основании которых строится примерная стратегия анализа размещения сейсмических и уровенных станций СПЦ с позиции достаточной заблаговременности предупреждения о цунами. Это позволяет также создавать более или менее рациональные планы размещения станций измерения уровня океана в условиях реальных акваторий. В общем случае, при достижении данной цели, необходимо учитывать конкретные технические характеристики уровенной станции; затраты на ее установку, а значит, удаленность станции от берега и глубину, на которой она ставится; гидрометеорологические условия района постановки, влияющие на ее живучесть; конфигурацию зоны вероятных источников цунами и, возможно, многие другие факторы. В таком, достаточно полном объеме, задача об оптимальной расстановке уровенных станций (например, в смысле минимизации ущерба от незаблаговременных прогнозов и совокупных затрат на установку и эксплуатацию станций) при произвольной батиметрии становится малодоступной для исследования с помощью математических методов.
По-видимому, следует начинать с максимально упрощенной задачи, чтобы попытаться решить ее аналитически, а, затем уже, учитывая полученные результаты, пытаться обобщать их на более сложные случаи. Такое упрощение достигается здесь за счет перехода к простейшим моделям бассейна (с горизонтальным и наклонным плоским дном) и рассмотрения простейшей задачи об установке одной уровенной станции, обеспечивающей минимальную площадь гидрофизической зоны молчания для одного населенного пункта. Наиболее полно и строго поля времен пробега и разности времен пробега цунами до пары точек, их экстремальные свойства в бассейнах с плоским горизонтальным, наклонным и "полосовым" дном уже проанализированы [Бернштейн, 1992]. Значительная часть приводимых ниже результатов содержится в цитированной работе, и, тем самым, они как бы получают независимое подтверждение. Это позволяет нам описывать их кратко, не углубляясь в достаточно трудные для понимания математические тонкости обсуждаемых задач.
Рассчитывая времена пробега от некоторых точек, мы в то же время получаем информацию о временах добегания цунами до этих точек, что возможно в силу кинематического принципа взаимности , формулировка которого тривиальна: время пробега цунами из точки A (источник) в точку B (приемник) тождественно равно времени пробега из точки B (источник) в точку A (приемник). Это утверждение эквивалентно следующему: фронт волны цунами, соответствующий фиксированному времени пробега T из точки A, как источника, есть геометрическое место таких источников цунами, время добегания волны из которых до точки A равно T.
Менее очевидно, но также справедливо следующее утверждение: разность времен пробега цунами из точек A и B (источники) в точке C (приемник) тождественно равна разности времен добегания цунами в точки A и B (приемники) из точки C (источник). Это эквивалентно утверждению, что изолиния фиксированной разности времен пробега цунами dT от точек A и B представляет собой геометрическое место источников цунами разность времен добегания от которых до точек A и B равна dT. В силу этого утверждения, вычисляя разности времен пробега цунами от выбранной пары точек (источников) мы получаем информацию о разностях времен добегания до этой пары точек (как приемников).
Пусть в плоском бассейне постоянной глубины H, где скорость распространения цунами есть 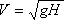, задана точка береговой линии P, которую мы будем отождествлять с населенным пунктом.
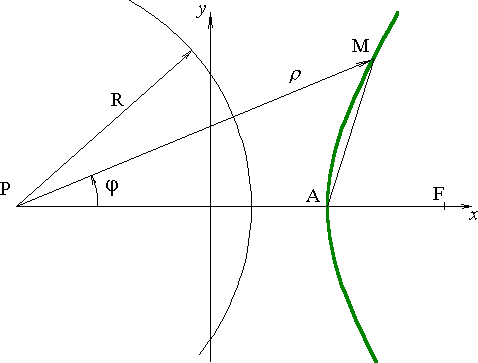
Рис.3. Схема, иллюстрирующая построение границы гидрофизической зоны молчания СПЦ для времени T в окрестности пункта P и станции в точке F в бассейне постоянной глубины.
Предположим для простоты, что минимальная временная дистанция необходимой заблаговременности - Ts=Th=T, тогда сейсмическая зона молчания (см. Главу 1) будет представлять собой часть круга, ограниченного береговой линией, с радиусом R = VT.
Пусть, далее, в точке F (см рис.3) на фиксированном расстоянии L от P установлена гидрофизическая станция. Рассмотрим геометрическое место точек, обладающее тем свойством, что разность времен добегания цунами до населенного пункта P и места установки гидрофизической станции F, от каждой из них есть величина постоянная и равна T. Такое геометрическое место, очевидно, есть гипербола с фокусами в точках P и F, так как постоянство разностей времен добегания T от текущей точки гиперболы до выбранных точек влечет за собой постоянство разности R = VT соответствующих расстояний. Эта гипербола и будет границей гидрофизической зоны молчания СПЦ (состоящей из одной гидрофизической станции в точке F), принадлежащей пункту P.
В декартовой системе координат XOY c центром, расположенным на середине отрезка PF, и осью OX, направленной вдоль него, уравнение рассматриваемой гиперболы примет канонический вид:
x2/a2 - y2/b2 = 1, (2.1)
где
a = VT/2 = R/2,
b2 = c2 - a2, c = L/2, (2.2)
Для частного случая береговой линии, представленной единственной точкой P (маленький остров), поле разностей времен добегания до точек P и F представляется семейством софокусных гипербол с параметром -1 Ј a/cЈ 1.Пример такого семейства показан на рис.4.
Перечислим основные свойства этого семейства, в нашем случае очевидно вытекающие из геометрических свойств гиперболы, но которые по крайней мере частично сохраняются при переходе к более сложным типам формы дна бассейна.
Имеет место пространственная симметрия изолиний разностей времен добегания. Изолинии положительной разности времен добегания до рассматриваемых точек (положим для определенности, что в этом случае точка F - станция - первой фиксирует вступления волны цунами), соответствует изолиния равной по модулю отрицательной разности (когда в пункте P вступление цунами регистрируется раньше чем в F), и это просто две разные ветви одной и той же гиперболы. Ось симметрии (ось Oy на рис.4) одновременно является изолинией нулевой разности времен пробега. При переходе к более сложным формам рельефа дна пространственная симметрия, изолиний разности, конечно, не сохраняется, но остается симметрия самих разностей в бассейне с любым дном.
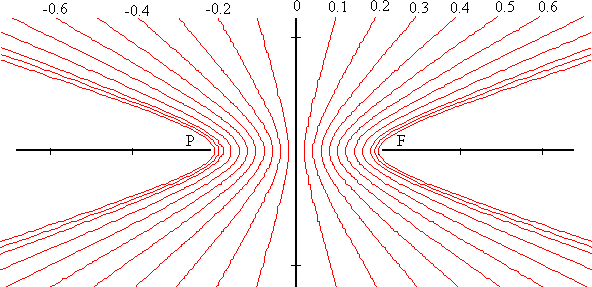
Рис. 4. Изолинии разностей времен пробега от двух фиксированных точек для различных значений параметра a/c пропорционального величине разности времен добегания цунами до точек P и F (формула (2.2)).
Каждая изолиния симметрична также относительно центрального луча, исходящего из F и проходящего через P. Максимальное по модулю значение разности не превышает времени пробега цунами от точки F до точки P, и достигается оно в нашем случае (когда a=±c) для источников, располагающихся на оси OX справа от точки F и слева от точки P вплоть до x®±.Ґ.
В полярной системе системе координат (r, f) с началом в P и полярной осью, проходящей через F, уравнение границы гидрофизической зоны молчания (гиперболы (2.1)) примет следующий вид
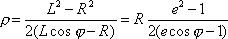(2.3)
где: e = L /R і 1 - эксцентриситет гиперболы.
Когда e = 1 (и, следовательно L=R), ветви гиперболы смыкаются на полярной оси (оси Ox на рис.4), и она вырождается в луч, выходящий из точки F в сторону возрастания, совмещенный с полярной осью. В этом случае заблаговременность T достигается только для источников располагающихся только на этом луче. Поэтому гидрофизическая станция, обеспечивающая прогноз цунами в пункте P с заблаговременностью T или больше, должна устанавливаться за пределами принадлежащей ему сейсмической зоны молчания.
Из формулы (2.3) легко получаем минимальное расстояние от населенного пункта до границы гидрофизической зоны молчания (в (2.3) полагаем f=0)
rmin = R (e + 1) / 2, (2.4)
Из свойств гиперболы (2.1) также следует, что время
Tmax = L /V, (2.5)
составляет максимальную заблаговременность предупреждения о цунами по данным ГФС, установленной на удалении L от населенного пункта, достижимую для источников, находящихся на полярной оси за пределами сейсмической зоны молчания.
Площадь гидрофизической зоны молчания, ограниченная гиперболой (2.1, 2.3) и береговой линией, может быть конечной лишь в случае, если акватория, примыкающая к P, заключается в пределах угла F< p с вершиной в P. Если, при этом, мы устремим точку F к границе сейсмической зоны молчания (это равносильно стремлению эксцентриситета гиперболы (2.1, 2.3) к единице), то указанная площадь будет неограниченно возрастать. Аналогичная картина, очевидно, будет иметь место и при неограниченном удалении точки F от точки P (стремлении расстояния L и эксцентриситета e к бесконечности). Приведенные соображения подсказывают нам, что в пределах рассматриваемой акватории должно существовать положение точки F (положение гидрофизической станции), при котором площадь гидрофизической зоны молчания становится минимальной. Если положить, что возникновение цунами с равной вероятностью возможно в любой точке акватории, то именно при этом (оптимальном) положении уровенной станции вероятность получения в пункте P заблаговременного предупреждения о цунами будет максимальной.
На рис.5 приведены зависимости отношения площади гидрофизической зоны молчания к величине a2 при различных значениях k=tg(Ф/2), указанных на рисунке, от эксцентриситета гиперболы, которые демонстрируют существование вышеупомянутого минимума. Нетрудно видеть, что, при фиксированном значении a, площадь ГЗМ тем больше, чем больше угол F.
Теперь, исходя из вышесказанного, можно строго сформулировать задачу оптимального расположения одной гидрофизической станции по отношению к одному населенному пункту.
В пределах угла F< p с вершиной в точке P отыскать положение фокуса F гиперболы (2.3), обеспечивающее минимум площади криволинейного треугольника, ограниченного сторонами этого угла и гиперболой. Другими словами, требуется отыскать соответствующие (решающие поставленную задачу) направление полярной оси, проходящей через фокус F относительно сторон угла F и положение на ней точки F (расстояние между точками P и F).
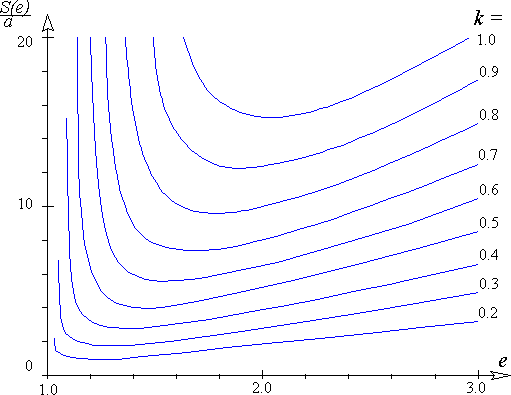
Рис.5. Графики зависимости отношения площади гидрофизической зоны молчания к величине a2 от e = L/R (эксцентриситета гиперболы) и k = tgФ, где Ф - угол с вершиной в населенном пункте P.
Исследование этой задачи было выполнено по нашей просьбе В.А. Терлецким и Н.И. Пекуровой из Иркутского университета для бассейнов с плоским горизонтальным и наклонным дном и этими результатами мы, с глубокой благодарностью, воспользовались в настоящем и следующем разделах. Ими, в частности, строго показано, что, при произвольном фокусном расстоянии L, искомый минимум площади достигается, когда полярная ось координат направлена вдоль биссектрисы угла F.
Наиболее просто аналитическое решение задачи об оптимальном фокусном расстоянии, при симметричном относительно полярной оси сторон угла F, удается получить лишь приближенно, рассматривая вместо криволинейного прямолинейный треугольник PAM (рис.3), площадь которого равна
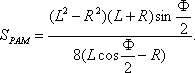(2.6)
Заметим, что S PAM составляет, приближенно, половину площади гидрофизической зоны молчания.
Эта площадь достигает минимума при единственном значении фокусного расстояния
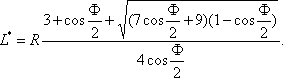(2.7)
Как показывают расчеты на ЭВМ, относительное отклонение приближенного значения L*, вычисленного по формуле (2.6), от истинного, найденного путем численного решения задачи для криволинейного треугольника PAM, находится в пределах 5%, а относительное расхождение площадей соответствующих треугольников не превышает 1%. Это позволяет, при необходимости, использовать соответствующие формулы для оценочных расчетов.
На рис.6 показаны формы границы гидрофизической зоны молчания при трех вариантах расположения станции измерения уровня на биссектрисе угла Ф: на оптимальном расстоянии от P в точке F, на расстоянии, несколько меньшем оптимального, в точке F1, и на расстоянии, несколько большем оптимального, в точке F2. Отрезок гиперболы MM соответствует оптимальному расположению станции. Непоименованный отрезок в верхней полуплоскости чертежа соответствует положению станции в точке F1, а аналогичный отрезок в нижней полуплоскости чертежа соответствует положению станции в точке F2. Знаки + и - указывают, соответственно, на увеличение или уменьшение общей площади ГЗМ при перемещении станции из точки F в точку F1 и F2. Видно, что суммарная площадь при этом увеличивается в обоих случаях.
Анализируя вышеприведенные формулы нетрудно заметить, что площадь гидрофизической зоны молчания, минимальное расстояние от населенного пункта до ее границы, расстояние от пункта до станции растут с ростом Ф. То есть, чем шире раствор угла, вмещающий акваторию, примыкающую к населенному пункту, тем дальше от населенного пункта должна располагаться уровенная станция и тем обширнее будет зона молчания.
Отметим еще раз, что найденный минимум площади ГЗМ достигается при симметричном расположении ее морской границы (гиперболы (2.1, 2.3)) относительно оси OX, а, следовательно, при расположении станции F на этой оси.
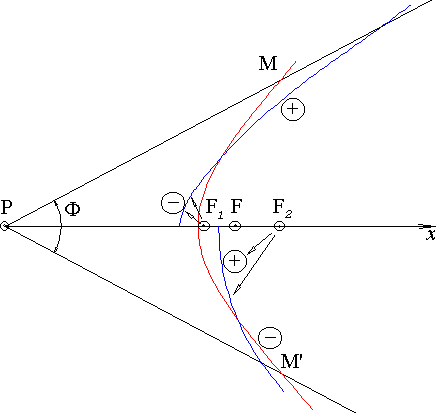
Рис. 6. Форма границы ГЗМ при трех различных положениях уровенной станции в точках F, F1 и F2.
Рассмотрим теперь случай, когда населенный пункт располагается на острове, настолько малом по сравнению с радиусом R сейсмической зоны молчания, что его можно представить в виде точки. Из предыдущего материала следует, что для обеспечения замкнутой зоны молчания вокруг такого острова необходимо не менее трех уровенных станций, чтобы обеспечить выполнение условия Ф < p для каждой из них. Располагая их в вершинах правильного многоугольника (число вершин и сторон такого многоугольника должно быть, очевидно, равно числу станций) с центром в P, на оптимальных расстояниях мы получим замкнутую совместную зону их молчания в виде правильного криволинейного многоугольника с числом сторон, совпадающим с числом станций. Каждая из них минимизирует часть площади зоны молчания в "своем" секторе, где она должна начать регистрацию цунами раньше других. Следовательно, все вместе они должны обеспечить минимальную площадь объединенной зоны молчания при заданном числе станций.
Площадь объединенной ГЗМ при фиксированном времени T и оптимальной установке каждой станции будет тем меньше, чем больше станций участвует в прикрытии пункта, совпадая, в пределе при M ® Ґ, с площадью СЗМ.
Описанный выше простейший пример с использованием многих уровенных станций для прикрытия одного пункта подсказывает нам полезный прием анализа времен добегания цунами и их разностей, реализованный в комплексе программ ANI (см.часть 2).
Пусть tP - время пробега цунами до населенного пункта и tj - времена пробега цунами до каждой из j=1,2,...,M уровенных станций. Как видно из вышеприведенных рассуждений, для построения границы совместной гидрофизической зоны молчания, образуемой этими станциями, для выбранного населенного пункта нет необходимости анализировать все попарные разности времен добегания до них в каждой точке бассейна, а достаточно рассмотреть только одну разность tP-tjmin, где tjmin - минимальное по j=1,2,...,M время для текущей точки бассейна.
Волна от источников из области бассейна, в которой для фиксированного j время tj минимально, будет зарегистрирована на станции j раньше, чем на остальных. Естественно назвать такую область областью минимального времени добегания до станции j или областью (районом) ответственности j-той станции. Вся акватория, таким образом, разделится на M таких областей, по числу станций измерения уровня. В случае бассейна постоянной глубины форма и размеры таких областей определяются только их взаимным расположением. В частном случае расположения станций в вершинах правильного многоугольника с центром в населенном пункте, они будут представлять собой секторы с углом при вершине Ф=2p/M, расходящиеся от населенного пункта, а сами станции будут располагаться на биссектрисах этих секторов.
В реальном бассейне их форма будет определяться также еще и конкретной топографией его дна: чем он глубже в окрестности установки станции j по сравнению с другими, тем обширнее по размерам будет соответствующий район ответственности этой станции при прочих равных условиях. В случае, когда каждая точка его с равной вероятностью может быть источником цунами, легко могут быть выбраны безусловно лучшие места установки уровенных станций из заданной их совокупности. Ими будут те, что имеют наиболее обширные районы ответственности.
Рассуждая подобным образом относительно заданной совокупности населенных пунктов, мы приходим к представлению об областях минимального времени добегания цунами до каждого из них, на которые делится примыкающий к ним реальный бассейн. Населенные пункты, имеющие максимальные площади таких областей могут рассматриваться в качестве возможных мест установки уровенных станций.
Поля времени пробега и разности времен пробега до пары точек в бассейне с плоским наклонным дном, как уже было сказано, строго и очень подробно исследованы в [Бернштейн, 1992]. Здесь мы приводим лишь необходимый минимум сведений, адресуя заинтересованного читателя к цитированной работе.
Рассмотрим бассейн с прямолинейной линией берега, совпадающей с координатной осью OY и плоским наклонным дном, так что глубина воды H=kx и скорость распространения волны цунами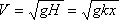 
. Лучи цунами от источника, расположенного в начале координат, представляют собой, как известно [Марчук и др., 1989, В.А. Бернштейн 1992], семейство циклоид с общей начальной точкой (в начале координат), которое может быть представлено в параметрическом виде
x(x) = R (x, t)(1 - cos x), (2.9)
y(x) = R (x, t)(x - sin x),
где: xО[0,2p], t - время пробега волны вдоль луча и R (x, t) - радиус циклоиды. Последний определяется из формулы:
R (x, t) = gkt2/2x2. (2.10)
Фиксируя время пробега t и полагая его равным T - временной дистанции необходимой заблаговременности, получим параметрические уравнения фронта волны (от источника, расположенного в начале координат) и, одновременно, уравнения границы сейсмической зоны молчания для пункта, расположенного в начале координат:
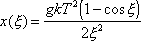, (2.11)
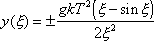
Наиболее удаленная от начала координат точка границы сейсмической зоны молчания находится на оси OX (ось симметрии зоны). Соответствующее расстояние (назовем его «продольным» диаметром) обозначим D1. Максимальный «поперечный» диаметр зоны в направлении, перпендикулярном оси OX обозначим D2. Эти величины равны, соответственно, D1 = gkT2/4, D2 = gkT2/p. Как видно из структуры приведенных выражений, их отношение не зависит ни от параметра бассейна k, ни от параметра фронта T.
В силу трансцендентности выражений для лучей и фронтов, аналитическое выражение для границы гидрофизической зоны молчания - изолинии разностей времен добегания до начала координат и произвольной точки в таком бассейне получено быть не может. Косвенными методами можно установить два главных ее свойства: конечность площади ГЗМ при любом расположении станции относительно населенного пункта на конечном расстоянии от него, и существование единственного минимума этой площади. Указанный минимум достигается при расположении станции на оси OX (оси симметрии сейсмической зоны молчания) на расстоянии от населенного пункта в два раза превышающем "продольный" диаметр сейсмической зоны молчания (независимо от наклона дна k и временной дистанции необходимой заблаговременности T). Площадь ее быстро возрастает при любом смещении станции от этой точки как в обе стороны от оси симметрии так и в сторону берега, и медленно растет при удалении ее от берега. При этом зависимость площади гидрофизической зоны молчания от расстояния между населенным пунктом (началом координат) и уровенной станцией (располагаемой на оси Ox) качественно не отличается от подобной зависимости для плоского бассейна, изображенной на рис.5. А именно, эта площадь стремится к бесконечности, когда уровенная станция находится границе сейсмической зоны молчания, по мере удаления станции от нее, быстро достигает минимума (на расстоянии ~2D1), а, затем, площадь ГЗМ начинает медленно расти.
Задача об оптимальном расположении уровенной станции F относительно пункта P, как уже отмечалось, имеет единственное решение, когда уровенная станция располагается на оси симметрии СЗМ и ГЗМ (на оси Ox, проходящей через населенный пункт P), в обоих рассмотренных случаях бассейна с плоским горизонтальным и наклонным дном. Указанная ось симметрии совпадает с положением центрального луча цунами, выходящего из точки P, обладающего, в частности, тем очевидным свойством, что время добегания цунами вдоль него T(x,y=0) до произвольной точки M(x,y=0) есть minT(x,y) по y. Очевидно, также, что расстояние до границы СЗМ (изохроны T=const) в направлении центрального луча будет максимальным. Эти свойства центрального луча, сохраняющиеся при переходе к бассейнам с более сложной конфигурацией дна, позволяют отыскивать луч, близкий к центральному, при численном моделировании цунами в реальных бассейнах, после чего легко отыскивается методом (небольшого числа) проб оптимальное положение уровенной станции относительно населенного пункта на центральном луче.
Из вышеизложенного материала вытекает ряд очевидных приемов анализа времен добегания цунами до населенных пунктов и станций измерения уровня океана и их попарных разностей.
Основной целью такого анализа является, очевидно, выявление и описание возможных случаев неблагоприятного географического расположения вероятных источников цунами, при которых тревожное сообщение о цунами, выработанное по данным сейсмических или гидрофизических наблюдений, поступит в те или иные населенные пункты заведомо не заблаговременно, что эквивалентно пропуску цунами.
Такие случаи, которые мы далее будем называть неблагоприятной географической ситуацией, когда прогноз цунами выполняется по сейсмическим данным, следует квалифицировать как потенциальные пропуски цунами, и их можно выявить и описать априори, как случаи пересечения цунамигенной зоны и сейсмической зоны молчания того или иного населенного пункта. Следовательно, первое, что необходимо сделать в исследуемой реальной акватории, это построить сейсмические зоны молчания СПЦ для всех существующих и проектируемых прибрежных населенных пунктов и других важных объектов и выделить среди них такие, которые имеют обширные площади пересечения с цунамигенной зоной. Это и будут области вероятных источников цунами, которые неизбежно будут пропущены действующей СПЦ.
Полученная информация может стать основанием для таких изменений конфигурации наблюдательной сети и алгоритма работы сейсмической подсистемы, при которых экономилось бы время, затрачиваемое на регистрацию и обработку записи землетрясения при возникновении неблагоприятной географической ситуации. Ход рассуждений при отыскании наивыгоднейшего (с позиции заблаговременности предупреждения о цунами) положения сейсмической станции примерно следующий. Необходимая длительность регистрации и автоматической обработки землетрясения, будет несколько больше времени пробега до точки регистрации максимума поперечной (поверхностной) волны. Последнее будет минимальным, когда регистрация ведется непосредственно в эпицентре землетрясения. Относительного минимума для населенного пункта, не находящегося в эпицентре, оно будет достигать в при организации регистрации самом населенном пункте. Отсюда вывод: сейсмическая станция должна находиться непосредственно в прикрываемом пункте.
Информация о положении и размерах областей пересечений сейсмических зон молчания с цунамигенной зоной может быть полезной для администрации соответствующих населенных пунктов как побудительный мотив для выработки мер по экономии времени, необходимого для эвакуации населения по тревоге. Наконец, построение сейсмической зоны молчания и выяснение, того, как она соотносится с цунамигенной зоной для мест предполагаемого нового строительства должно стать элементом общей оценки долговременной опасности цунами, которая при этом должна выполняться.
Гидрофизическое прикрытие пунктов, имеющих обширные, пересекающиеся с цунамигенной зоной, районы ответственности, практически бесполезно при близком расположении источников. Однако такие пункты могут оказаться весьма подходящими для установки уровенных станций, прикрывающих другие населенные пункты.
Рациональное размещение уровенных станций для гидрофизического прикрытия пунктов, имеющих относительно небольшие СЗМ в пределах цунамигенной зоны, должно, по возможности, отвечать следующим требованиям: уровненные станции должны находиться в непосредственной близости к возможным эпицентрам цунамигенных землетрясений (то есть в пределах цунамигенной зоны; для подобной постановки существует серьезное ограничение, связанное с опасностью разрушения станции при сильном землетрясении), устанавливаться в наиболее глубоких точках акватории (здесь также существует ограничение, связанное с техническими возможностями такой постановки) или вблизи берегов, располагающихся ближе всего к глубоким ее частям и, при этом они не должны попадать ни в одну из СЗМ прикрываемых населенных пунктов. В любом случае точки, выбранные для размещения уровенных станций, должны иметь, по возможности, максимальные размеры районов ответственности.
В необходимых случаях можно попытаться решить задачу оптимального размещения одной или нескольких уровенных станций для прикрытия одного или нескольких близко расположенных населенных пунктов. Минимизировать при этом необходимо лишь часть площади ГЗМ, попадающую в пределы цунамигенной зоны.
В простейшем случае, когда совместная СЗМ таких пунктов имеет малый по сравнению с характерным размером цунамигенной зоны "продольный" диаметр, а ГЗМ также целиком размещается в ней, можно ограничиться одной уровенной станцией, ее положение следует искать на центральном луче цунами, выходящем из рассматриваемого пункта на расстоянии несколько меньшем двух "продольных" диаметров от него.
Развитие подсистемы наблюдений СПЦ за уровнем моря с целью использования ее данных для оперативного предупреждения о цунами от близких к прикрываемым населенным пунктам источников с позиции достижения необходимой заблаговременности предупреждения имеет смысл лишь в том случае, когда по данным текущих гидрофизических наблюдений можно оперативно осуществить прогноз высоты цунами у конкретных ближайших участков побережья в первые же минуты после начала землетрясения. К этому времени известны только его координаты и магнитуда. Как показано в главе 5, такой прогноз, по-видимому, возможен.